
- •Кафедра тк
- •1. Цель работы
- •2. Выполнение работы
- •2.1. Позиционные звенья
- •2.1.1. Апериодическое (инерционное) звено первого порядка
- •2.1.2. Апериодическое звено второго порядка
- •Временные характеристики
- •Частотные характеристики
- •2.1.3. Колебательное звено второго порядка
- •Временные характеристики
- •Частотные характеристики
- •Весовая (импульсная переходная)
- •Амплитудно-фазовая частотная характеристика
- •2.2. Интегрирующие звенья
- •2.2.1. Идеальное интегрирующее звено
- •Временные характеристики
- •Частотные характеристики
- •2.2.2. Изодромное звено (пропорционально-интегрирующее звено)
- •Временные характеристики
- •Частотные характеристики
- •2.3. Дифференцирующие звенья
- •2.3.1. Реальное дифференцирующее звено
- •Временные характеристики
- •Частотные характеристики
- •2.3.2. Инерционно-форсирующее (реальное форсирующее) звено
- •Временные характеристики
- •Частотные характеристики
- •3. Выводы
Министерство Образования Российской Федерации
Уфимский Государственный Авиационный Технический Университет
Кафедра тк
Отчет по лабораторной работе №1
по предмету «Основы теории управления»
на тему: Исследование характеристик типовых динамических звеньев
Вариант №3
Выполнил:
Проверила:
Уфа 2005
1. Цель работы
Целью работы является изучение временных и частотных характеристик типовых динамических звеньев с использованием автоматизированных средств моделирования на ПК – MATLAB.
2. Выполнение работы
Таблица
|
№ |
Апериод звено |
Апериодич. звено 2 пор. (колеб. звено) |
Интегр звено |
Изодр. звено |
Реальное диф. звено |
Инерц.-форс Звено |
|||||||
|
K |
T [с] |
K |
T [с] |
ξ |
K |
K1 |
K2 |
K |
τ [с] |
K |
T0 [с] |
T [с] |
|
|
3 |
4 |
0,4 |
3 |
0,4 |
2,5 (0,25) |
4 |
4 |
0,8 |
4 |
0,5 |
4 |
4 |
1,5 |
2.1. Позиционные звенья
2.1.1. Апериодическое (инерционное) звено первого порядка
Передаточная функция данного
звена имеет вид
![]() .
.
Временные характеристики
Переходная – получаемая с помощью функции step в MATLAB:
Переходная функция имеет
вид
![]() .
.
Постоянная времени T переходной функции h(t) определяет наклон касательной в начале кривой, т.е. величина T характеризует степень инерционности динамического звена.
Переходная

Весовая (импульсная переходная) - получаемая с помощью функции impulse в MATLAB:
Весовая
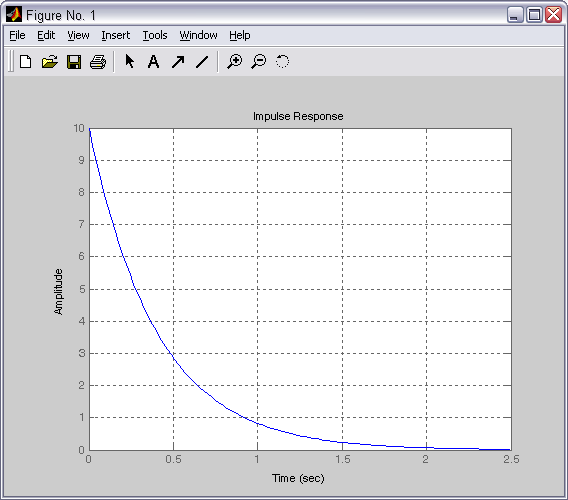
Частотные характеристики
Логарифмическая амплитудная и фазовая частотные характеристики – выполняемые в MATLAB с помощью функции bode:
Логарифмическая амплитудная и фазовая частотные характеристики

Амплитудно-фазовая частотная характеристика – получаемая в MATLAB с помощью функции nyquist.
Амплитудно-фазовая характеристика звена имеет вид:
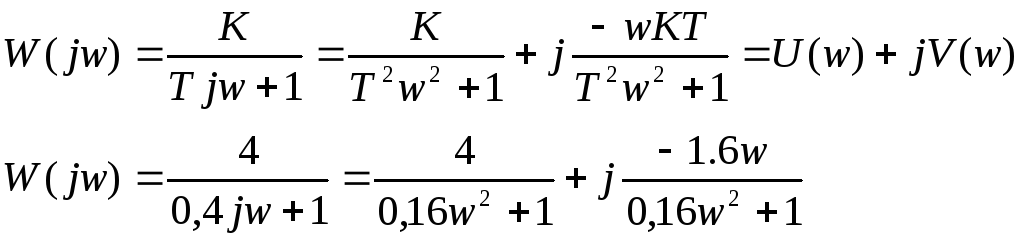
Амплитудно-фазовая частотная характеристика
 Im
Im

 K
K






 Re
Re
w=∞ w=0
 A
A
w
Амплитудно-частотная характеристика имеет вид:
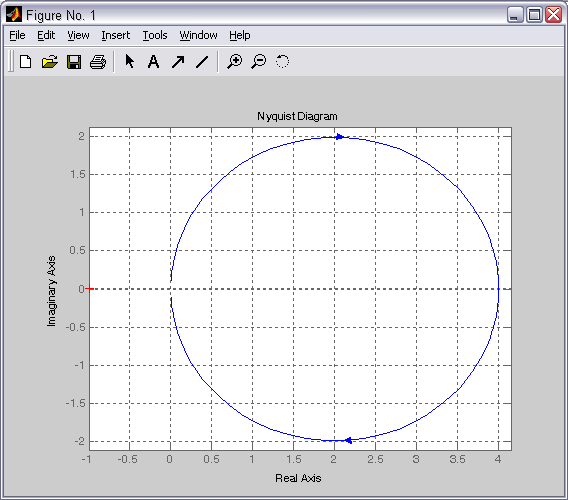
![]()

Фазо-частотная характеристика имеет вид:
![]()


 A
w=1/T
A
w=1/T




 K w,
с-1
K w,
с-1
![]()





 w, с-1
w, с-1 ![]()
 0 w=1/T
0 w=1/T ![]()
2.1.2. Апериодическое звено второго порядка
Передаточная функция звена имеет вид
![]()
![]()
где
![]() - коэффициент затухания.
- коэффициент затухания.
Эта передаточная функция может быть записана также в виде
![]()
где T1
и T2
соответствующие постоянные времени,
определяемые корнями характеристического
уравнения
![]()
Определение корней характеристического уравнения
![]()
![]()
![]()
