1. БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ (ФИЛИАЛ)

2. ГОУ ВПО «САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

3. ФАКУЛЬТЕТ ИНЖЕНЕРНО – СТРОИТЕЛЬНЫЙ

4. КАФЕДРА «УПРАВЛЕНИЕ И ИНФОРМАТИКА В ТЕХНИЧЕСКИХ СИСТЕМАХ

1. ЛАБОРАТОРНАЯ РАБОТА №1

по дисциплине

Теория автоматического управления

ИЗУЧЕНИЕ ГРАФИЧЕСКОЙ ОПЕРАЦИОННОЙ СРЕДЫ СИСТЕМЫ

MATLAB

Вариант 9

Выполнила: ст. гр. УИТ – 32

Вахидова К.Л.

Приняла:

Комлева О.А.

2010

Цель работы: Изучение графической операционной среды системы MATLAB. Получение навыков работы в системе MATLAB при выполнении вычислительных операций.

1. Сформируем из данной системы уравнений матрицу коэффициентов А и матрицу свободных членов В и найдем вектор корней системы уравнений:

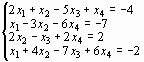
>> A=[2 1 -5 1; 1 -3 0 -6; 2 0 -1 2; 1 4 -7 6]

A =

2 1 -5 1

1 -3 0 -6

2 0 -1 2

1 4 -7 6

>> B=[-4;-7;2;-2]

B =

-4

-7

2

-2

>> x=A\B

x =

3.0588

4.6471

2.8235

-0.6471

Выполним заданные операции с вектором:

>> disp(B')

-4 -7 2 -2

>> disp(B*3)

-12

-21

6

-6

>> disp(B+3)

-1

-4

5

1

>> disp(B.^3)

-64

-343

8

-8

Выполним заданные операции с матрицей:

>> disp(A')

2 1 2 1

1 -3 0 4

-5 0 -1 -7

1 -6 2 6

>> disp(inv(A))

2.8235 -1.6471 -0.5294 -1.9412

5.0588 -3.1176 -1.8235 -3.3529

1.5294 -1.0588 -0.4118 -1.1765

-2.0588 1.1176 0.8235 1.3529

>> disp(A^3)

-37 -45 88 -94

29 -33 117 49

-16 22 -81 -30

-72 -45 57 -166

>> disp(exp(A))

7.3891 2.7183 0.0067 2.7183

2.7183 0.0498 1.0000 0.0025

7.3891 1.0000 0.3679 7.3891

2.7183 54.5982 0.0009 403.4288

>> disp(logm(A))

0.1631 - 1.7841i 0.8871 1.5424i -1.3162 1.1846i

-1.1511 - 5.6696i 0.4401 4.9014i -0.9962 3.7645i

0.0733 - 1.8297i -0.0590 1.5817i 0.6644 1.2149i

1.2662 1.6899i 0.6414 - 1.4609i -1.3746 - 1.1220i

>> disp(sqrtm(A))

1.5408 - 0.5379i 0.1880 0.4650i -1.6135 0.3571i

0.9428 - 1.7092i -0.4930 1.4776i -1.2712 1.1349i

0.7575 - 0.5516i -0.3810 0.4768i 0.7465 0.3662i

0.3163 0.5094i 1.2310 - 0.4404i -1.4339 - 0.3383i

2. Вычислим функции линейной алгебры:

>>X=[2 1 -5 1; 1 -3 0 -6; 2 0 -1 2; 1 4 -7 6]

X =

2 1 -5 1

1 -3 0 -6

2 0 -1 2

1 4 -7 6

>> disp(cond(X))

7.2003

>> disp(norm(X,1))

25

>> disp(norm(X,2))

16.8349

>> disp(rcond(X))

0.0908

>> disp(rank(X))

4

>> disp((det(X)))

1484

>> disp(trace(X))

10

>> disp(null(X))

>> disp(orth(X))

-0.8839 0.4366 0.1449 0.0843

-0.3650 -0.8666 0.2510 0.2295

-0.2586 -0.2298 -0.3882 -0.8542

-0.1364 -0.0744 -0.8748 0.4589

>> disp(rref(X))

1 0 0 0

0 1 0 0

0 0 1 0

0 0 0 1

3. Для вычисления корней полинома сформируем вектор коэффициентов заданного полинома и вычислим корни с помощью функции roots(p):

g(x)=

>> p=[1 1 -17 -45 -100];

>> r=(roots(p))

r =

5.0000

-4.0000

-1.0000 + 2.0000i

-1.0000 - 2.0000i

Для определения коэффициентов полинома воспользуемся функцией poly(r):

>> disp(poly(r))

1.0000 1.0000 -17.0000 -45.0000 -100.0000

Вычислим значение заданного полинома по значению аргумента, используя функцию polyval:

>> disp(polyval(p,3))

-280

Определим значение коэффициентов производной заданного полинома:

>> disp(polyder(p))

4 3 -34 -45

4. Для построения графика заданной функции зададим диапазон изменения аргумента х, запишем заданную функцию и воспользуемся функцией plot:

F(x)=

>> x=0:0.1:10;

>> y=acsch((1-sqr(x))/(1+sqr(x)))-x

>> plot(TH,R),grid

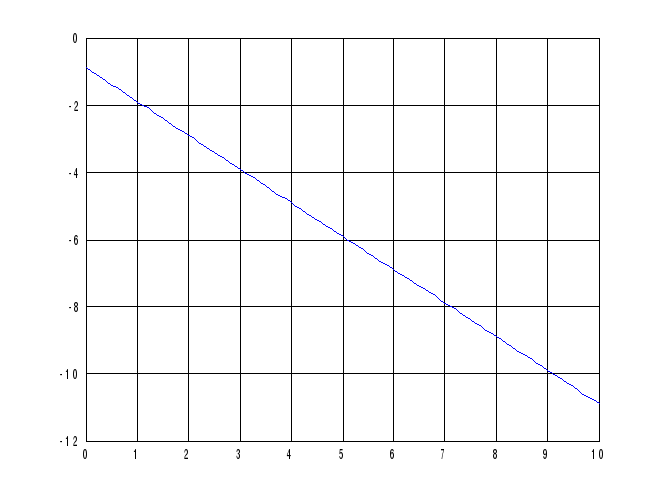
Для построения графика в полярной системе координат необходимо преобразовать декартовые координаты в полярные:

>> x=0:0.1:10;

>> y=acsch((1-x.^2)/(1+x.^2))-x

>> [TH,R] = cart2pol(x,y);

>> plot(TH,R),grid

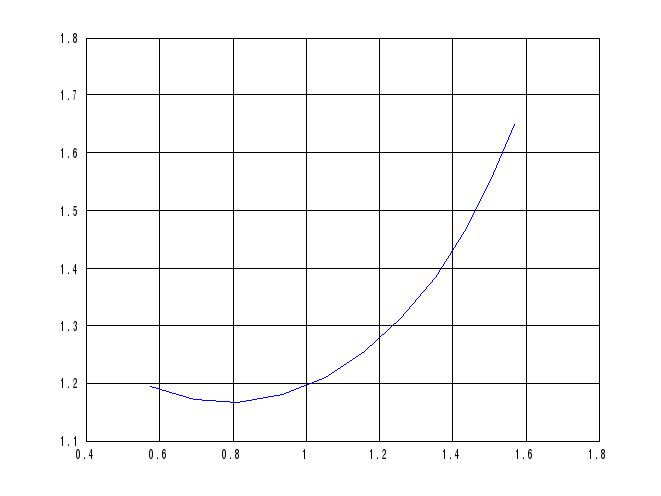
5. Для построения частотных характеристик воспользуемся последовательностью действий:

>> plot(x,y);grid

>> x=0:0.1:1;

>> y=acsch((1-x.^2)/(1+x.^2))-x;

>> [TH,R]=cart2pol(x,y);

>> plot(TH,R),grid

>> P1=[-4 4 -6]; P2=[3 6 1];

>> roots(P1);

>> roots(P2);

>> om0=1e-2; omk=1e2;

>> OM=logspace(-2,2,41); p=i*OM;

>> ch=polyval(P1,p);zn=polyval(P2,p);

>> ACH=abs(ch)./abs(zn);

>> FCH=angle(ch./zn)*180/pi;

>> subplot(2,1,1);

>> loglog(OM,ACH);grid

>> semilogx(OM,FCH); grid

Амплитудно-частотная характеристика передаточной функции

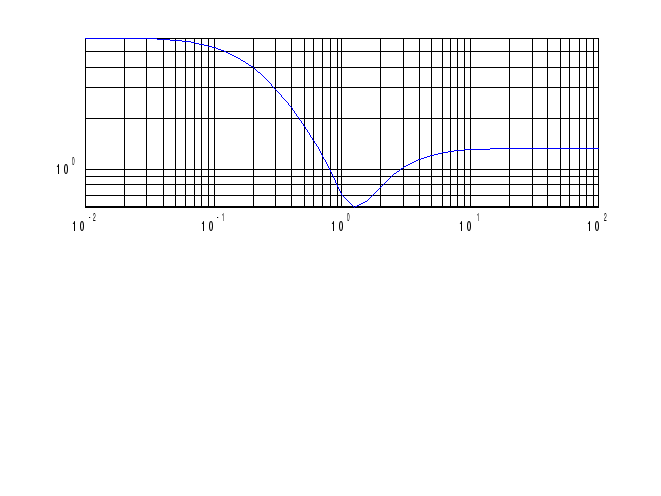
Ф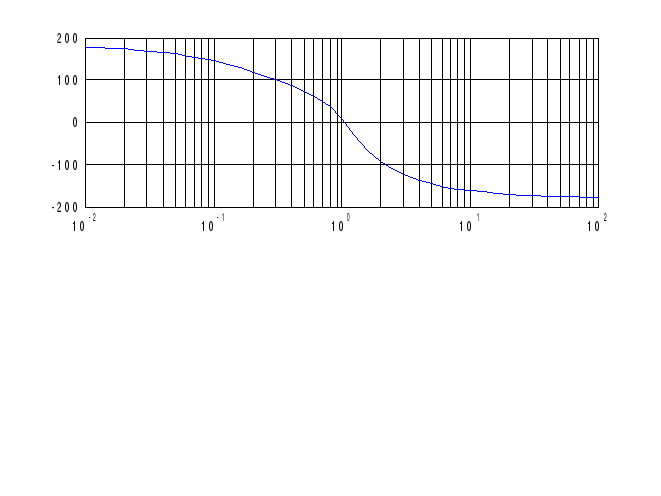 азово-частотная характеристика частотной передаточной функции.