2.3. Дифференцирующие звенья
2.3.1. Реальное дифференцирующее звено
Передаточная функция звена
,
Логарифмическая амплитудная и фазовая частотные характеристики
Изменение параметра K:
>>w= tf([8 0],[0,9 1]);
>> w1=tf([9 0],[0,9 1])
>> w2=tf([10 0],[0,9 1])
>> bode(w,w1,w2)
Изменение параметра τ:
>>w= tf([8 0],[0,9 1]);
>> w1= tf([8 0],[0,8 1]);
>> w2= tf([8 0],[0,7 1]);
>> bode(w,w1,w2)
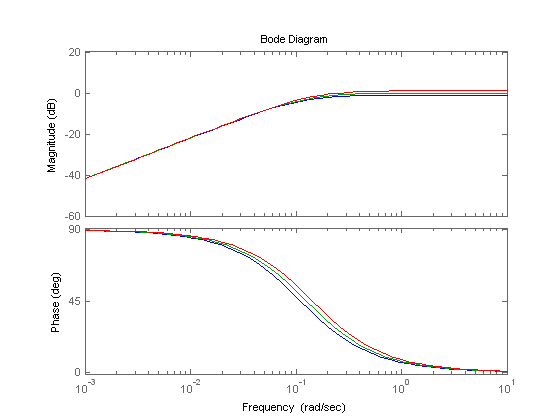
Вывод: Увеличение К приводит к увеличению амплитуды, а увеличение τ приводит к уменьшению частоты и амплитуды.
2.3.2. Инерционно-форсирующее (реальное форсирующее) звено
Передаточная функция звена
(3)
В установившемся режиме выходная величина данного звена пропорциональна входной, т.е. оно может быть отнесено к звеньям позиционного типа.
При η >> 1 оно по своим свойствам приближается к форсирующему звену.
Таким образом, в соответствии с (3) инерционно-форсирующее звено может быть также представлено как последовательное соединение инерционного и форсиру-ющего звеньев.
Логарифмическая амплитудная и фазовая частотные характеристики
Изменение параметра K:
>> w= tf([64 8],[3 1])
>> w1= tf([72 9],[3 1])
>> w2= tf([80 10],[3 1])
>> bode(w,w1,w2)
Изменение параметра T0:
>> w= tf([64 8],[3 1])
>> w1= tf([72 8],[3 1])
>> w2= tf([80 8],[3 1])
>> bode(w,w1,w2)
Изменение параметра T:
>> w= tf([64 8],[3 1]) >> w1= tf([64 8],[4 1]) >> w2= tf([64 8],[5 1]) >> bode(w,w1,w2)
Вывод: Увеличение К и То приводит к увеличению амплитуды, а увеличение Т приводит к уменьшению амплитуды.
1. Как, пользуясь частотными характеристиками, определить параметры (коэффициенты передаточной функции) звена? Пояснить на конкретных примерах.
Интегрирующее звено.
Передаточная функция звена
.
Частотная передаточная функция
Следовательно, АЧХ описывается формулой
ФЧХ строится по формуле
ЛАЧХ апериодического звена 1-го порядка
Из формулы для ЛАЧХ в конкретной
точке на графике ЛАЧХ для частоты 
и соответствующей ей 
можно найти значение 
.
Апериодическое звено первого порядка.
Передаточная функция звена
Частотная передаточная функция
Следовательно, АЧХ описывается формулой
ФЧХ строится по формуле
Из формулы для ФЧХ в конкретной
точке на графике ЛФЧХ для частоты 
и соответствующей ей фазы 
можно найти значение 
.
ЛАЧХ апериодического звена 1-го порядка
Из формулы для ЛАЧХ в той же
точке на графике ЛАЧХ, что и на графике
для ЛФЧХ, для частоты 
вместе с соответствующей этой частоте
и найденным значением 
из предыдущей формулы можно найти
значение 
.
2. Указать особенности построения ЛАХ и ЛФХ динамических звеньев. Что понимается под асимптотической ЛАХ звена?
Логарифмической
амплитудно-частотной характеристикой,
соответствующей передаточной функции
,
называется график функции
от логарифма 
,
где 
– действительная переменная, которая
называется частотой.
Функция 
,
которую получают из передаточной функции
при подстановке в нее 
,
называется частотной
передаточной функцией. Принято
измерять значение ЛАХ в децибелах
(дБ), а значение наклона
ЛАХ – в децибелах на
декаду. Декадой называется
интервал, на котором частота 
меняется в 10 раз. Логарифмической
фазочастотной характеристикой называется
график функции
от логарифма 
.
При ее изображении используется ось
абсцисс, на которой указывают частоту
в логарифмическом масштабе, а по оси
ординат откладывают фазу в дуговых
градусах в линейном масштабе.
Асимптотические ЛАХ звена – это две функции (асимптоты), к которым стремится ЛАЧХ при ω → 0 и при ω → ∞.
3. Как осуществляется построение АФХ динамического звена?
Для построения АФХ динамического
звена обобщенная частотная характеристика
строится на комплексной плоскости в
соответствии с выражением
,когда каждому значению
частоты 
соответствует вектор 
.
При изменении 
от 0 до ∞ конец этого вектора прочерчивает
на комплексной плоскости кривую, которая
будет являться АФХ динамического звена.