8. Определение передаточной функции.

При проектировании САР наряду с методами, основанными на использовании уравнений состояния, часто применяют способы, базирующиеся на представлении элементов (объектов) в виде передаточных функций. Такой подход обладает значительной наглядностью и приводит проектировщика к структурным схемам или графам, с помощью которых можно сложные элементы привести к совокупности простых методами декомпозиции. Для получения передаточных функций линейные дифференциальные уравнения динамических элементов записывают не через оригиналы функций .... 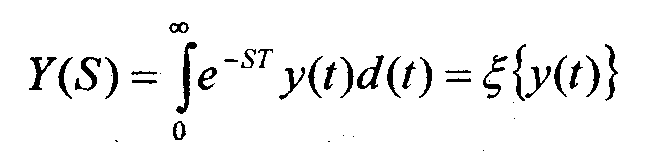при а с помощью прямого преобразования Лапласа приводят к изображениям функций которые записывают прописными буквами в виде

где— символ прямого преобразования Лапласа;— оператор. Наряду с прямым преобразованием Лапласа в теории автоматического регулирования применяют и обратное преобразование Лапласа.

Разностные уравнения записывают в виде последовательности дискретных сигналовили с помощью такта квантованияв видеЕсли применить к этим переменным прямое дискретное преобразование Лапласа, тогда для имеем

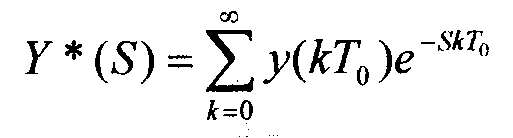
При практическом применении преобразований Лапласа операции ведут не над заданными функциями, а над их изображениями. Для получения изображений необходимо пользоваться некоторыми правилами отображения (свойствами -преобразования). С помощью преобразования Лапласа можно получать ПФ по линейным диф. уравнениям, описывающим динамические процессы в стационарных и нестационарных элементах (объектах). В стационарных элементах коэф-ты явл-ся постоянными, поэтому ПФ постоянна и ее параметры не зависят от времени. В нестационарных элементах коэф-ты меняются от времени и ПФ представляет собой сумму членов ряда, каждый из к-ых опред-ется характером изменения как самого параметра от времени, так и его производных.

9. Критерий устойчивости Михайлова, кривая Михайлова.

При изменении вектор будет своим концом перемещаться по кривой и поворачиваться на некоторый угол. При значенииэтот угол должен быть равен углуКривую геометрического места точек концов вектора называют кривой Михайлова или годографом Михайлова.

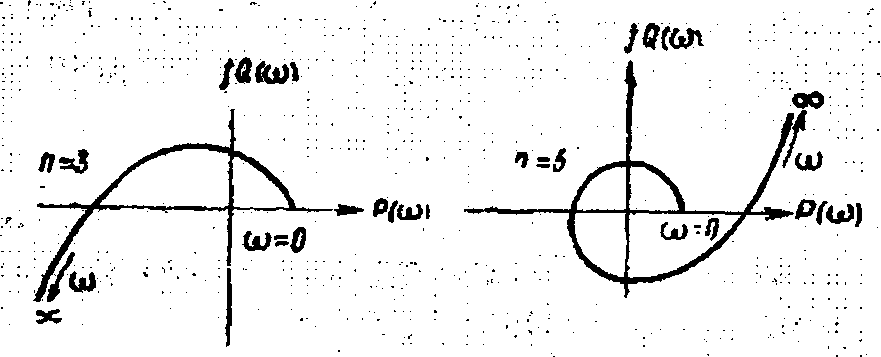Критерий устойчивости, сформулированный А. В. Михайловым: Система автоматического регулирования будет устойчивой, если при изменении от 0 довектор совершит поворот в положительном направлении на угол, равныйгде—степень характеристического уравнения. Для устойчивой системы при измененииобщее число точек пересечения кривой с осями координат равно порядку характеристического уравнения, причем вещественная и мнимая оси пересекаются поочередно. Первой точкой пересечения будет во всех случаях точка, лежащая на положительной вещественной оси. Она получается при значениикогда в выраженииостается только свободный член. Последняя точка пересечения будет для характеристического уравнения четной степени лежать на мнимой оси, а для уравнения нечетной степени —на вещественной оси. В точках пересечения кривой Михайлова с вещественной осью мнимая частьобращается в нуль, и, наоборот, в дочках пересечения кривой с мнимой осью вещественная часть обращается в нуль. Поэтому значенияпри которых пересекается кривая с вещественной или мнимой осью, должны являться корнями уравнений: Функцииможно представить графически. Точки пересечения кривых с осью абсцисс дают значения корней уравнения. Для устойчивости системы необходимым условием являются вещественность и перемежаемость корней уравнений.