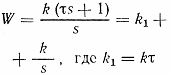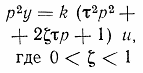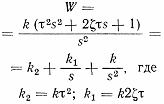8. Лачх и лфчх. Система координат для построения логарифмических характеристик.

ЛАЧХ - Абсциссойлогарифмической амплитудной частотной характеристики являетсячастотав логарифмическом масштабе, поординатеотложенаамплитудавдецибелах. ЛАФЧХ позволяет производить умножение амплитуд простым методом сложения.

ЛФЧХ - Абсциссойлогарифмической фазовой частотной характеристики являетсячастотав логарифмическом масштабе, поординатеотложенафаза. Физически эта диаграмма показывает, на сколько сдвигается фаза сигнала заданной частоты при прохождении его через систему.

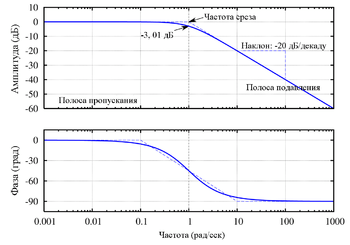
9. Методы построения ЛАЧХ и ЛФЧХ.

После разбиения передаточной функции на элементарные звенья можно построить ЛАФЧХ каждого отдельного звена, а результирующую ЛАФЧХ получить простым сложением.

Аппроксимация ЛАЧХ прямыми линиями

Амплитудная шкала использует масштаб, то есть амплитуда АФЧХ, равная 100 превращается в 40 децибел шкалы ЛАЧХ. Представим передаточную функцию в виде

где— комплексная переменная, которую можно связать с частотой, используя следующую формальную замену:,и— константы, а Н — передаточная функция. Тогда построить ЛАЧХ можно используя следующие правила:

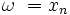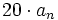• в каждом S, где (нуль), наклон линииувеличивается на дБ на декаду.

• в каждом S, где (полюс), наклон линииуменьшается на 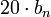дБ на декаду.

• Начальное значение графика можно найти простой подстановкой значения круговой частоты 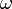в передаточную функцию.

• Начальный наклон графика зависит от числа и порядка нулей и полюсов, которые меньше начального значения частоты. Он может быть найден с помощью первых двух правил.

• В случае комплексно-сопряжённых нулей или полюсов необходимо использовать звенья второго порядка, 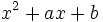, наклон менятся в точке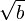сразу надБ на декаду.

Для корректировки ЛАЧХ, аппроксимированную прямыми линиями надо:

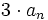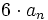• в каждом нуле поставить точку на дБ выше линии (дБ для двух комплексно-сопряжённых нулей),

• в каждом полюсе поставить точку на дБ ниже линии (дБ для двух комплексно-сопряжённых полюсов),

• плавно соединить точки, используя прямые линии в качестве асимптот

Для построения аппроксимированной ЛФЧХиспользуют запись передаточной функции в том же виде, что и для ЛАЧХ:

Основной принцип построения ЛФЧХ — начертить отдельные графики для каждого полюса или нуля, затем сложив их. Настоящая кривая фазы задаётся уравнением

Для того, чтобы нарисовать ЛФЧХ для каждого полюса или нуля, используют следующие правила:

• если 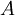положительно, начать линию (с нулевым наклоном) в 0 градусов,

• если отрицательно, начать линию (с нулевым наклоном) в 180 градусов,

• для нуля сделать наклон линии вверх на (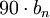для комплексно сопряжённого) градусов на декаду начиная с,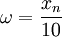

• для полюса наклонить линию вниз на 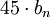(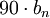для комплексно сопряжённого) градусов на декаду начиная с,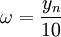

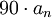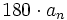• обнулить наклон снова когда фаза изменится на градусов для простого нуля или полюса и наградусов для комплексно-сопряжённого нуля или полюса,

• сложить все линии и нарисовать результирующую.

10. Типовые динамические звенья.

Алгоритмические звенья, которые описываются обыкновенными дифференциальными уравнениями первого и второго порядка, получили название типовых динамических звеньев.

№ (по вопросам)	Тип звена	Дифференциальное уравнение	Перед функцияW=W(S)
11	Идеальное усилительное (безынерционное)	y=ku	W=k
12	Апериодическое (инерционное)	(Tp+1)y= ku
13	Апериодическое (инерционное) второго порядка
14	Колебательное
15	Интегрирующее идеальное	py=ku
16	Интегрирующее инерционное
17	Изодромное
	Изодромное второго порядка
18	Дифференцирующее (ид.)	y=kpu	W=ks
19	Дифференцирующее инерционное
20	Форсирующее