6. Типовые входные воздействия и реакции на них.

Типовые воздействия описываются простыми математическими функциями и легко воспроизводятся при исследовании АСУ. Использование типовых воздействий позволяет унифицировать анализ различных систем и облегчает сравнение их передаточных свойств.

Наибольшее применение в ТАУ находят следующие типовые воздействия:

• ступенчатое;

• импульсное;

• гармоническое;

• линейное.

Ступенчатое воздействие – воздействие, которое мгновенно возрастает от нуля до некоторого значения и далее остается постоянным (рис. 2.2, а).

Ступенчатому воздействию соответствует функция

0 при t 0;

x(t) = а₀ приt 0.

При анализе и расчете систем удобно использовать ступенчатое воздействие, у которого величина а₀ = 1. Его называютединичным ступенчатым воздействием и обозначают1(t). Математическое выражение, описывающее единичное ступенчатое воздействие, имеет вид

0 при t 0;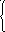

1(t) = 1 приt 0.

Любое неединичное ступенчатое воздействие можно обозначить а₀1(t). Единичное ступенчатое воздействие, возникающее в момент времениt – t1, обозначают1(t – t1).

Импульсное воздействие – одиночный импульс прямоугольной формы (рис. 2.2, б), имеющий достаточно большую высоту и малую длительность (по сравнению с инерционностью испытываемой системы) с площадью а₀.

При математическом анализе АСУ используют единичное импульсное воздействие, описываемое так называемойдельта-функцией

0 при t 0;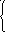

 (t) = приt 0,причём

Последние два выражения позволяют рассматривать дельта-функцию, как импульс, имеющий бесконечно большую высоту, бесконечно малую длительность и единичную площадь. Дельта-функцию можно определить также как производную единичного ступенчатого воздействия:

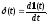
Неединичное импульсное ступенчатое воздействие с площадью а₀ обозначается

x(t) = а₀  (t).

Гармоническое воздействие – сигнал синусоидальной формы, описываемый функцией(рис. 2.2, в)

x(t) = x_m sin t ,(-  t   ),

где x_m – амплитуда сигнала; = 2 / Т – круговая частота;Т – период сигнала.

Гармонический сигнал, начинающий действовать в момент времени t = 0, описывают при помощи единичной ступенчатой функции:

x(t) = 1(t) x_m sin t ,(0 t   ).

Линейное воздействие – воздействие, описываемое функцией (рис. 2.2, г)

x(t) = 1(t) а₁ t ,(0 t   ).

Коэффициент а1 характеризует скорость нарастания воздействия X(t).

Рис. 2.2. Виды типовых воздействий

7. Афчх, ачх и фчх. Комплексная плоскость для построения годографа.

Амплитудная частотная характеристика (АЧХ) – зависимость отношения амплитуд выходного и входного сигналов от частоты

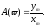
Фазовая частотная характеристика ФЧХ – зависимость фазового сдвига между входным и выходным сигналами от частоты.

ФЧХ показывает, какое отставание или опережение выходного сигнала по фазе создает элемент при различных частотах.

Амплитудную и фазовую характеристики можно объединить в одну общую – амплитудно-фазовую частотную характеристику (АФЧХ). АФЧХ представляет собой функцию комплексного переменногоj:

W(j) = A( ) e ^{j ()} (показательная форма),

где A( )– модуль функции; () – аргумент функции.

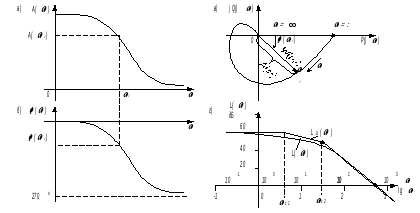
Рис. 2.13. Частотные характеристики:

а – амплитудная; б – фазовая; в – амплитудно-фазовая; г – логарифмическая