Розв’язування

Доцільно порівняти даний ряд із збіжним рядом . Маємо

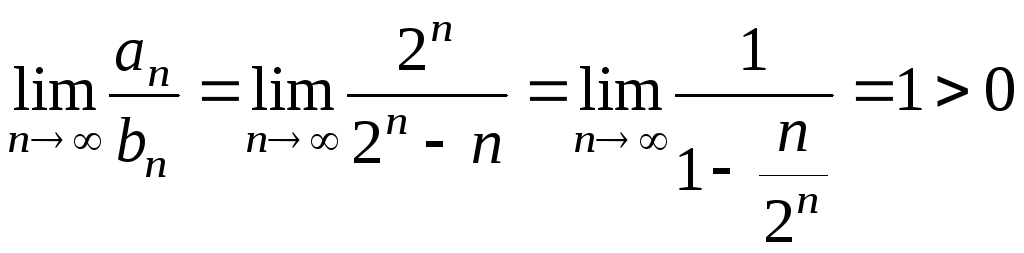
(бо за правилом Лопіталя ) і за теоремою 1.10 даний ряд також збіжний.

Приклад 1.7 Дослідити на збіжність ряд .

Розв’язування

Порівняємо даний ряд з розбіжним гармонічним рядом . Маємо

,

бо . За теоремою 1.10 даний ряд є розбіжним.

Теорема 1.11 (ознака Д’Аламбера). Якщо для додатного ряду існує скінченна границя

, (1.10)

то при даний ряд збіжний, а при - розбіжний.

Доведення

Нехай . Тоді знайдеться додатне число таке, що . Внаслідок рівності (1.10) для всіх значень , починаючи з деякого, виконуватиметься нерівність , а тому

, (1.11)

тобто члени додатного ряду

(1.12)

не перевищують відповідних членів додатного ряду

(1.13)

Оскільки ряд (1.13) збіжний, як геометрична прогресія із знаменником , то ряд (1.12), а з ним і даний ряд , також збіжний.

Якщо , то внаслідок умови (1.10) для всіх значень , починаючи з деякого, виконуватиметься нерівність або . Звідси випливає, що загальний член ряду не прямує до нуля при , і тому ряд буде розбіжним.

Приклад 1.8 Дослідити на збіжність ряд

Розв’язування

Оскільки

,

то за ознакою Д’Аламбера даний ряд збіжний.

Приклад 1.9 Довести збіжність ряду

Доведення

Маємо

,

Границя цього відношення дорівнює 1/2, тобто за ознакою Д’Аламбера ряд збіжний.

Зазначимо, що ознаку Д’Аламбера не можна застосовувати при .

Наприклад, для кожного з рядів . При цьому перший ряд розбіжний, а другий збіжний, оскільки , а ряд – збіжний (див. приклад 1.1).

Теорема 1.11 (гранична ознака Коші). Якщо для додатного ряду існує границя

, (1.14)

то при даний ряд збіжний, а при - розбіжний.

Доведення

Нехай . Тоді знайдеться число таке, що . Внаслідок рівності (1.14) для всіх , починаючи з деякого, виконуватиметься нерівність , тому

.

Тобто члени ряду не перевищують відповідних членів збіжної геометричної прогресії Отже даний ряд збіжний.

Якщо , то внаслідок рівності (1.14), починаючи з деякого , матимемо або . Звідси випливає, що не прямує до 0 при і, отже, даний ряд розбіжний.

Приклад 1.10 Дослідити на збіжність ряд .

Розв’язування

Оскільки

,

то за ознакою Коші даний ряд збіжний.

Приклад 1.11 Дослідити на збіжність ряд .

Розв’язування

Для даного ряду

,

тому питання про його збіжність ознакою Коші не вирішується. Зрозуміло, що цей ряд розбіжний, бо не виконується необхідна ознака збіжності:

.

Теорема 1.12 (інтегральна ознака Коші-Маклорена). Якщо - невід'ємна і незростаюча функція на проміжку , то ряд

(1.15)

і невласний інтеграл

(1.16)

або обидва збіжні або обидва розбіжні.

Доведення

Оскільки функція f(х) незростаюча, то при матимемо . Функція монотонна та інтегровна на відрізку . Почленне інтегрування цих нерівностей у межах від дає

. (1.l7)

Приймаючи в цих нерівностях і додаючи почленно, дістанемо

.

Якщо - частинна сума ряду (1.15), то останні нерівності можна переписати так

і звідки

, (1.18)

. (1.19)

Зауважимо, що послідовність 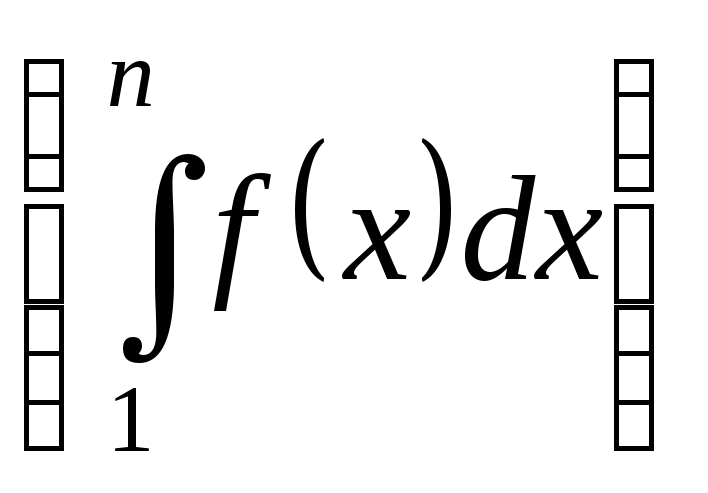неспадна. Справді,

бо .

Нехай невласний інтеграл (1.16) збіжний. Це означає, що існує скінченна границя

, причому .

З нерівності (1.18) одержуємо , тобто частинні суми додатного ряду (1.15) обмежені зверху, і тому ряд (1.15) збіжний.

Нехай тепер невласний інтеграл (1.16) розбіжний. Це означає, що при , а тоді з нерівності (1.19) випливає, що й , тобто ряд (1.15) розбіжний.

Зауваження. Теорема залишається справедливою, якщо функція має вказані властивості для . В ній потрібно лише замінити відповідно на .

Приклад 1.13 Довести, що узагальнений гармонічний ряд

збіжний при , і розбіжний при .