Розв’язування

Дана функція є кусково-гладкою, оскільки вона складається з трьох гладких частин: на , на і на і має дві точки розриву першого роду , . Очевидно, що дана функція абсолютно інтегровна на всій числовій осі, оскільки поза відрізком вона дорівнює нулю, і інтеграл від неї по всій числовій осі зведеться до інтеграла по відрізку .

Таким чином, цю функцію можна подати інтегралом Фур'є; за формулою (3.51) маємо

.

В точках розриву х=0 і ч х=1, одержане подання зберігається, оскільки в цих точках

.

Зокрема, при х=0 одержимо

,

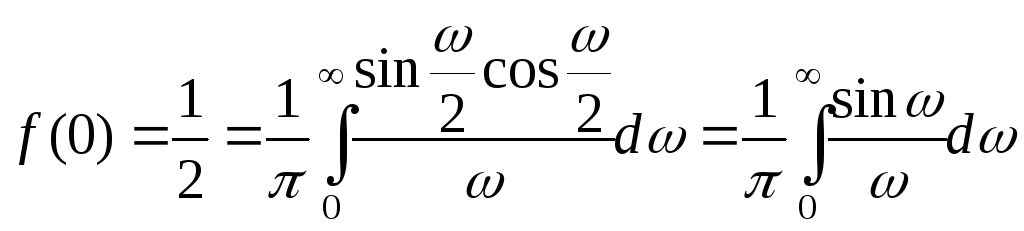що рівносильно рівності

.

Приклад 3.14 Подати інтегралом Фур'є функцію (рис. 3.9)

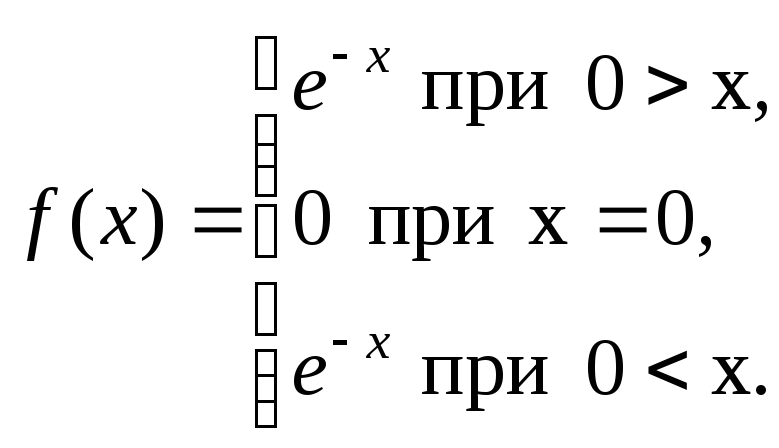
Рисунок 3.9

Розв’язування

Ця функція є кусково-гладкою, оскільки вона складається з двох гладких частин і має один розрив першого роду в точці х=0.

Покажемо, що функція f(х) абсолютно інтегровна на всій числовій осі.

Для цього достатньо показати, що збіжним є інтеграл . Дійсно,

.

Отже, функцію f(x) можна подати інтегралом Фур'є, а оскільки вона є непарною, то можна скористатися формулою (3.58):

.

Інтегруючи частинами, знайдемо внутрішній інтеграл

.

Звідки

.

Таким чином,

.

3.7 Комплексна форма інтеграла Фур’є

Маємо

як інтеграл від непарної функції за змінною із симетричними межами;

як інтеграл від парної функції за змінною .

Запишемо формулу (3.51) у вигляді

Зробивши заміну , одержуємо інтеграл Фур'є в комплексній формі:

, (3.60)

або

. (3.61)

Позначимо

, (3.62)

тоді інтеграл Фур'є запишеться так

. (3.63)

Функцію називають перетворенням Фур'є функції , або, враховуючи фізичні міркування, спектральною щільністю функції . Модуль називається амплітудним спектром функції . Формулу (3.63) називають оберненим перетворенням Фур'є.

Одержані вище формули (3.57) і (3.58) для неперервної функції , у випадку коли вона парна або непарна, можна відповідно записати так:

, (3.64)

де

(3.65)

і

, (3.66)

де

. (3.67)

Функції називаються відповідно косинус- перетворенням і синус-перетворенням Фур'є для даної функції . Рівності (3.64) і (3.66) визначають відповідно обернені косинус- і синус- перетворення.

З рівності (3.62) випливає, .

Приклад 3.15 Знайти спектральну функцію і амплітудний спектр функції

.

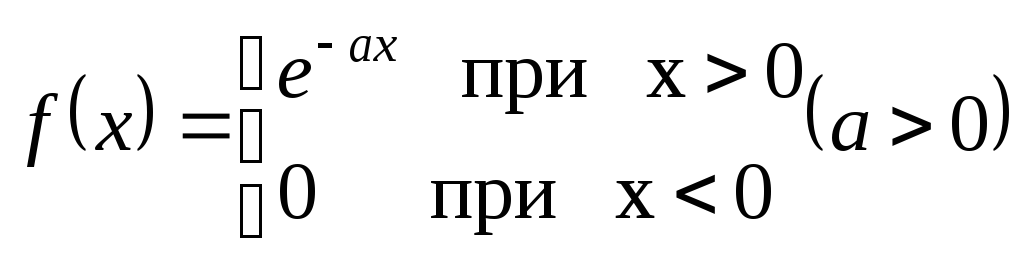Подати комплексною формою ряду Фур'є.

Розв’язування

За формулою (3.62) знаходимо спектральну щільність функції, враховуючи, що при .

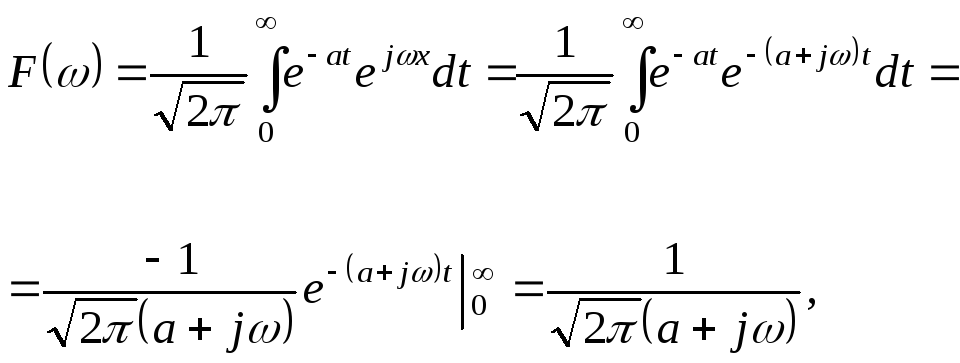
оскільки підстановка верхньої межі дає нуль. Дійсно, за формулами Ейлера маємо:

.

При , внаслідок того що - нескінченно мала функція, а - обмежені функції. Отже, і дійсна, і уявні частини функції прямують до нуля. Це означає, що

Амплітудний спектр

.

Комплексна форма (3.60) інтегралу Фур'є даної функції має вигляд

Рисунок 4

Приклад 3.16 Подати інтегралом Фур'є функцію (прямокутний імпульс)

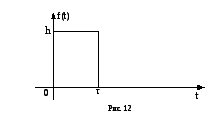
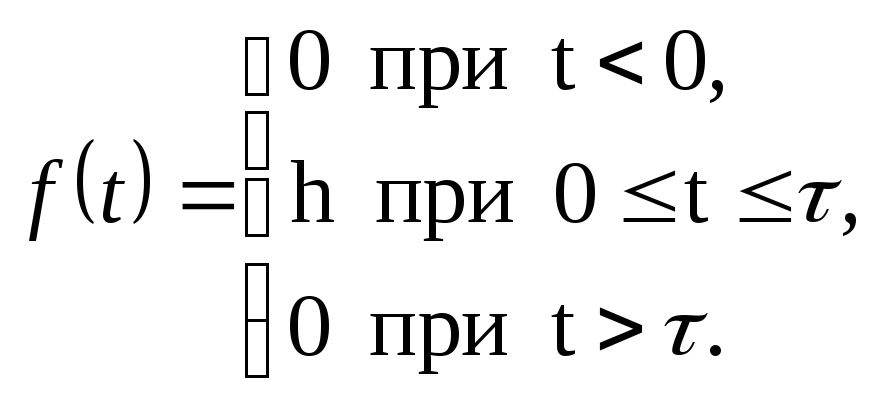
(рис. 3.10).

РРисунок 3.10

Розв’язування

Функція задовольняє всі умови інтегральної теореми Фур'є. Обчислимо спектральну функцію:

Отже, шукане подання матиме вигляд

Виділивши тут дійсну і уявну частини, можна записати одержаний результат в дійсній формі

Приклад 3.17 Розвинути в ряд Фур'є функцію (трикутний імпульс)