Доведення

Нехай . Візьмемо таке , щоб , і . Оскільки ряд збіжний, то при . Отже, знайдеться таке число , що при всіх . Оцінимо загальний член ряду Маємо

,

де . Але при ряд збіжний, бо за ознакою Д’Аламбера при маємо:

Оскільки , то останній результат означає, що ряд збіжний в точці , . За теоремою 2.3 маємо, що ряд збіжний всередині інтервалу збіжності .

Зауваження. Степеневий ряд (2.7) в межах інтервалу збіжності можна диференціювати почленно довільне число раз. При цьому радіуси збіжності всіх рядів, одержаних почленним диференціюванням даного ряду, збігаються з радіусом збіжності вихідного ряду.

Приклад 2.11 Знайти суму ряду

Розв’язування

При даний ряд збіжний. Отже, його можна почленно диференціювати в середині інтервалу збіжності. Позначивши його суму через , маємо

Оскільки , то одержаний ряд похідних як геометрична прогресія із знаменником має суму . Проінтегрувавши ряд

знайдемо його суму:

2.4 Формула і ряд Тейлора

Нехай функція має неперервну похідну в деякому околі точки . Тоді за формулою Ньютона - Лейбніца

.

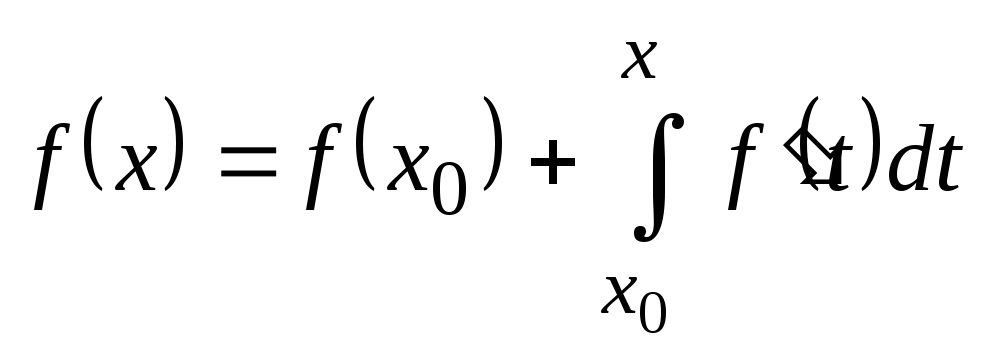Якщо функція має другу неперервну похідну , то за формулою інтегрування частинами

.

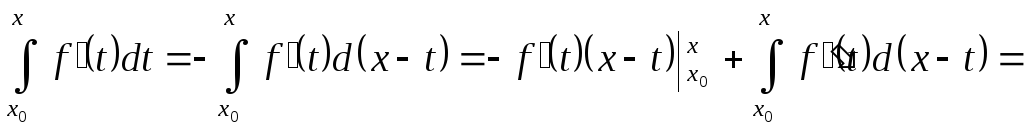
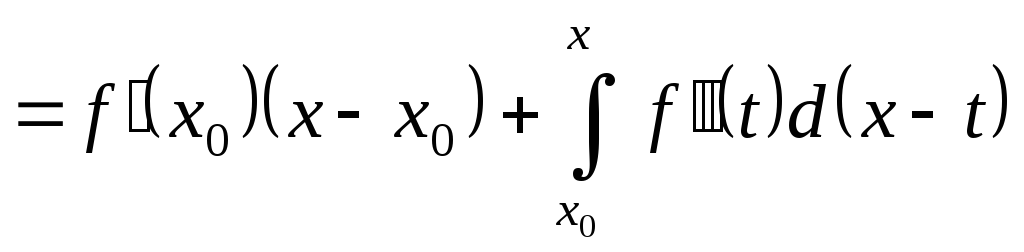Отже,

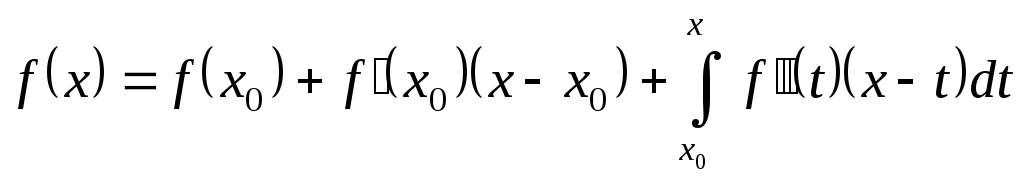
Далі, якщо має третю неперервну похідну , то

і

.

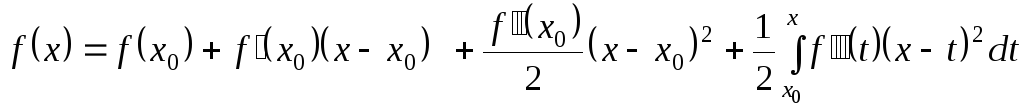Взагалі, якщо має -у неперервну похідну , то

.

Згідно з узагальненою теоремою про середнє, застосованою до інтеграла

,

існує число таке, що

.

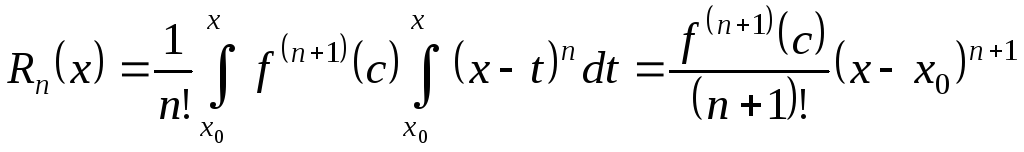Таким чином, має місце теорема.

Теорема 2.7 Якщо функція має неперервну похідну -го порядку в деякому околі точки , то для кожного цього околу існує точка така, що

. (2.10)

Нехай функція має похідні будь-яких порядків в деякому околі точки . Тоді степеневий ряд

(2.11)

називають рядом Тейлора функції в точці .

Для подальшого достатньо буде знайти ряд Тейлора функції в точці , такий ряд називають рядом Маклорена:

(2.12)

Умови розкладу функції в ряд Тейлора дає така теорема.

Теорема 2.8 Якщо функція має похідні будь-яких порядків на відрізку , то на ньому рівність

(2.13)

виконується тоді і тільки тоді, коли залишковий член формули Тейлора

, (2.14)

де , прямує до нуля.

Доведення

Рівність (2.13) еквівалентна рівності

.

Остання рівність, враховуючи (2.14), рівносильна умові

.

Наслідок. Якщо функція має похідні будь-яких порядків на відрізку і всі вони обмежені на ньому , то на відрізку функція розвивається в степеневий ряд:

Доведення

Оскільки функція має похідні довільних порядків на , то для неї можна формально скласти ряд Тейлора (2.11). Доведемо, що він збіжний до . Для цього, за теоремою 2.8, достатньо показати, що залишковий член формули Тейлора

(2.15)

прямує до нуля при . Зауважуємо, що

. (2.16)

Але ряд збіжний, бо за ознакою Д’Аламбера

.

Тому загальний член ряду . З нерівності (2.16) випливає, що при на відрізку .

Зауваження. Можна показати, що якщо функція розкладається в степеневий ряд, то він є рядом Тейлора.

Для спрощення процесу розвинення функцій в ряд Тейлора можна використовувати прикладні пакети Maple та Mathcad (додатки А, В).