Розв’язування

Радіус збіжності знаходимо за першою з формул (2.9)

,

тому

.

Отже, даний ряд збіжний для всіх значень , що належать інтервалу .

Дослідимо поведінку ряду на кінцях проміжку. Підставляючи в даний ряд замість х число 10, одержимо розбіжний гармонічний ряд

При одержуємо числовий знакозмінний ряд

який збіжний умовно.

Таким чином, інтервалом збіжності даного степеневого ряду є пів- відрізок [-1;10).

Приклад 2.9 Знайти інтервал збіжності степеневого ряду

Розв’язування

В даному випадку не можна застосувати формули (2.9) для відшукання радіуса збіжності даного ряду, оскільки він не містить непарних степенів х.

Для відшукання інтервалу збіжності застосуємо безпосередньо ознаку Д’Аламбера. Маємо

.

Отже, ряд збіжний, якщо х² < 2, і розбіжний, якщо х² > 2. Таким чином, . З’ясуємо, чи збіжний даний ряд при х = ± . Підставляючи х = ± , одержуємо числовий ряд , який розбіжний, оскільки його загальний член не прямує до нуля при :

.

Отже, інтервал збіжності даного ряду (-;).

Приклад 2.10 Дослідити на збіжність ряд .

Розв’язування

Застосуємо ознаку Коші, прийнявши . Тоді

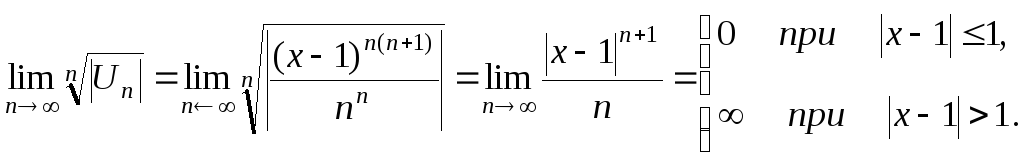
Таким чином, ряд збіжний при , тобто на відрізку [0; 2] .

2.3 Властивості суми степеневого ряду

Теорема 2.3 Степеневий ряд (2.7) збіжний рівномірно на кожному відрізку, що належить інтервалу збіжності.

Доведення

Нехай , де - інтервал збіжності. Доведемо, що на відрізку ряд (2.7) збіжний рівномірно. Візьмемо додатне число таке, що . Тоді для всіх виконуватиметься нерівність , а отже, і нерівність . Але додатний числовий ряд збіжний, оскільки точка , то за ознакою Вейєрштрасса ряд (2.7) збіжний рівномірно на відрізку .

Зауваження. На всьому інтервалі збіжності степеневий ряд може бути збіжний нерівномірно. Наприклад, ряд

на своєму інтервалі збіжності є збіжним нерівномірно, бо нерівність не може виконуватися для

при жодному сталому (адже ).

Теорема 2.4 Сума степеневого ряду (2.7) всередині інтервалу збіжності є функція неперервна.

Доведення

Щоб довести неперервність суми степеневого ряду всередині його інтервалу збіжності, досить довести неперервність цієї суми в довільній точці цього інтервалу. Але точку завжди можна включити всередину деякого відрізка , який повністю міститься всередині інтервалу збіжності. Оскільки на відрізку внаслідок теореми 2.3 ряд (2.7) збіжний рівномірно, а його члени є неперервні функції на цьому відрізку, то за властивістю рівномірно збіжних рядів сума степеневого ряду (2.7) неперервна в точці .

Теорема 2.5 Степеневий ряд (2.7) можна почленно інтегрувати на кожному відрізку , що належить інтервалу збіжності :

,

зокрема

для кожного .

Доведення

Степеневий ряд (2.7) складається з неперервних функцій, тому його можна почленно інтегрувати на відрізках рівномірної збіжності. Яка б не була точка , її завжди можна включити всередину деякого відрізка , який повністю міститься всередині інтервалу збіжності і містить початок координат. Інтегруючи на цьому відрізку в межах від 0 до х ряд (2.7) почленно, дістанемо рівність

Зауваження. Можна показати, що теорема 2.5 залишається справедливою і у випадку, коли числа (обидва чи одне з них) збігаються з кінцями інтервалу збіжності, якщо тільки ряд (2.7) збіжний у відповідних кінцях.

Теорема 2.6 Степеневий ряд (2.7) можна диференціювати почленно у внутрішніх точках його інтервалу збіжності, тобто якщо

,

то

при .