
- •Тема 1 рівняння математичної фізики 6
- •Тема 2 зведення рівнянь другого порядку до канонічного вигляду за допомогою заміни змінних 28
- •Тема 3 метод фур'є 55
- •Тема 4 метод сіток для рівняння параболічного типу 111
- •Тема 5 спеціальні функції математичної фізики 121
- •Передмова
- •Тема 1 рівняння математичної фізики
- •1.1 Рівняння малих поперечних коливань струни
- •1.2 Рівняння малих поздовжніх коливань стержня
- •1.3 Рівняння малих поперечних коливань мембрани
- •1.4 Телеграфне рівняння
- •1.5 Рівняння теплопровідності
- •1.6 Рівняння поширення тепла в стержні
- •1.7 Основні рівняння математичної фізики
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 2 зведення рівнянь другого порядку до канонічного вигляду за допомогою заміни змінних
- •Розв’язування
- •Розв’язування
- •2.1 Рівняння гіперболічного типу
- •Розв’язування
- •2.2 Рівняння еліптичного типу
- •Розв’язування
- •2.3 Рівняння параболічного типу
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •2.4 Розв’язування задачі Коші для рівняння коливання струни методом характеристик (формула д’Аламбера)
- •Розв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 3 метод фур'є
- •3.1 Розв’язання методом Фур’є першої крайової задачі для рівняння малих поперечних коливань струни
- •3.2 Розв’язання методом Фур’є першої крайової задачі для рівняння теплопровідності
- •3.3 Розв’язання методом Фур’є першої крайової задачі для рівняння поширення тепла у нескінченному стержні
- •3.4 Приклади розв’язання задачі Коші для рівняння теплопровідності
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Розв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 4 метод сіток для рівняння параболічного типу
- •Розв’язування
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Тема 5 спеціальні функції математичної фізики
- •5.1 Інтеграл Ейлера першого роду
- •5.2 Інтеграл Ейлера другого роду
- •5.3 Функція Бесселя
- •5.4 Рекурентні формули для функції Бесселя
- •5.5 Інтегральне представлення Пуассона функції Бесселя та його використання
- •5.6 Сферичні функції. Поліноми Лежандра
- •5.7 Виробнича функція для поліномів Лежандра
- •5.8 Рекурентні формули для поліномів Лежандра
- •Питання для самоперевірки
- •Завдання для самостійної роботи
- •Відповіді
- •Література
- •Предметний покажчик
Питання для самоперевірки
-
Які функції називається спеціальними? Наведіть приклади спеціальних функцій.
-
Сформулюйте визначення бета-функції за допомогою невласного інтеграла.
-
Перерахуйте основні властивості бета-функції.
-
Дайте означення гамма-функції та запишіть формулу, що пов’язує бета - та гамма-функції.
-
Перерахуйте основні властивості гамма-функції.
-
Запишіть рівняння Бесселя індексу
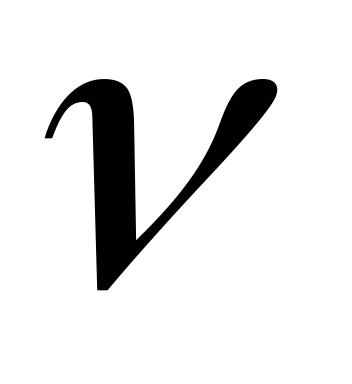 .
. -
Встановіть залежність, що існує між функціями Бесселя індексу
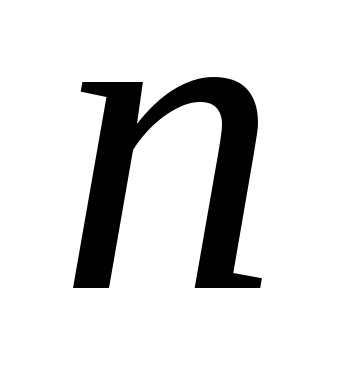 та
та
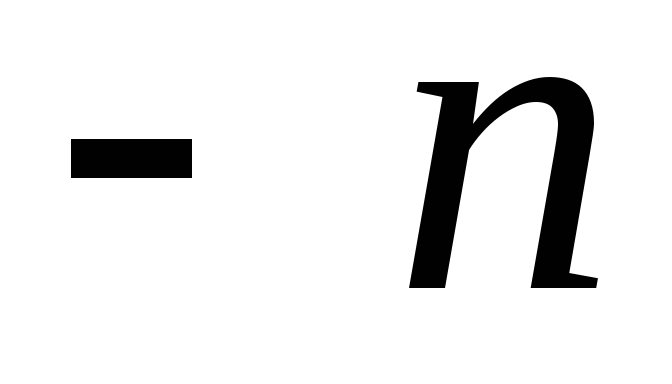 .
. -
Отримайте рекурентні формули для функцій Бесселя.
-
Отримайте інтегральне представлення для функцій Бесселя.
-
Наведіть приклади застосування інтегрального представлення Пуассона.
-
Які з циліндричних функцій можна виразити через елементарні?
-
Які спеціальні функції називаються сферичними?
-
Напишіть рівняння, розв’язками якого є поліноми Лежандра.
-
Напишіть рівняння, розв’язками якого є сферичні функції Лежандра.
-
Як пов’язані між собою будь-які два розв’язки рівняння Лежандра? Напишіть формулу.
-
Як визначається функція Лежандра другого роду? Запишіть формулу.
-
Яка функція є виробничою функцією для системи поліномів Лежандра?
-
Наведіть приклади застосування виробничої функції для поліномів Лежандра.
-
Отримайте рекурентні формули для поліномів Лежандра.
-
Дайте розв’язок задачі про обтікання кулі потоком ідеальної рідини.
Завдання для самостійної роботи
-
Обчислити інтеграли
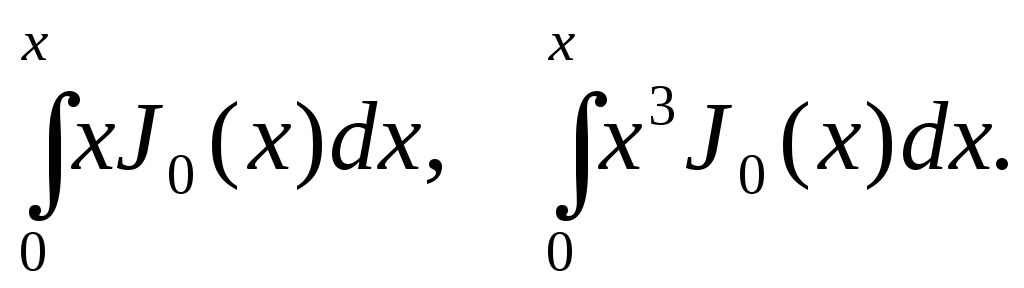
-
Обчислити (виразити через елементарні функції)
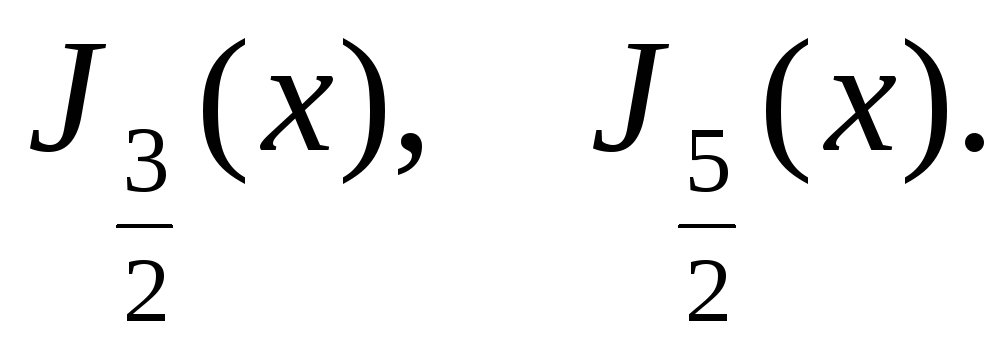
-
Обчислити за формулою (6.31)
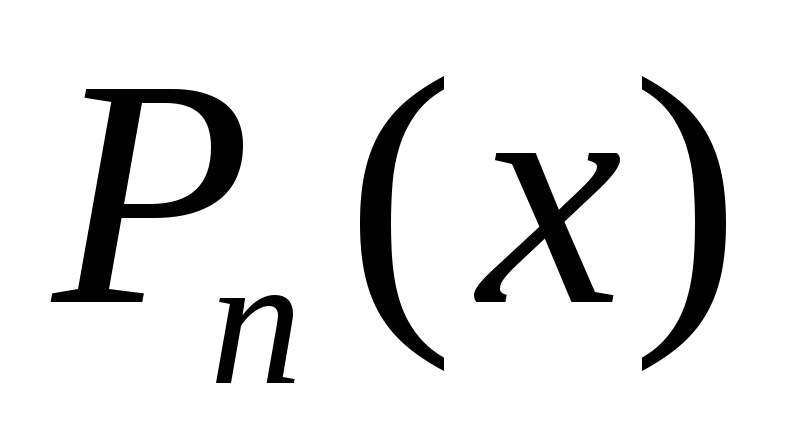 при
при
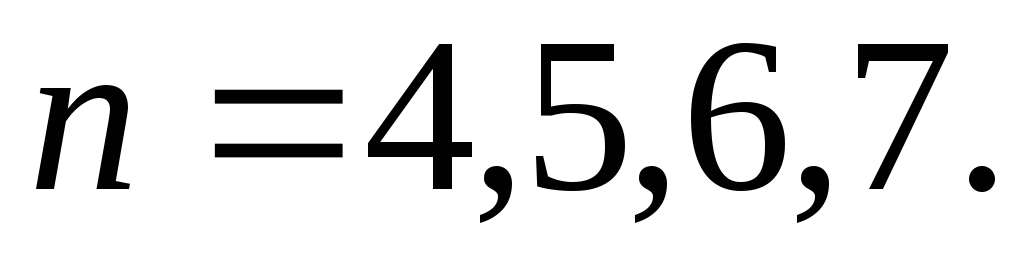
-
Записати загальний розв’язок рівняння
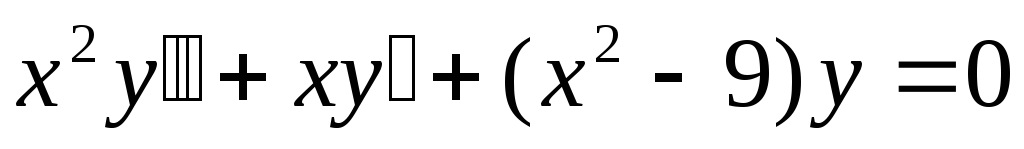 .
.
-
Записати загальний розв’язок рівняння
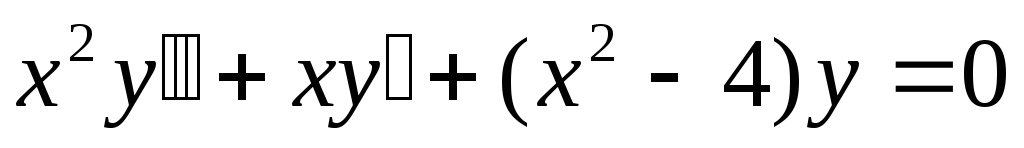 .
.
-
Записати загальний розв’язок рівняння
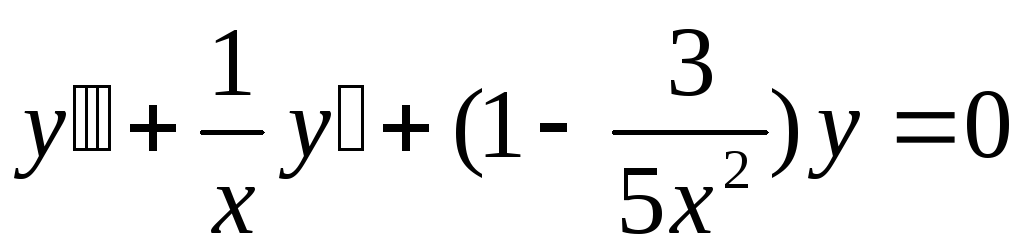 .
.
-
Написати рівняння, розв’язком якого були б функції

-
Написати інтегральне представлення Пуассона функції
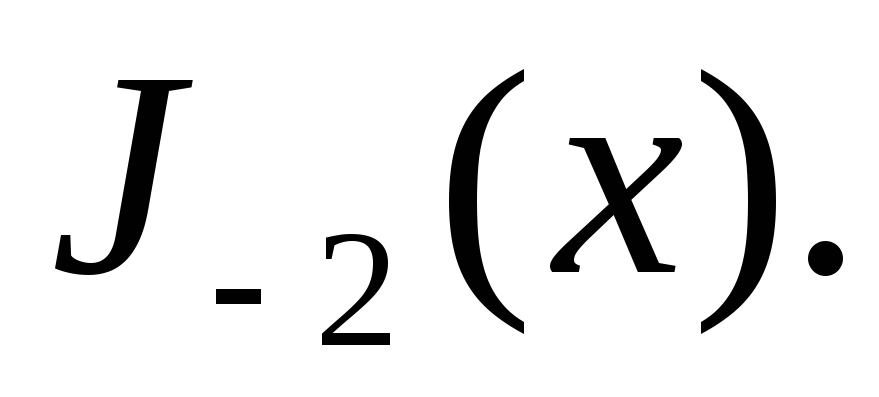
-
Знайти температуру нескінченного циліндра радіуса
 за умови, що на його поверхні підтримується
температура, рівна нулю, а початкова
температура дорівнює
за умови, що на його поверхні підтримується
температура, рівна нулю, а початкова
температура дорівнює
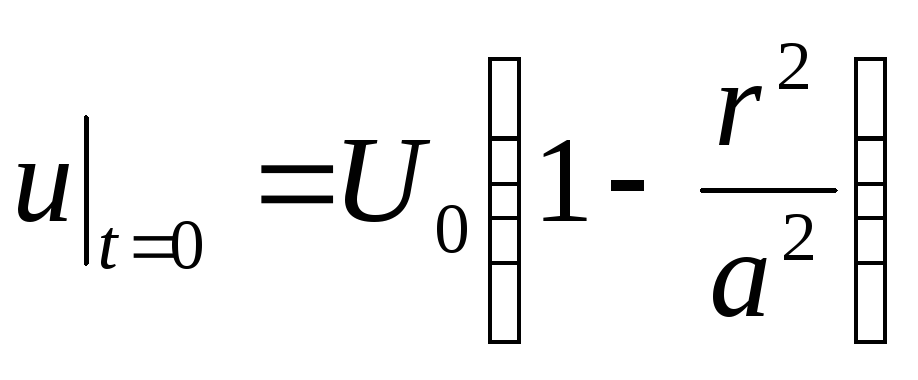 .
.
-
Вивчити віссесиметричні коливання круглої мембрани радіуса
 ,
викликані ударним імпульсом
,
викликані ударним імпульсом
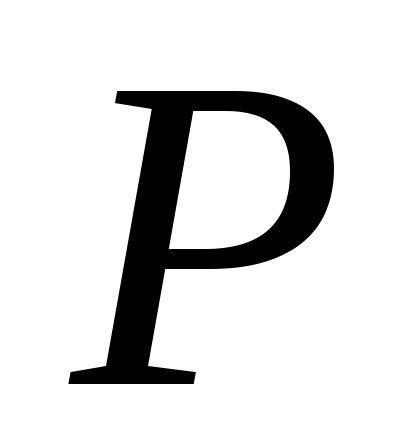 ,
прикладеним у момент
,
прикладеним у момент
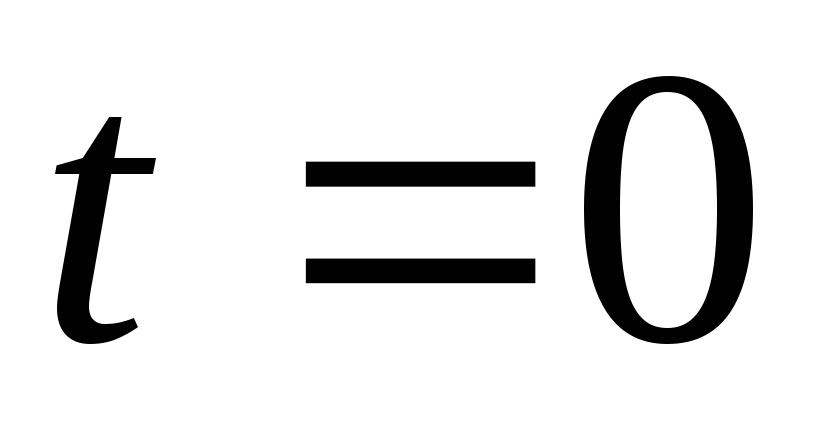 та розподіленим по площі круга радіуса
та розподіленим по площі круга радіуса
 ,
,
 – поверхнева густина мембрани, а
початкові умови такі:
– поверхнева густина мембрани, а
початкові умови такі:
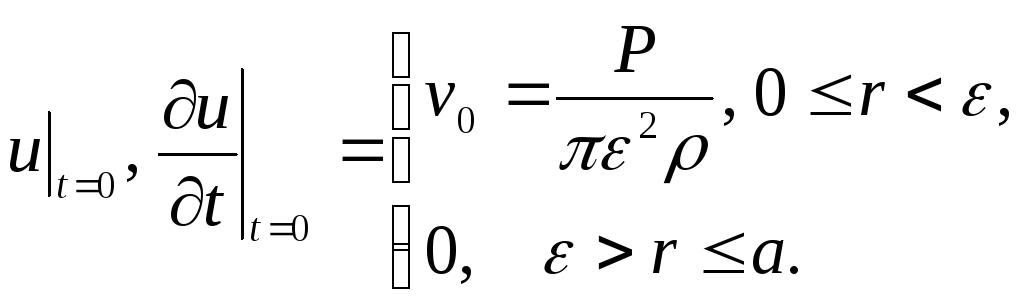 .
.
-
Навести загальний розв’язок задачі про коливання кільцевої мембрани, закріпленої на колах
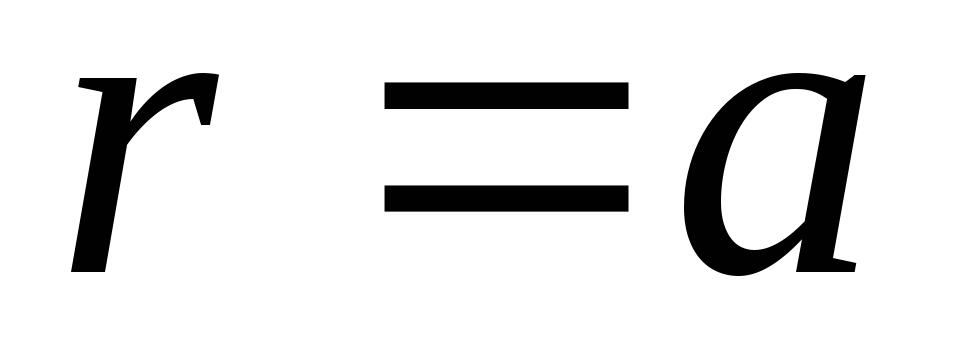 та
та
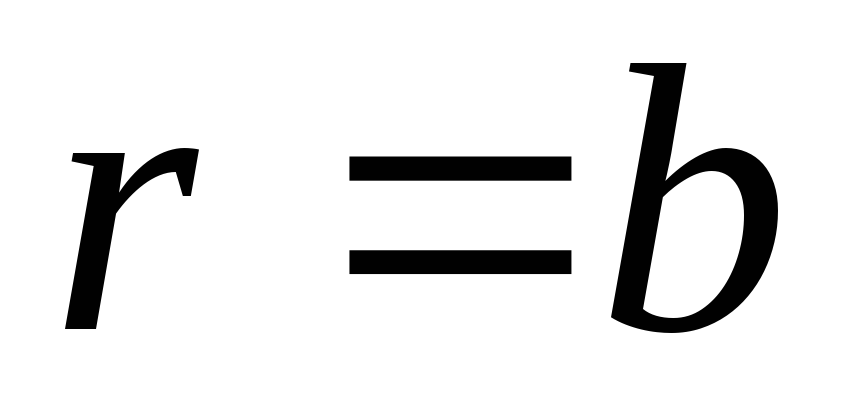 при довільних початкових умовах
при довільних початкових умовах
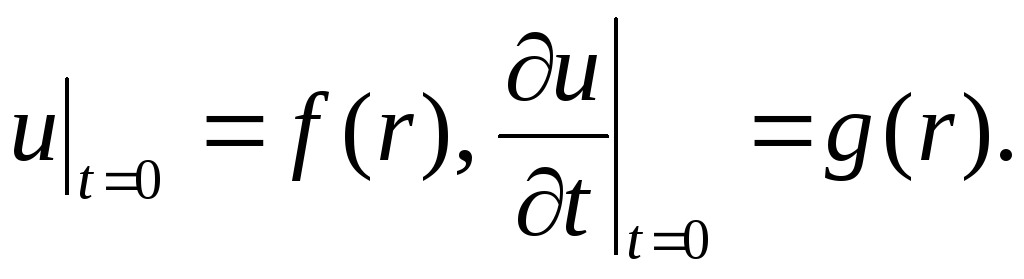
-
Дослідити вільні пружні поперечні коливання круглої плити радіуса
 із жорстко закріпленим краєм при
довільних початкових умовах
із жорстко закріпленим краєм при
довільних початкових умовах
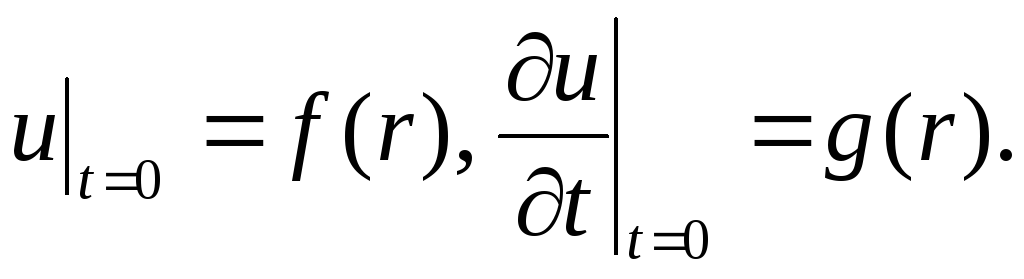
-
На круглу мембрану, закріплену по краю, діє зовнішня гармонічна сила
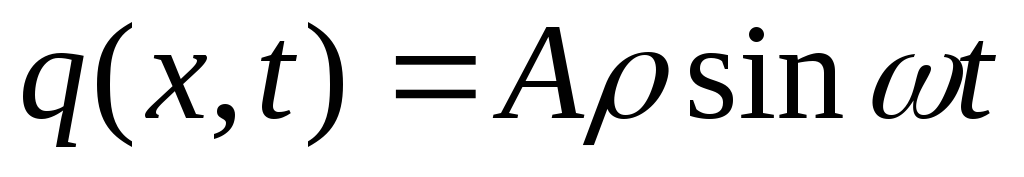 ,
неперервно розподілена по усій площі
мембрани. Перевірте, що вимушені
коливання мембрани такі
,
неперервно розподілена по усій площі
мембрани. Перевірте, що вимушені
коливання мембрани такі
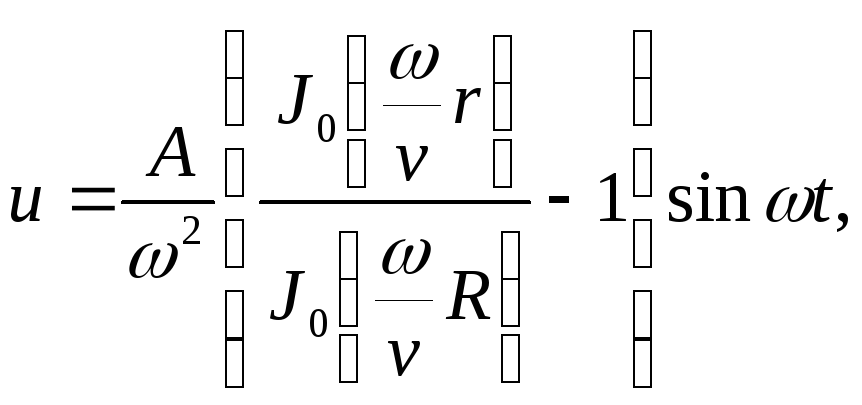 де
де
 –
радіус мембрани.
–
радіус мембрани.
-
Обчислити інтеграли
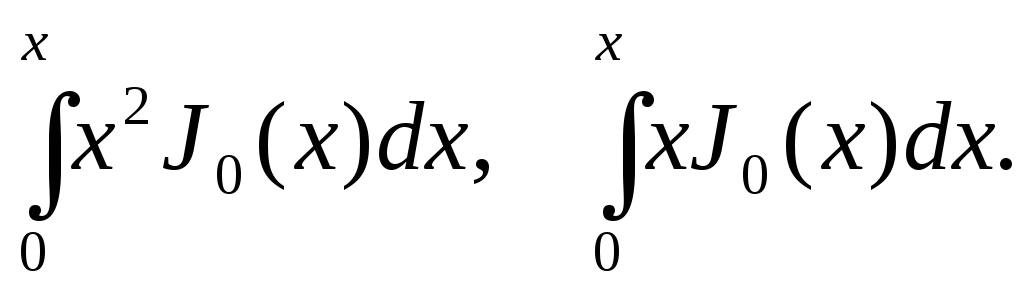
-
Знайти температуру нескінченного циліндра радіуса
 за умови, що на його поверхні підтримується
температура, рівна нулю, а початкова
температура дорівнює
за умови, що на його поверхні підтримується
температура, рівна нулю, а початкова
температура дорівнює
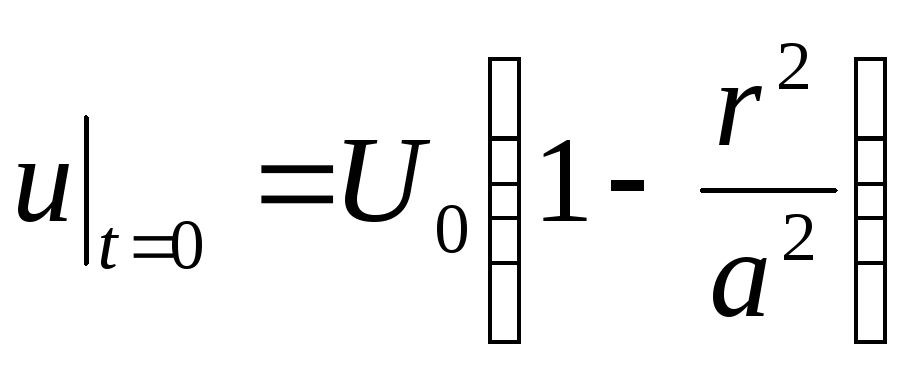 .
.
-
Знайти закон вирівнювання вісьосиметричного початкового розподілу температури
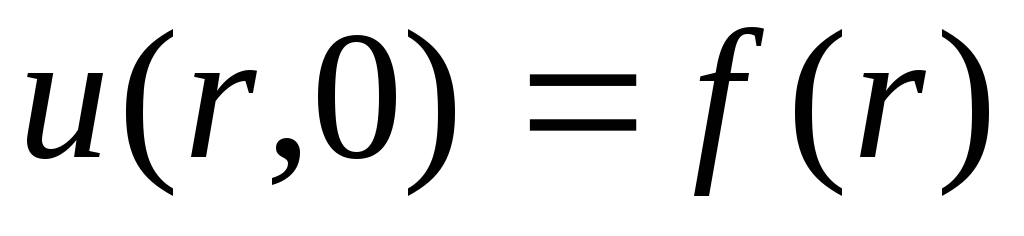 у нескінченному циліндрі радіуса
у нескінченному циліндрі радіуса
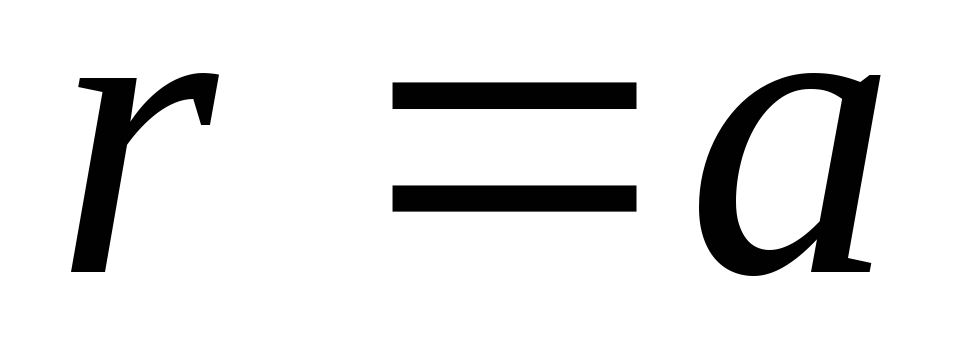 ,
бічна поверхня якого теплонепроникна.
,
бічна поверхня якого теплонепроникна.
-
Написати рівняння, розв’язком якого були б функції
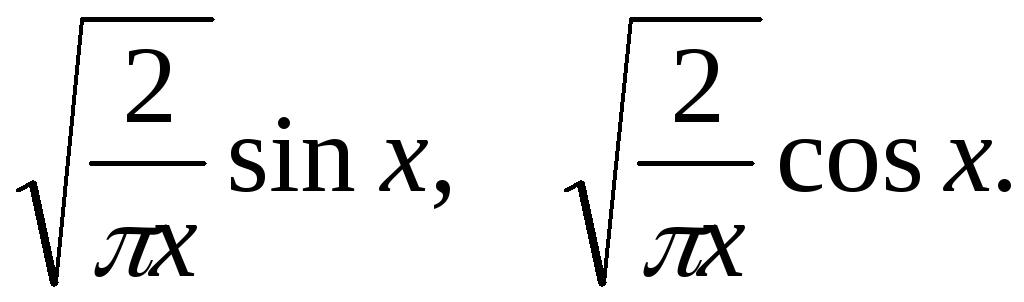
-
Циліндр радіуса
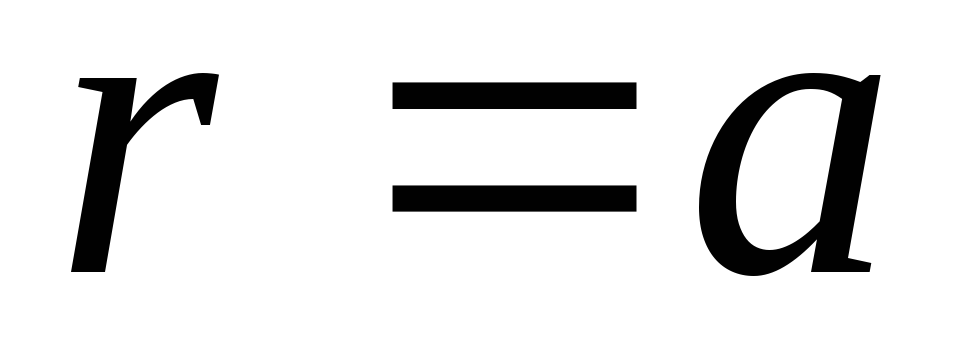 нагрівають до температури
нагрівають до температури
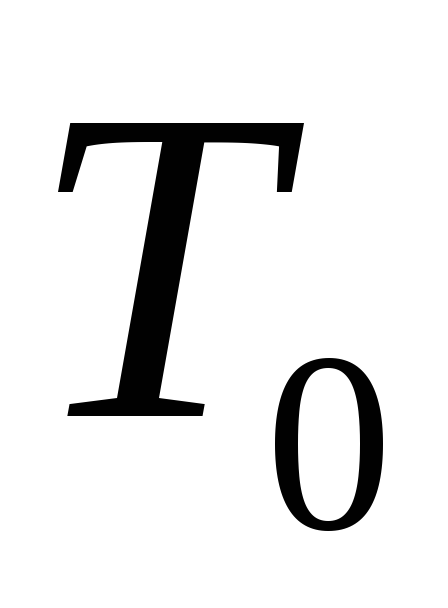 ,
а потім охолоджують з поверхні таким
чином, що її температура поверхні,
починаючи з моменту часу
,
а потім охолоджують з поверхні таким
чином, що її температура поверхні,
починаючи з моменту часу
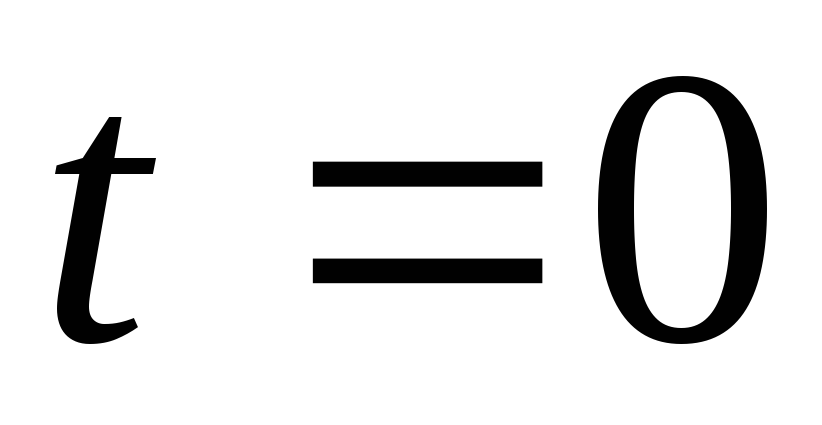 ,
підтримується сталою та рівною нулю.
Знайти закон охолодження циліндра,
вважаючи, що розподіл температури в
усіх поперечних перерізах однаковий.
,
підтримується сталою та рівною нулю.
Знайти закон охолодження циліндра,
вважаючи, що розподіл температури в
усіх поперечних перерізах однаковий.
-
Знайти температуру круглого нескінченного циліндра радіуса
 за умови, що на його поверхні відбувається
конвективний теплообмін із середовищем,
температура якого дорівнює нулю, а
початкова температура дорівнює
за умови, що на його поверхні відбувається
конвективний теплообмін із середовищем,
температура якого дорівнює нулю, а
початкова температура дорівнює
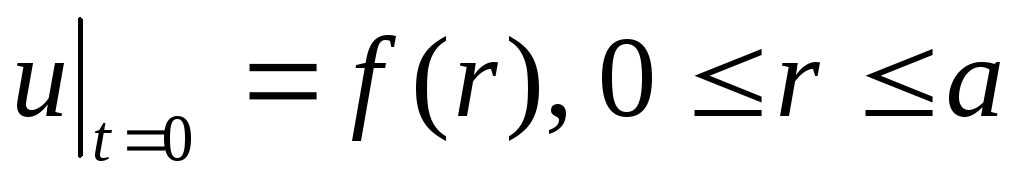 .
Розглянути окремий випадок, коли
.
Розглянути окремий випадок, коли
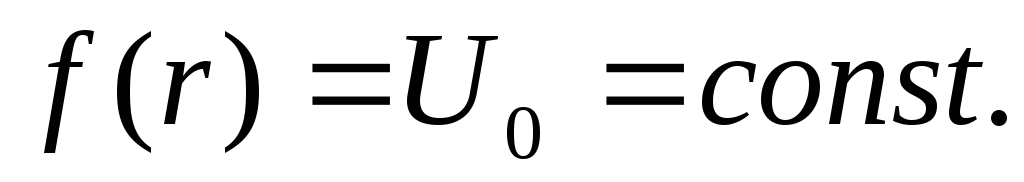
-
В циліндрі радіуса
 та висотою
та висотою
 протягом експерименту температура
нижньої основи та бічної поверхні
дорівнює нулю, а температура верхньої
основи є функцією від
протягом експерименту температура
нижньої основи та бічної поверхні
дорівнює нулю, а температура верхньої
основи є функцією від
 .
Вказівка:
для розв’язання задачі потрібно знайти
такий інтеграл рівняння Лапласа, який
би задовольняв умови
.
Вказівка:
для розв’язання задачі потрібно знайти
такий інтеграл рівняння Лапласа, який
би задовольняв умови
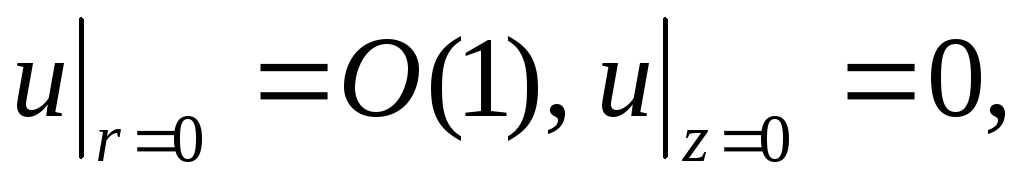
 .
.
-
Вивчити вісьосиметричні коливання круглої мембрани радіуса
 ,
викликані ударним імпульсом
,
викликані ударним імпульсом
 ,
прикладеним у момент
,
прикладеним у момент
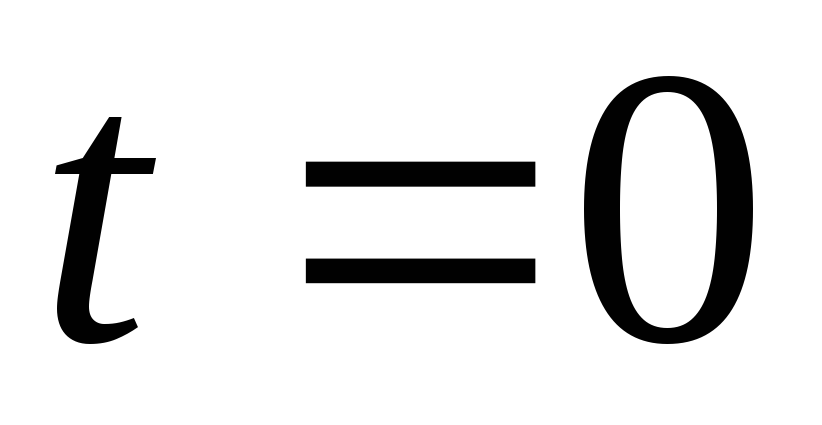 та розподіленим по площі круга радіуса
та розподіленим по площі круга радіуса
 ,
,
 – поверхнева густина мембрани, а
початкові умови такі:
– поверхнева густина мембрани, а
початкові умови такі:
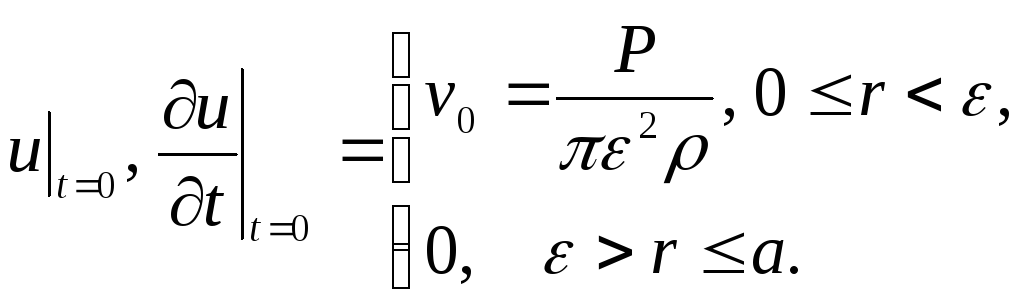 .
.
-
Розв’язати задачу 19 з припущенням, що бічна поверхня циліндра покрита теплонепроникним чохлом. Вказівка: третю крайову умову в задачі 19 замінити на
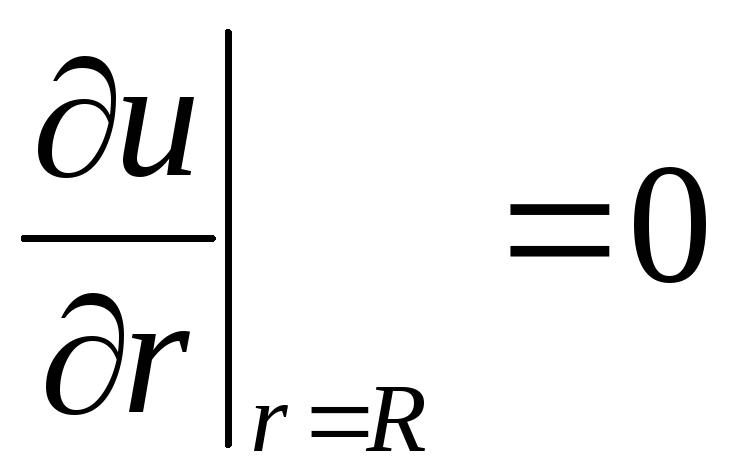 .
.
-
Розв’язати задачу 19 з припущенням, що бічна поверхня циліндра вільно охолоджується у повітря, яке має нульову температуру. Вказівка: третю крайову умову в задачі 19 замінити на
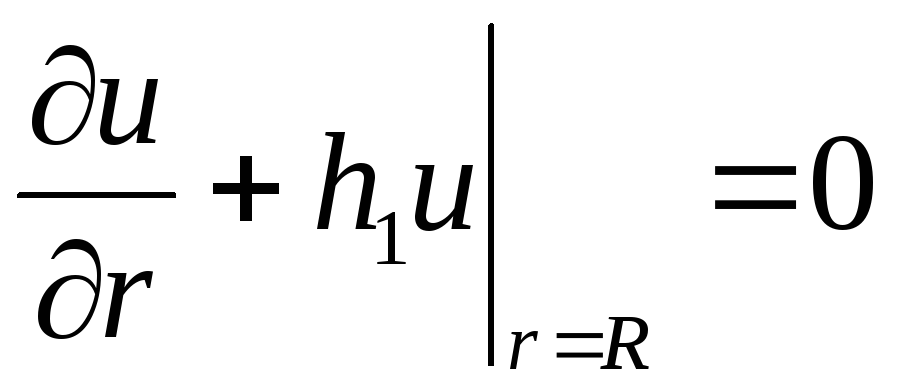 .
.
-
Центр круглої мембрани відхилений при
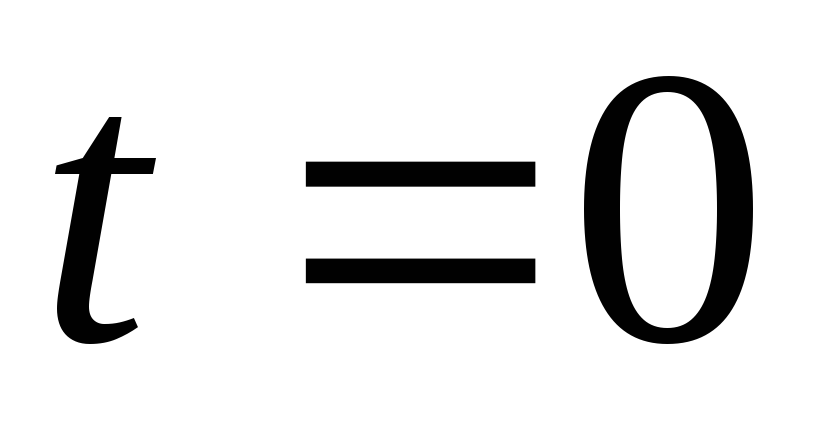 на малу висоту
на малу висоту
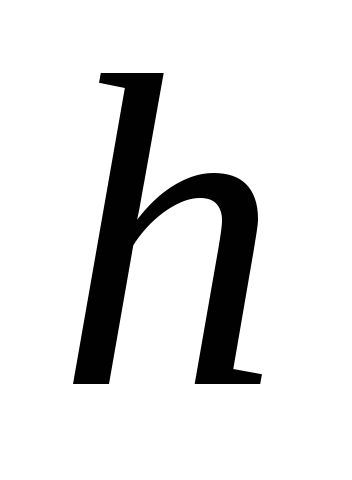 .
Початкові швидкості точок мембрани
рівні нулю. Дослідити коливання мембрани.
Вказівка:
початкові
умови такі:
.
Початкові швидкості точок мембрани
рівні нулю. Дослідити коливання мембрани.
Вказівка:
початкові
умови такі:
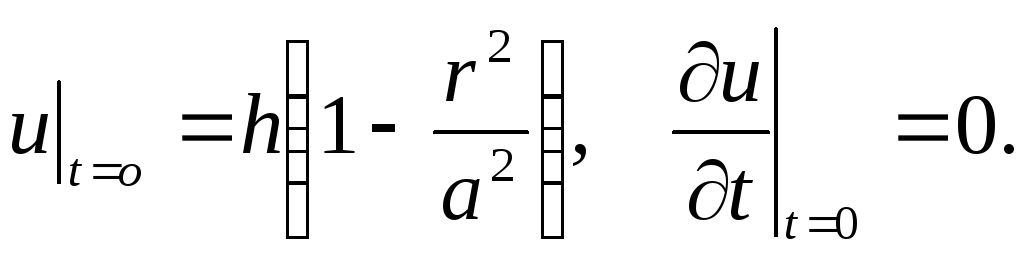
-
Навести загальний розв’язок задачі про коливання кільцевої мембрани, закріпленої на колах
 та
та
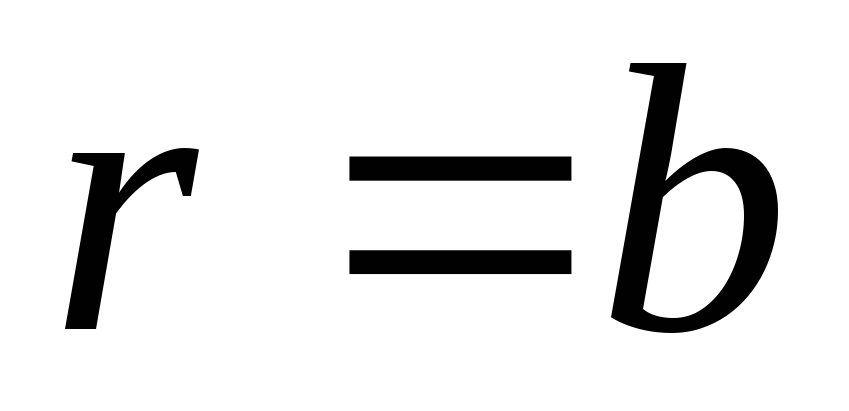 при довільних початкових умовах
при довільних початкових умовах
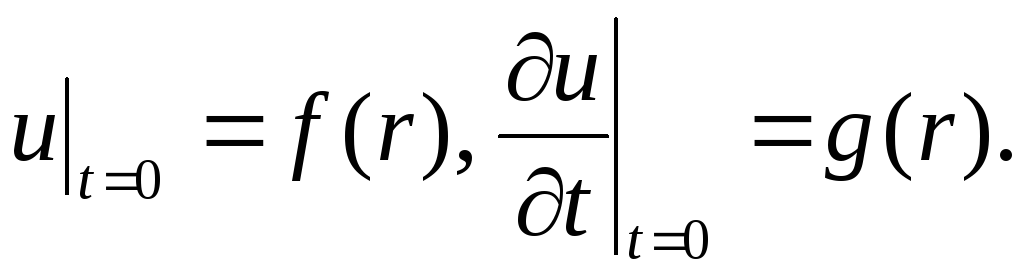
-
Циліндр, радіус якого
 і висота
і висота
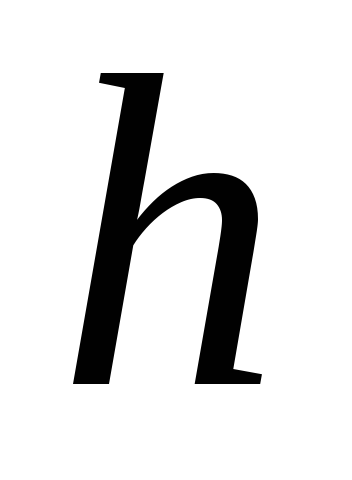 ,
має температуру обох основ, рівну нулю,
а температура бічної поверхні є функцією
від
,
має температуру обох основ, рівну нулю,
а температура бічної поверхні є функцією
від
 .
Знайти стаціонарну температуру
внутрішніх точок.
.
Знайти стаціонарну температуру
внутрішніх точок.
-
Розкласти функцію
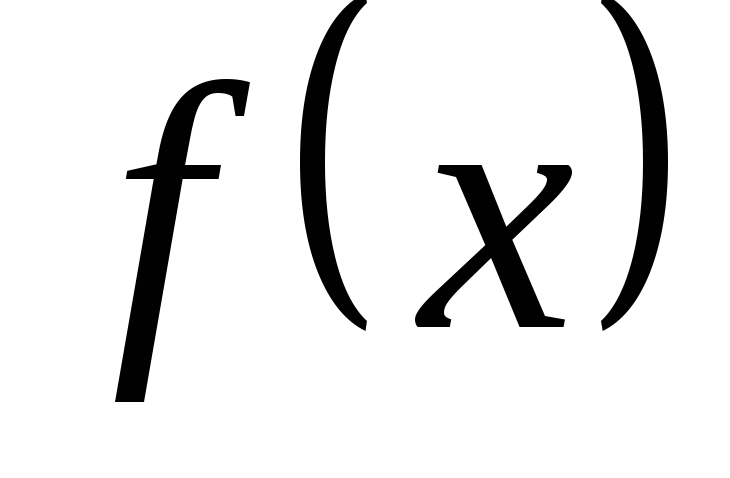 на інтервалі
на інтервалі
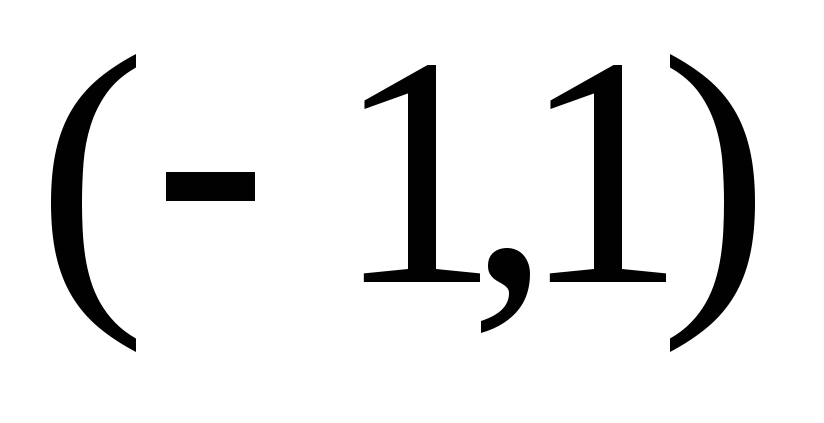 ,
якщо
,
якщо
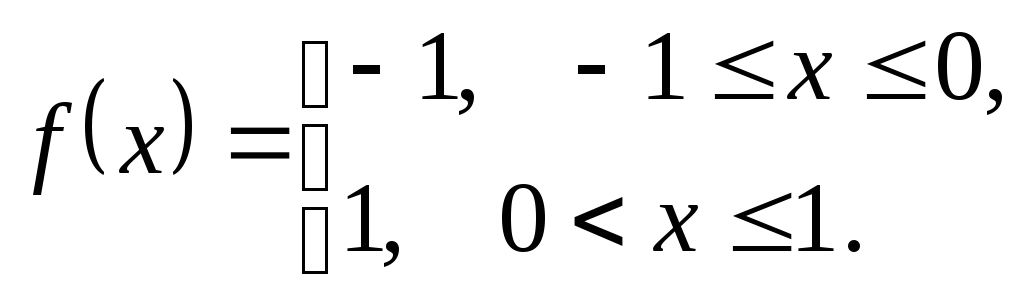
-
Розв’язати рівняння коливання круглої мембрани
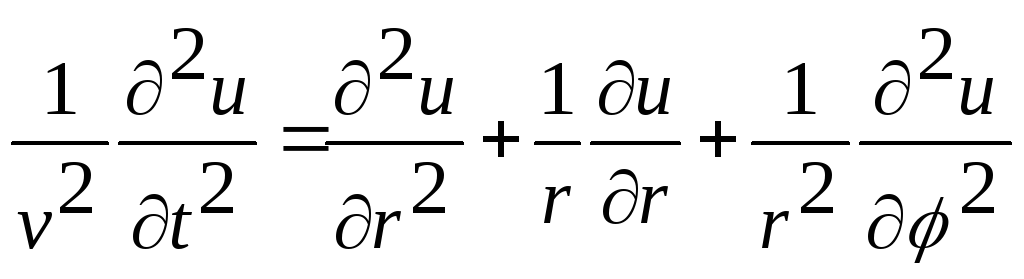 при крайовій умові (мембрана закріплена
по контуру)
при крайовій умові (мембрана закріплена
по контуру)
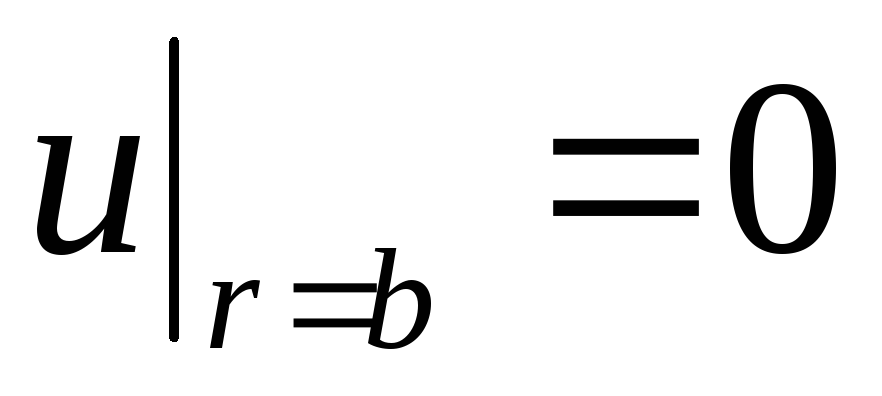 та початкових умовах
та початкових умовах
 ,
початкових умовах
,
початкових умовах
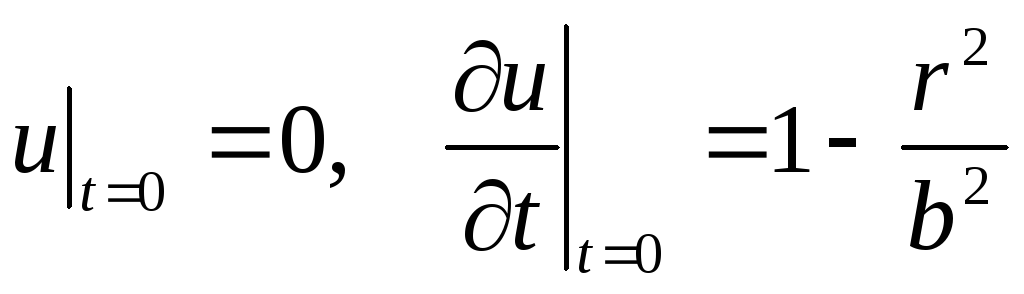 .
.
-
Написати інтегральне представлення Пуассона функції
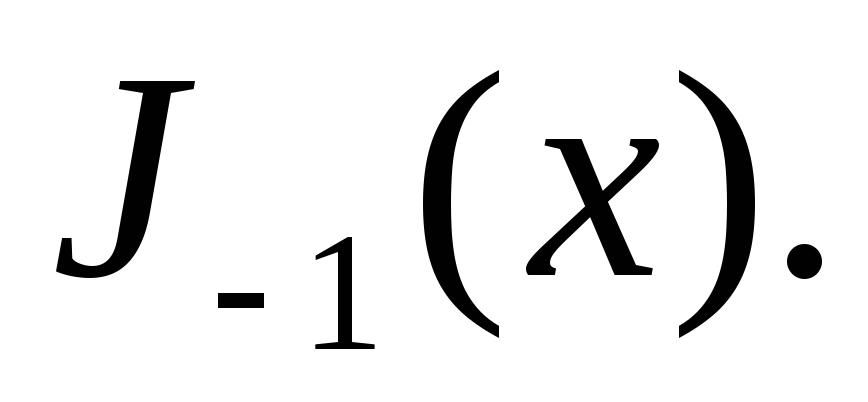
-
Дослідити пружні поперечні коливання круглої плити радіуса
 із закріпленим краєм при довільних
початкових умовах
із закріпленим краєм при довільних
початкових умовах
 .
.
