2. Метод вращения

Идея этого метода также состоит в получении на необходимых местах у матрицы системы нулей, но с помощью операторов поворота в плоскостях Ох₁х₂, Ох₁х₃, Ох₂х₃. Соответствующие матрицы поворотов легко получаются из матрицы (18):

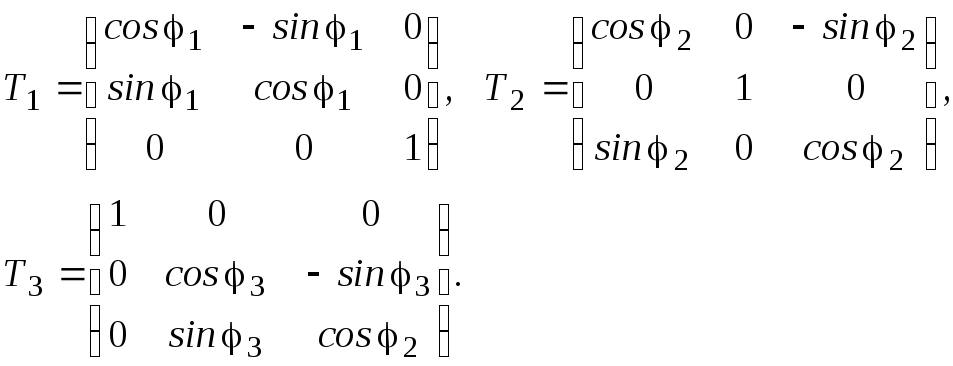
Вместо (31) за три шага получим систему

(Т₃Т₂Т₁ А)Х= Т₃Т₂Т₁ В, (33)

матрица которой имеет ступенчатый вид.

Покажем, как определить в общем случае для n=3 угол поворота (точнее требуемые значения cos₁ и sin₁), позволяющий получить нуль на месте (2,1) у матрицы системы. Пусть

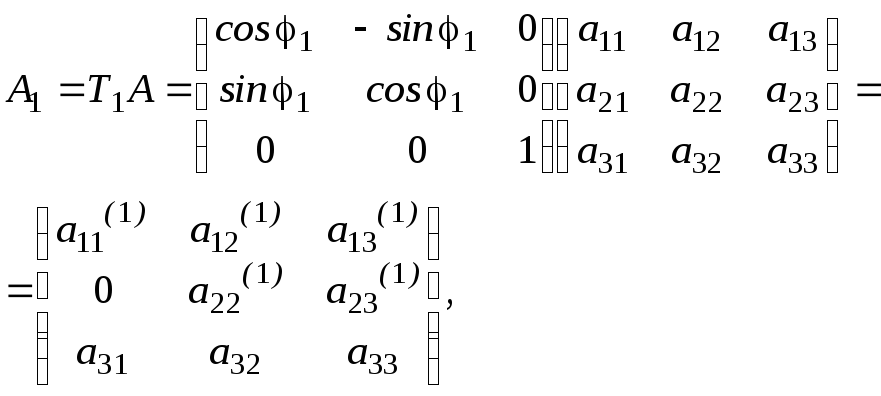
где а₂₁0 (если а₂₁=0, то поворот в плоскости Ох₁х₂ не нужен), мы учли, что третья строка в новой матрице А₁ совпадает с третьей строкой исходной матрицы А.

Имеем 0=а₂₁⁽¹⁾=sin₁a₁₁+cos₁a₂₁, те. . Можно выбрать угол ₁ так, что

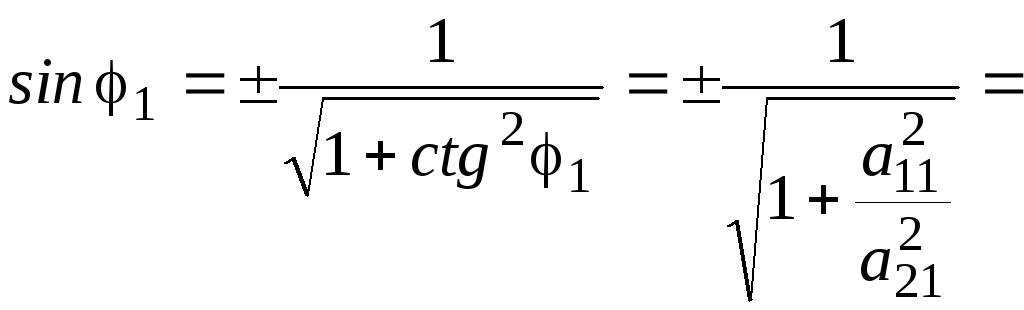
=, т.е. выбрать знак sin₁ такой же, как у числа a₂₁. Тогда cos₁= (cos₁=ctg₁ sin₁).

Итак,

sin₁=, cos₁=. (34)

Формулы (34) дают возможность провести первый шаг метода вращения. Другие шаги проделываются аналогично: А₂=Т₂А₁, А₃=Т₃А₂= Т₃Т₂ Т₁ А – матрица заключительной системы (33).

Тема 6. Метод гаусса (полная версия)

Здесь мы опишем алгоритм Гаусса для произвольных СЛАУ: в примере 1 была рассмотрена его простейшая версия.

Первый шаг состоит в получении у матрицы А:В первого столбца в виде 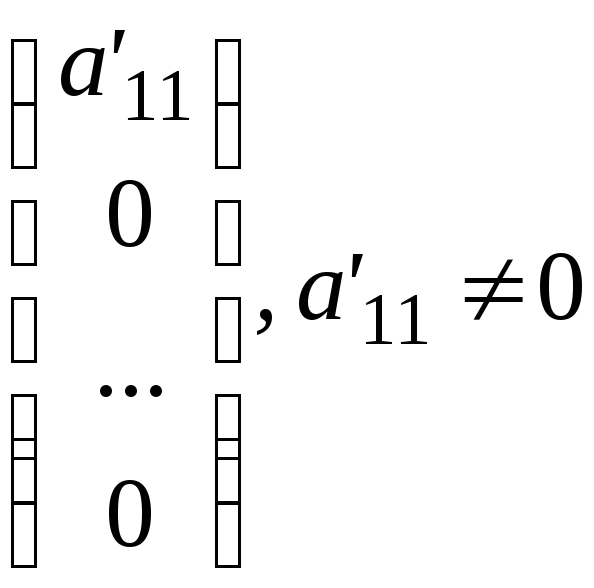. В случае а₁₁0 этого легко добиться с помощью преобразований G 3). Если же а₁₁=0, то можно поменять строки так, чтобы новый .

Второй шаг (аналогично, общий шаг) отличается от первого шага тем, что возможна ситуация, когда с помощью преобразований строк не удается добиться, чтобы . В этой ситуации второй столбец можно поменять местами с одним из следующих, чтобы добиться искомого требования . Единственный случай, когда этого невозможно добиться, когда на каком-то шаге мы получаем матрицу вида

.

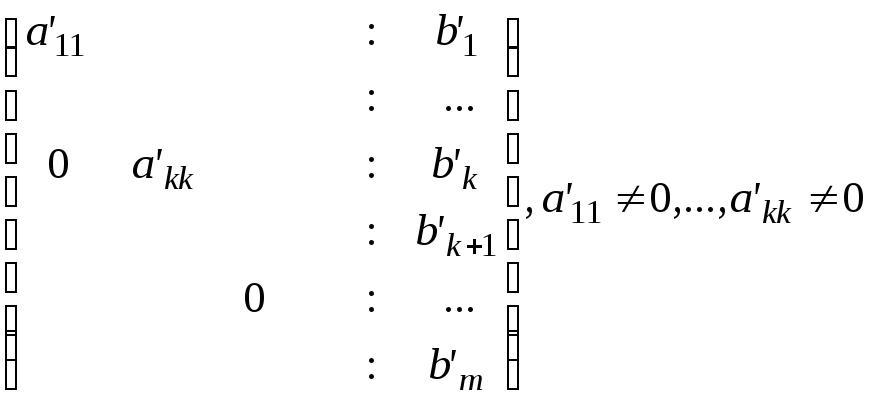Возможны два варианта.

I вариант.

Все b'_k+1,…,b'_m равны нулю. Отбрасываем «нулевые» уравнения Получаем требуемую ступенчатую матрицу.

II вариант.

Найдется хотя бы одно из чисел b'_k+1,…,b'_n, отличное от нуля. В этом случае СЛАУ решений не имеет.

Таким образом в случае, когда СЛАУ имеет решения, ее расширенную матрицу А:В можно привести к ступенчатому виду:

.

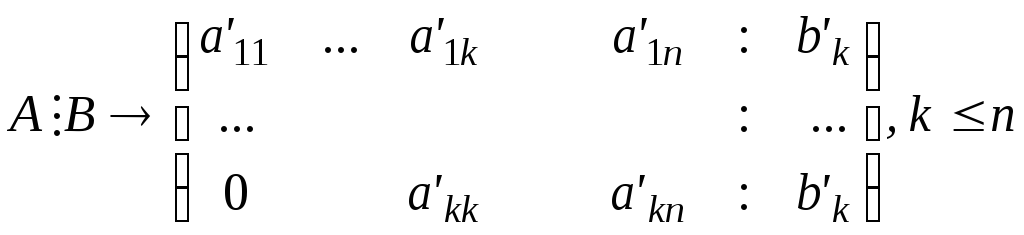Тогда решение СЛАУ (3)

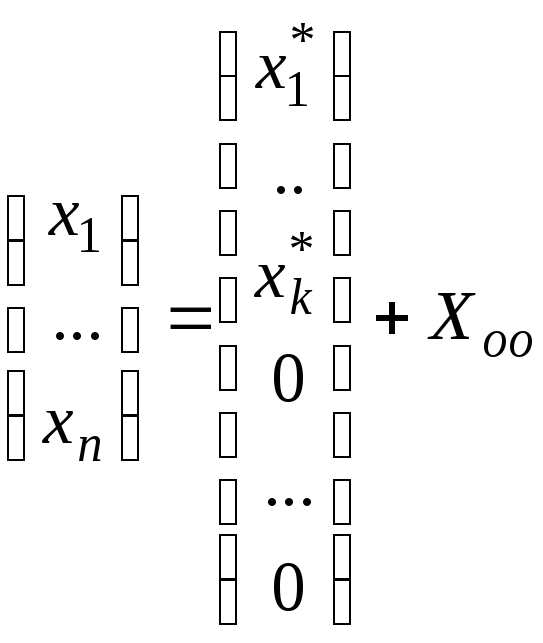, (35)

где определение и способ вычисления Х_оо показаны в примере 5, значения находятся как в примере1 из решения системы, имеющей расширенную матрицу

.

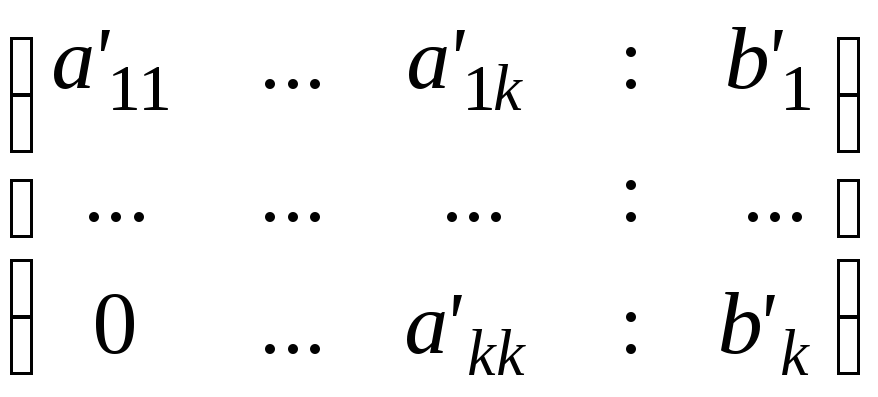Пример11. Решить СЛАУ методом Гаусса

.

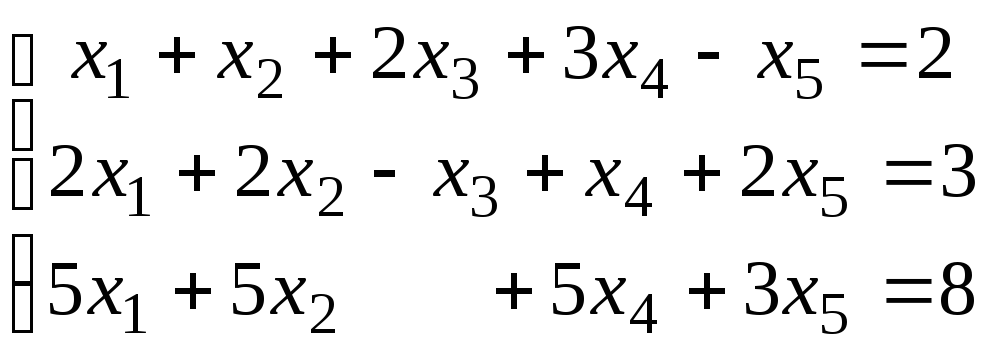Решение. Приведем сначала расширенную матрицу системы к ступенчатому виду

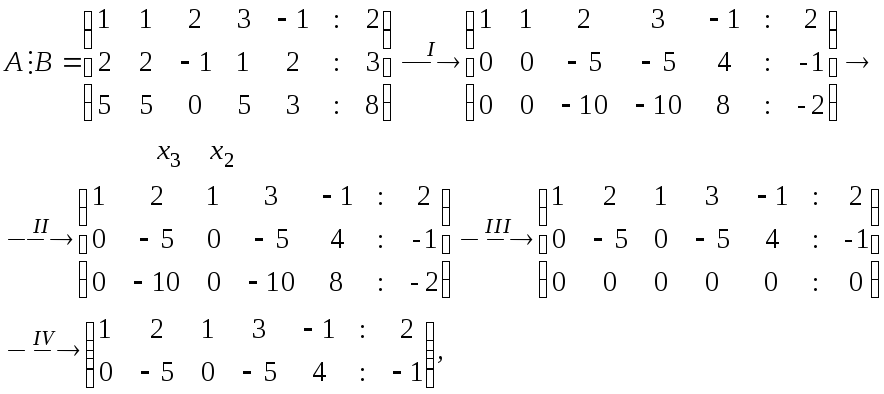и шаг I состоит в применении двух преобразований G 3): ; шаг II состоит в перестановке второго и третьего столбцов, при этом мы должны запомнить, что с этого момента второй столбец-столбец коэффициентов при переменной х₃ (а третий столбец – при х₂); шаг III состоит в применении преобразования G 3): , наконец, шаг IV – отбрасывание нулевой строки.

Переменные х₁, х₃ – основные, х₂, х₄, х₅  дополнительные.

1. Пусть все дополнительные переменные равны нулю, т.е. х₂=х₄=х₅=0. Для нахождения х₁ и х₃ решим систему

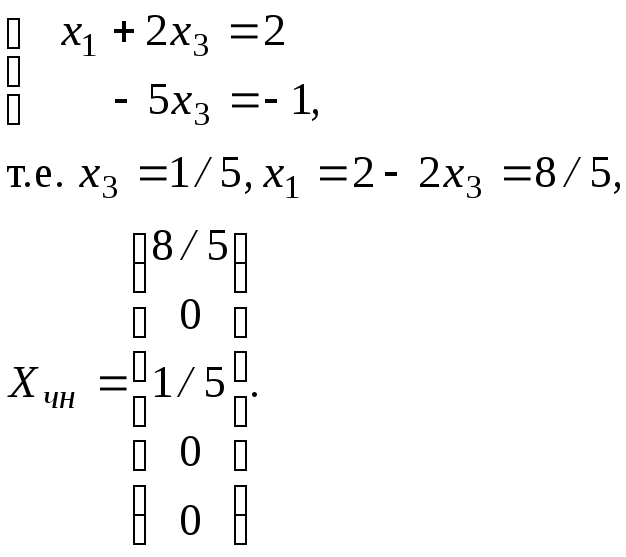
2. Теперь найдем Х_оо, решая однородную систему

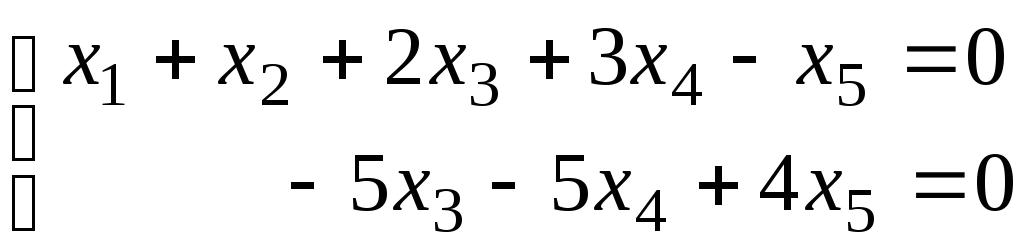(36)

аналогично примеру 5.

Найдем базисные решения

Пусть х₂ =1, х₄=0, х₅=0. Система (36) примет вид

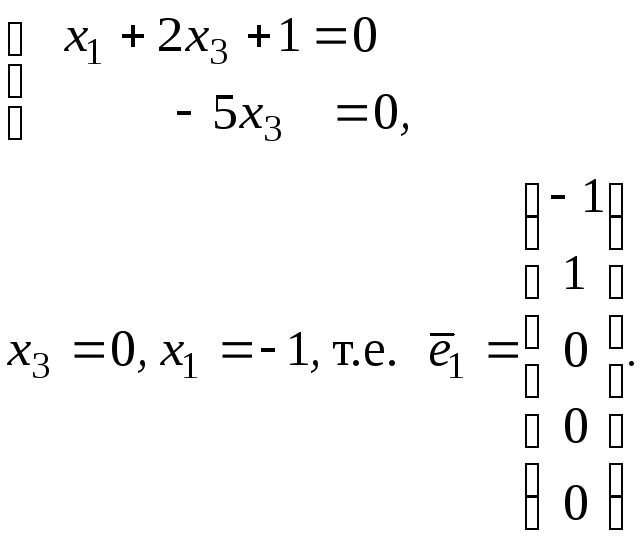
Найдем при х₂=0, х₄=1, х₅=0:

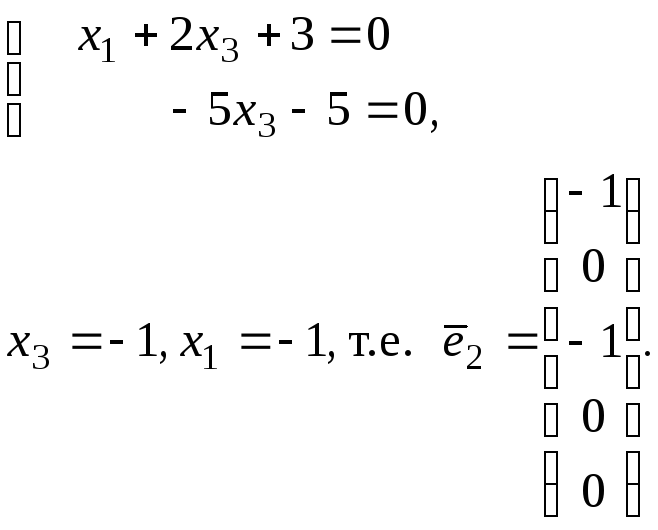
Наконец, найдем при х₂=0, х₄=0, х₅=1:

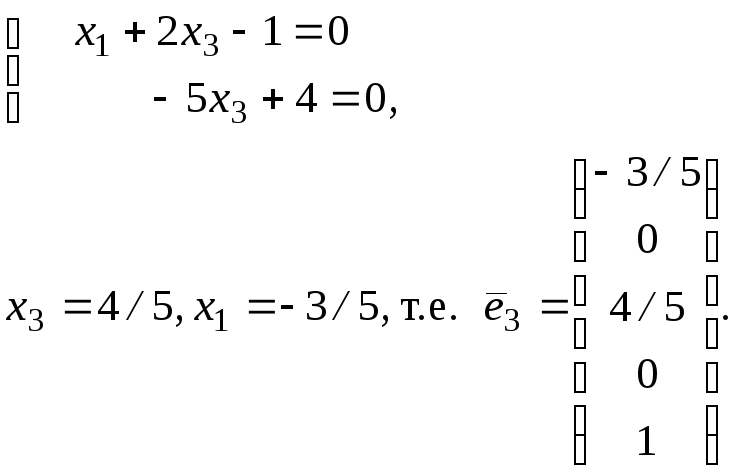
3. По формуле (35) окончательно

,

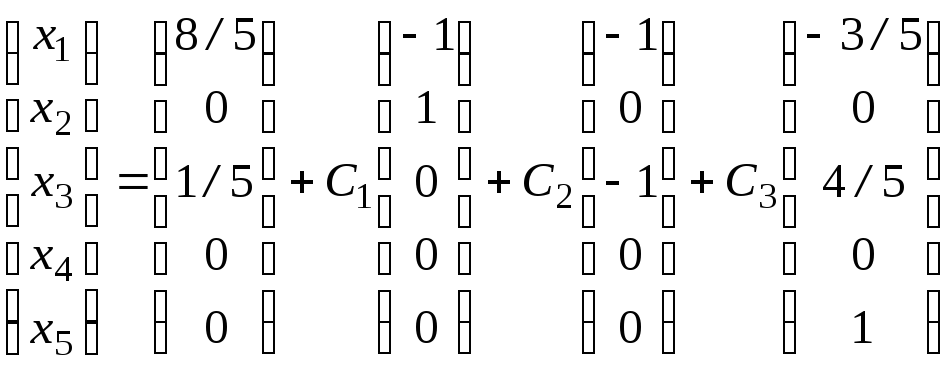где С₁, С₂, С₃ – любые вещественные числа.

Приведем в заключение примерную тематику контрольной работы, варианты расчетно-графической работы и вопросы к зачету.