3. Квадратичные функционалы

Определение 10. Квадратичным функционалом q(a), где q : LR, порожденным симметричным билинейным функционалом (a, b), называется функционал, определяемый формулой

q(a)= (a, b), (28)

а матрицей квадратичного функционала в базисе  называется матрица ()_ где (a, b) – порождающий q симметричный билинейный функционал.

Пример 7. Пусть L=Vect₂, , (a, b) – билинейный функционал, - квадратичный функционал, порожденный (a, b). Выразить через х и у – координаты вектора .

Решение. По формулам (24) и (28)

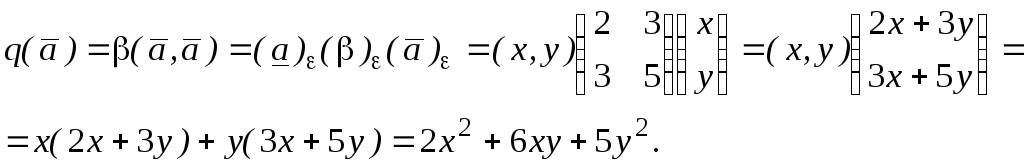
Итак, = - квадратичная форма от координат х, у вектора .

Пример 8. Пусть L=Vect₂, ,

. Найти матрицу (q)_.

Решение. Очевидно, что данная задача обратна задаче, решенной в примере 7, поэтому .

Пример 9. Пусть L=Vect₂, ,

. Найти ортонормированный базис пространства L такой, что матрица (q)_F – диагональна.

Решение. Найдем сначала, как в примере 8, матрицу (q)_.:

.

Рассмотрим в пространстве L линейный оператор Т, матрица которого в базисе  совпадает с этой матрицей, т.е.

.

Найдем собственные значения и собственные векторы этой матрицы. Запишем и решим характеристическое уравнение (21):

,

или (2-)(5-)-4=0, ²-7+6=0, откуда найдем собственные значения ₁=1, ₂=6.

Теперь найдем собственные векторы. Если ₁=1, то

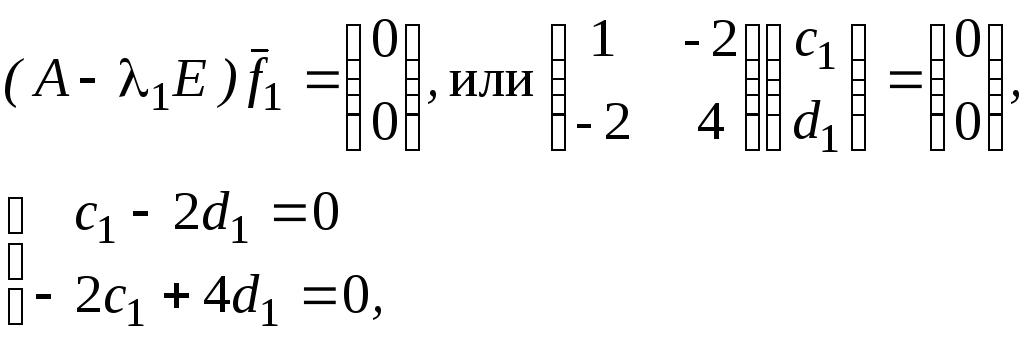
Откуда d₁=kR, c₁=2d₁=2k, . Выберем значение k так, чтобы , то можно взять , т.е.

. (29)

Аналогично для ₂=6 получим :

.

Пусть с₂=kR, тогда d₂ =-2c₂=-2k, .

Имея в виду геометрические приложения (см. ниже задачу 3 контрольной работы), из двух значений , обеспечивающих требование ||=1, выберем , т.е.

. (30)

Векторы (29) и (30) образуют искомый ортонормированный базис , т.к.

Это условие обеспечивает ортогональность матрицы С перехода от базиса  к базису F:

, С^-1=С^Т

(см. равенства (10) и (27)). Но тогда (см. (25) и (26)):

(q)_F=()_F=(T)_F=,

где - порождающий q симметричный билинейный функционал.

Задача, поставленная в примере 9, полностью решена.

Эта задача играет важную роль в геометрии при построении кривых и поверхностей второго порядка.

Тема 5. Методы отражения и вращения решения слау

Мы рассмотрим на простых примерах два новых метода решения СЛАУ. В основе их наряду с идеей метода Гаусса получения необходимого количества нулей у матрицы системы, важную роль играют геометрические операторы отражения и вращения. Проиллюстрируем эти соображения для системы из примера 1.

1. Метод отражения.

Умножим на матрицу отражения (17) обе части равенства (4). Получим систему

((Т)_А)Х=(Т)_В, (31)

матрицей которой является

.

Выберем нормальный вектор так, чтобы отраженный столбец имел вид . Так как при отражении длина вектора не меняется, то возьмем =|₁| (можно взять =-|₁|, других вариантов нет). Но тогда координаты найдем из формулы

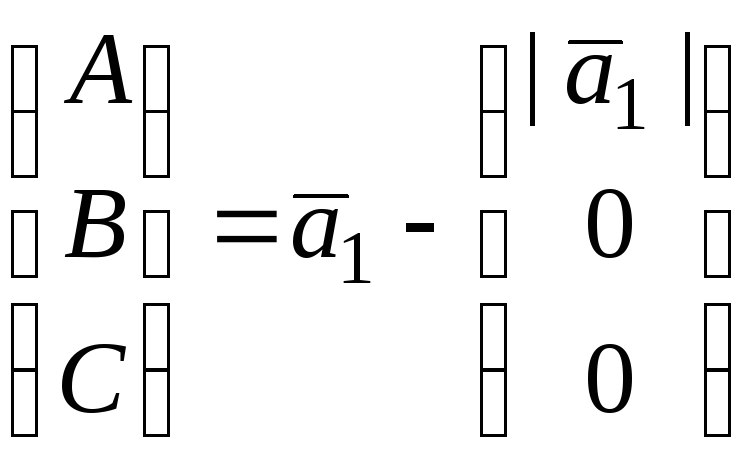. (32)

При этом выборе матрица системы (31) будет иметь первый столбец , что соответствует выполнению двух преобразований вида G 3) метода Гаусса. Далее систему (31) можно решить либо применяя еще одно отражение, либо каким либо другим методом, например, находя переменные х₂, х₃ с помощью правила Крамера.

Метод отражения является более точным, нежели классический метод Гаусса, так как операция деления у него присутствует только при вычислении матрицы отражения (17), а у всех дробей, содержащихся в этой матрице, числители по модулю не превосходят знаменателя.

Пример 10. Найти матрицу отражения для СЛАУ из примера 1.

Решение. Здесь .

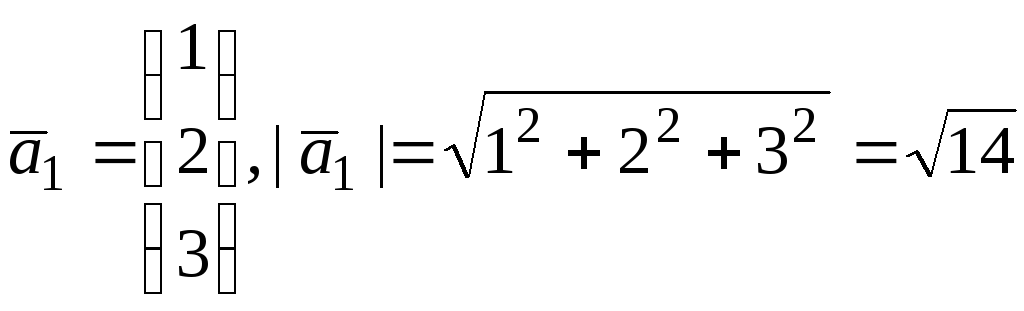По формуле (32) .

Тогда

По формуле (17)

=

.