1. Метод Гаусса (простейшая версия)

Запишем А:В – расширенную матрицу системы (3). Условие |A|0 позволяет привести с помощью преобразований G1)-G3) матрицу (А:В) к ступенчатому виду, причем новая (более простая) матрица соответствует СЛАУ, имеющей то же самое решение Х, что и исходная система.

Пример 1. Решить методом Гаусса систему

Решение. В нашем случае матрица системы

Здесь шаг I состоит из двух преобразований вида G 3):

Целью шага I является получение двух нулей в первом столбце. Шаг II состоит из одного преобразования G 3): на этом шаге мы получаем один нуль во втором столбце, при этом сохраняются нули в первом столбце, полученные на первом шаге.

Запишем СЛАУ, имеющую полученную после шагов I и II расширенную матрицу:

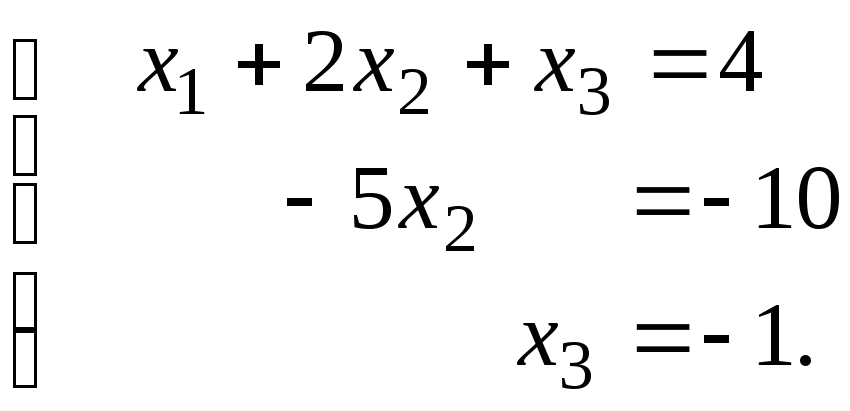
Эту систему решают последовательно «снизу-вверх» (прогонка Гаусса): х₃=-1, х₂=2, х₁=4-2х₂-х₃=4-4-+1=1.

Ответ: х₁=1, х₂=2, х₃=-1.

2. Правило Крамера

Рассмотрим ₁, , _n – определители, полученные из |А| заменой соответственно одного из столбцов на В ( в ₁ заменяем первый столбец на В, в ₂ – второй и т.д.). Тогда значения неизвестных находятся по формулам Крамера:

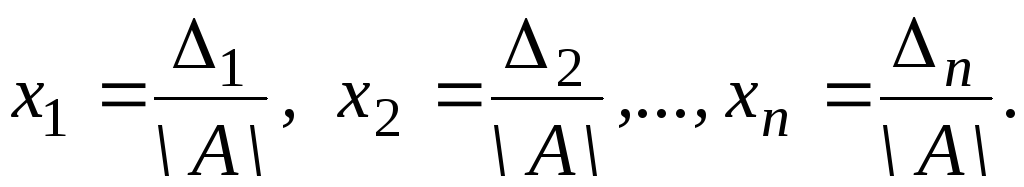(5)

Пример 2. Решить систему из примера 1 с помощью правила Крамера.

Решение. Вычислим определители |A|, ₁, ₂, ₃ по формуле (2):

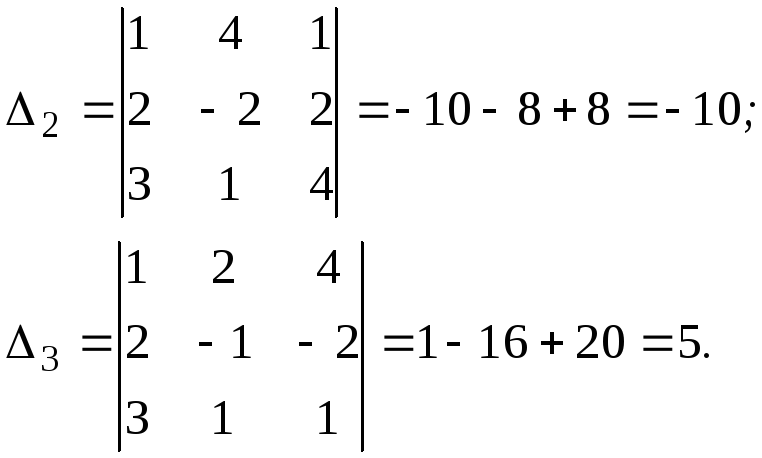
По формулам (5) получим

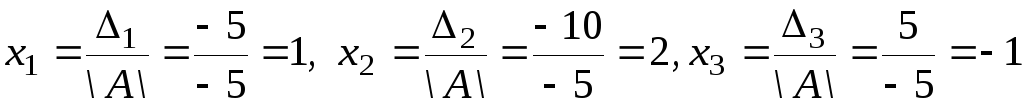, что совпадает с ответом, полученным ранее методом Гаусса.

3. Метод применения обратной матрицы

Определение2. Матрица А^-1 называется обратной для квадратной матрицы А. если

А^-1А=АА^-1=Е.

Если |A|0, то обратная матрица А^-1 существует и единственна. Умножая обе части равенства (4) на А^-1, получим А^-1(АХ)=А^-1В, или, используя свойство ассоциативности умножения матриц,

(А^-1А)Х=А^-1ВЕХ= А^-1В Х=А^-1В. (6)

Формула (6) позволяет вычислить столбец неизвестных Х.

Обратную матрицу можно вычислить двумя способами:

1. с помощью алгебраических дополнений;

2. применяя преобразования Гаусса G 1)-G 3).

Введем сначала еще одну операцию: транспонирования матриц.

Если то , т.е. при транспонировании столбцы матрицы А переписываются в виде строк матрицы А^Т.

Например,

.

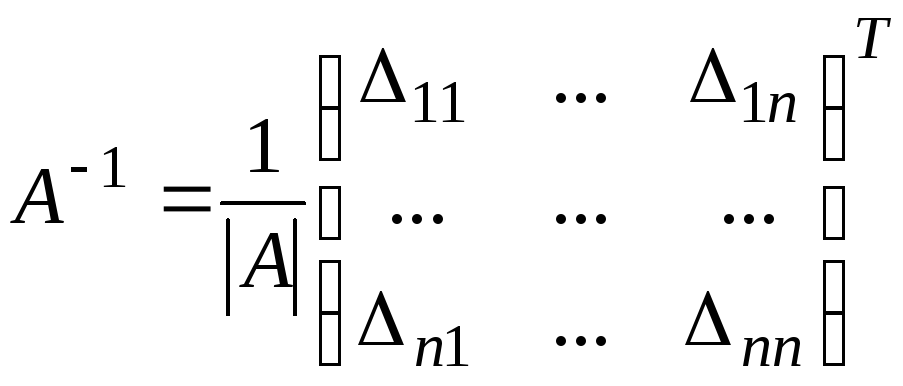
Теорема 1. Если А – квадратная матрица, |A|0, то

, (7)

где алгебраические дополнения _ij вычисляются по формуле (1).

Теорема 2. Если с помощью преобразований строк G 1)- G 3) матрица (А:Е) преобразуется в матрицу (Е:С), то С=А^-1.

Пример 3. Решить систему из примера 1 по формуле (6), вычисляя матрицу А^-1 двумя способами по формулам 1 и 2.

Решение. Вычислим для обратную матрицу по формуле (7). Из примера 2 имеем |А|=-5 по формулам (1) найдем 9 алгебраических дополнений:

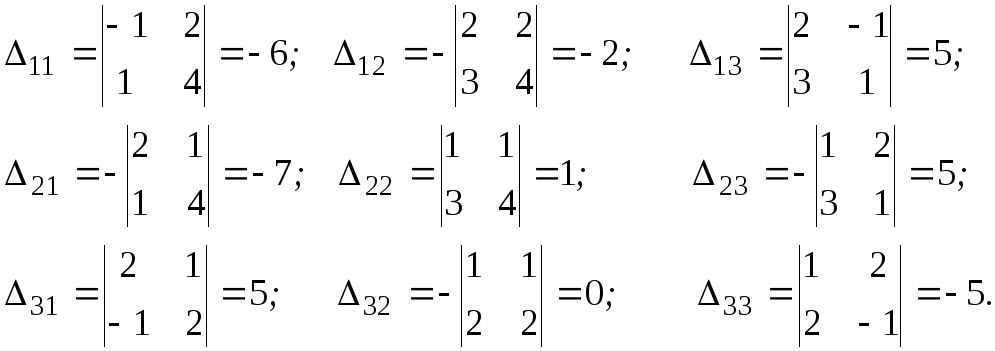
По формуле (7)

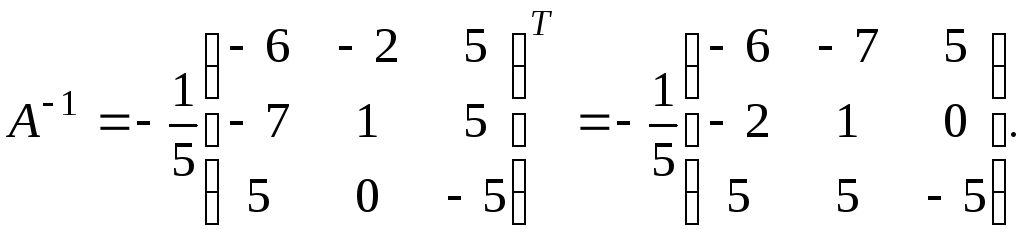(8)

По формуле (6)

, что совпадает с полученным ранее ответом.

Найдем теперь А^-1 по теореме 2:

т.е. 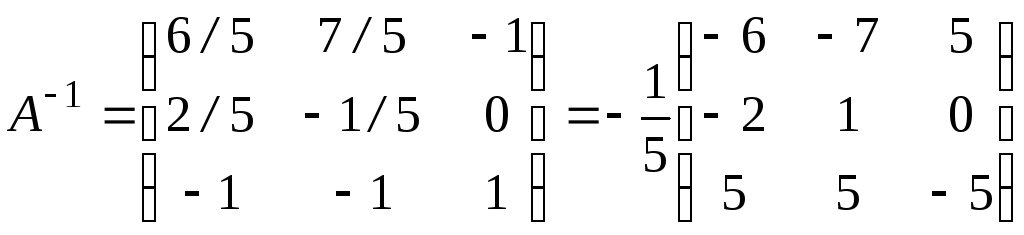, что совпадает с ответом (8).

Тема 2. Линейное пространство. Базисы. Координаты

Мы будем рассматривать только конечномерные линейные пространства L, один из базисов в которых ={е₁,…, e_n} указать легко. Так, например, в пространстве Veсt₂ , в пространстве многочленов степени не выше 2 ={1, x, x²}, в пространстве Rⁿ столбцов высоты n базис

.

Для любого аL существует единственный набор чисел а₁,…,а_n, такой, что

а=а₁е₁+а₂е₂+…+а_ne_n, (9)

столбец называется столбцом координат элемента, аL в базисе .

Если F={f₁,…,f_n} L, то определим матрицу

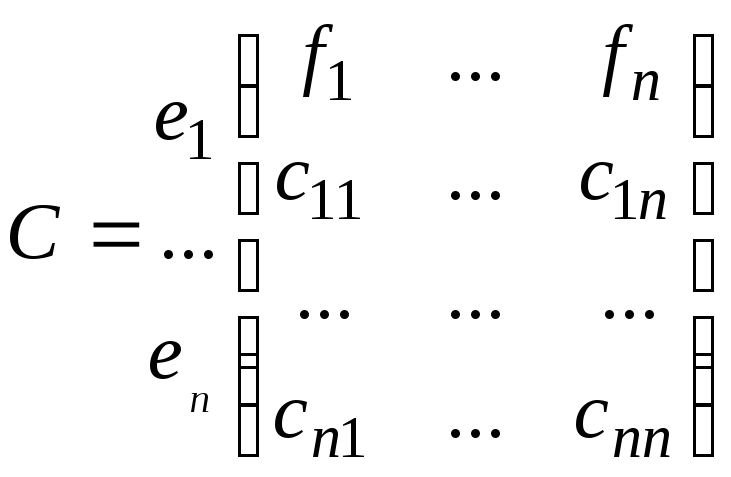, (10)

состоящую из - столбцов координат элементов f₁, …, f_n в базисе .

В случае |С|0 F является базисом L, а матрица (10) называется матрицей перехода от базиса  к базису F. Несложно доказать, что для любого аL

. (11)

Матрицей перехода от базиса F к базису  является обратная матрица С^-1. Из равенства (11) .

Пример 4. Проверить, что F={x²+1, 2x²-x, 2x-3} – базис пространства Р₂. Найти для а=х²+х+2.

Решение. Здесь стандартный базис ={1, x, x²},

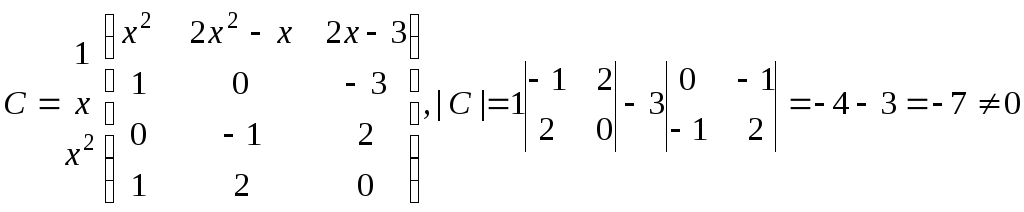поэтому F – базис пространства . Очевидно, что 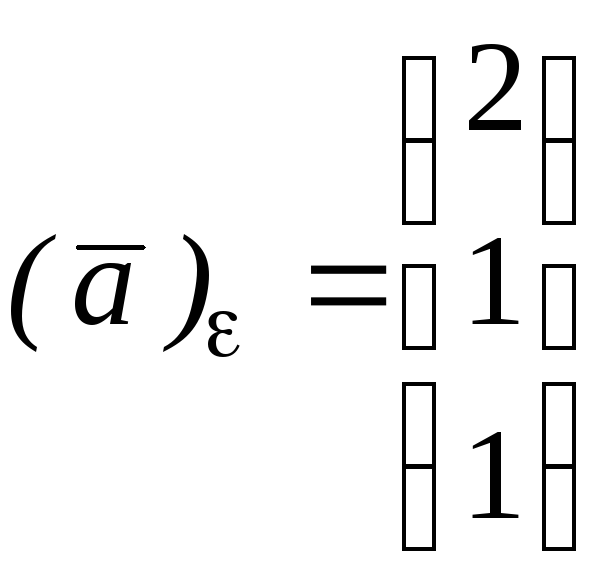, а тогда 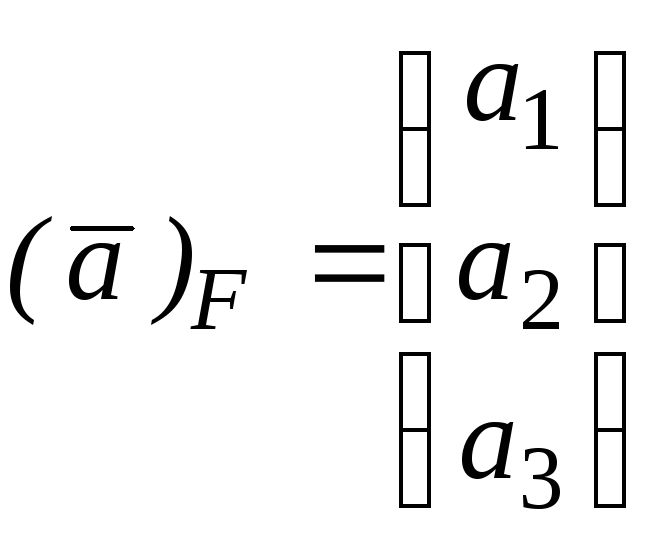можно найти, решая систему (11)

.

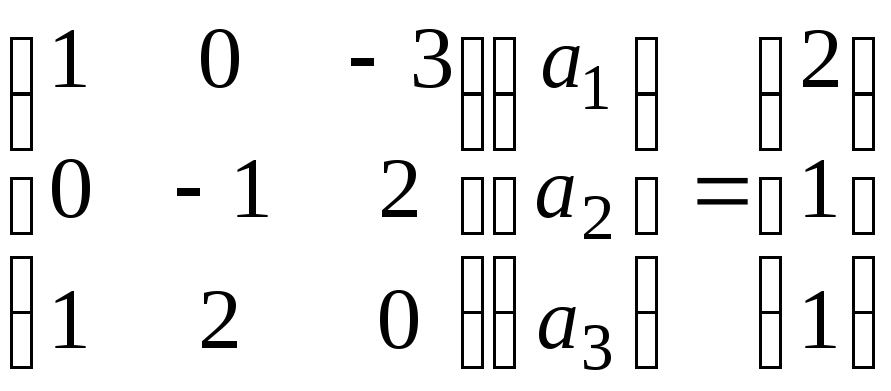Решим эту систему методом Гаусса:

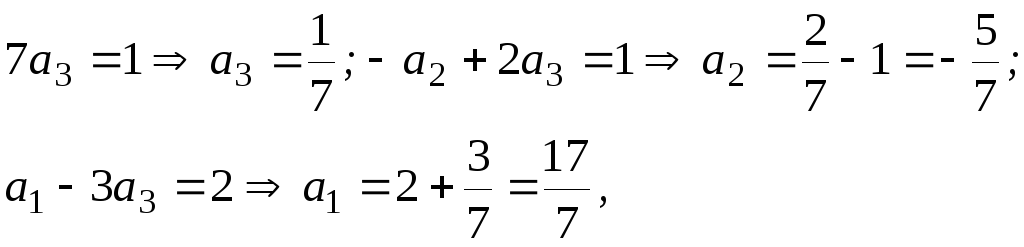
т.е.

.

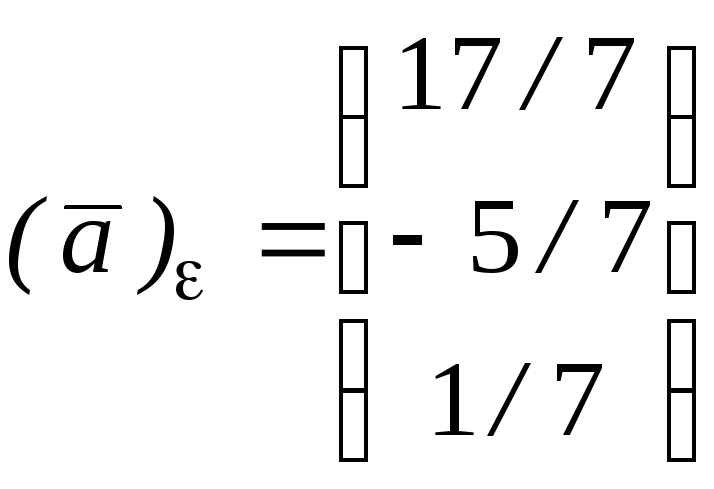Сделаем проверку: а=а₁f₁+а₂f₂+а₃ f₃, или

что верно.

Рассмотрим еще один важный пример.

В случае b₁=b₂=…=b_m=0 СЛАУ (3) называется однородной, ее матричная запись (4) имеет вид

АХ=0. (12)

Легко проверить, что множество всех столбцов ХRⁿ, удовлетворяющих равенству (12), образует линейное пространство Х₀₀Rⁿ (Х₀₀ – общее решение однородной системы).

Алгоритм нахождения базиса  пространства Х₀₀ начинается с приведения расширенной матрицы системы (12) (А:0) к ступенчатому виду с помощью преобразований Гаусса G1) – G3). Вторую часть алгоритма будет удобно рассмотреть на примере.

Пример 5. Найти общее решение Х₀₀ системы

. (13)

Решение. Расширенная матрица системы (13) уже имеет ступенчатый вид. «Лишние» переменные – х₄, х₅ (их называют вспомогательными). Базисными решениями Х₁ и Х₂ пространства Х₀₀ являются решения:

Х₁ : х₄=1, х₅=0,

Х₂ : х₄=0, х₅=1,

где одна из вспомогательных переменных равна 1, а остальные вспомогательные переменные равны 0. Вычислим поочередно Х₁ и Х₂. Для Х₁ из (13) при х₄=1, х₅=0 получим

,

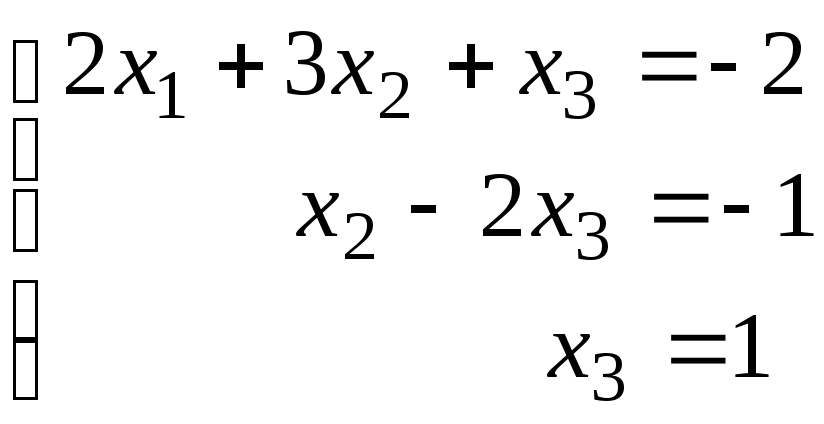Откуда , т.е.

. (14)

Для вычисления Х₂ из (13) при х₄=0, х₅=1 получим

,

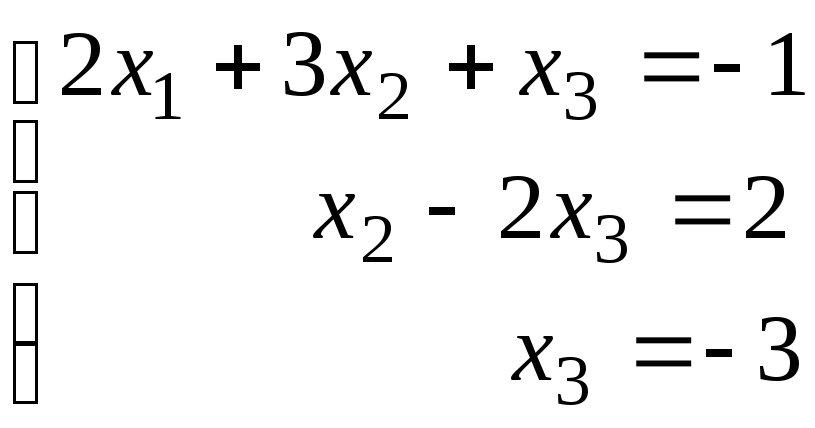Откуда ,

.

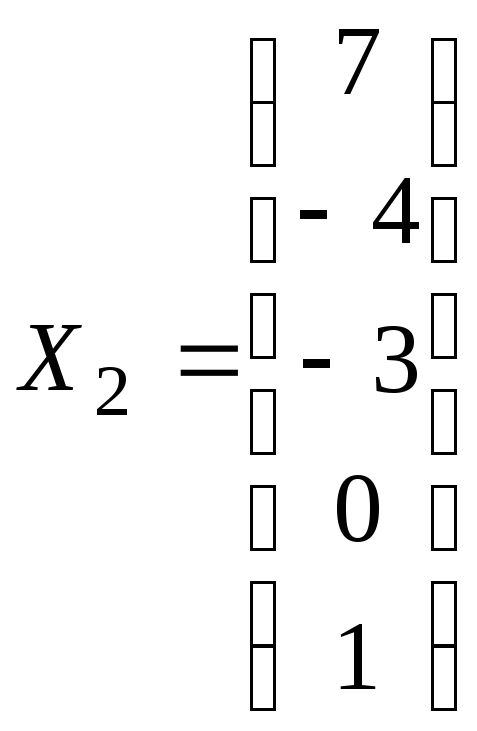Из (14) и (15) окончательно получим

, где С₁, С₂ – произвольные вещественные числа.