30

УТВЕРЖДАЮ

Ректор университета

__________ А.В. Лагерев

«___»____________2010г.

Алгебра и теория чисел

Методические указания

к выполнению самостоятельной работы

для студентов I курса очной формы обучения

специальности № 510503 «Математическое

обеспечение и администрирование

информационных систем»

(I семестр)

Брянск 2010

УДК 511

Математика: Методические указания к выполнению самостоятельной работы для студентов I курса очной формы обучения специальности № 510503 «Математическое обеспечение и администрирование информационных систем» (I семестр). – Брянск: БГТУ, 2010. - с.

Разработал: В.Х. Салихов, д.ф.-м.н., проф.

Рекомендовано кафедрой «Высшая математика» БГТУ (протокол № 1 от 31 августа 2010г.)

Предисловие

Данные методические указания предназначены для студентов, изучающих курс алгебры и теории чисел, и содержат теоретические сведения, а также практические задания для подготовки к контрольной работе, 30 вариантов расчетно-графической работы и необходимые материалы для подготовки к зачету. В этом пособии рассмотрены 6 тем, изучаемых в первом семестре.

Тема 1. Матрицы. Простейшие способы решения систем линейных алгебраических уравнений

Определение 1. Прямоугольной матрицей называется прямоугольная таблица чисел

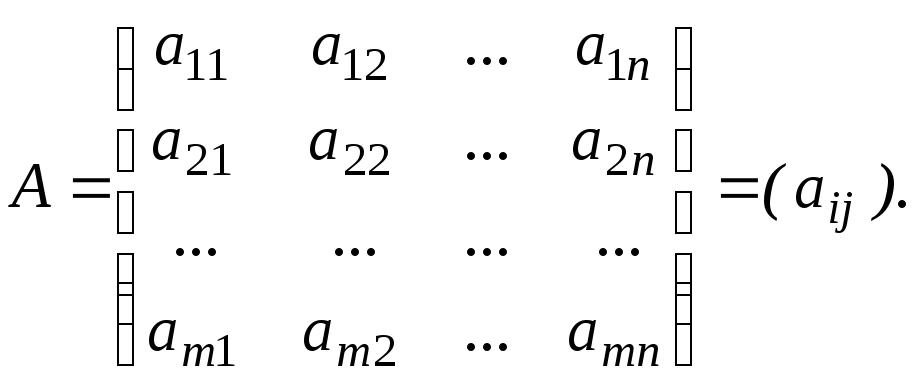
Если m=n, то А – квадратная матрица.

Важными примерами матриц являются::

1. Ступенчатая матрица - , где а₁₁0, а₂₂0,…, а_mm0, nm.

2. Диагональная матрица - .

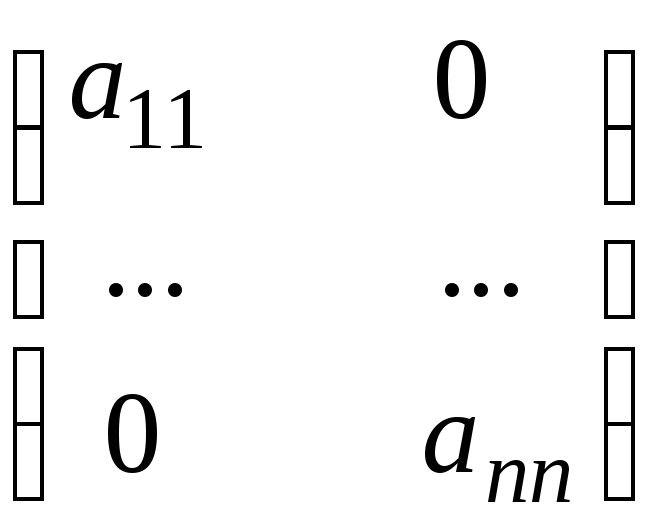3. Единичная матрица - .

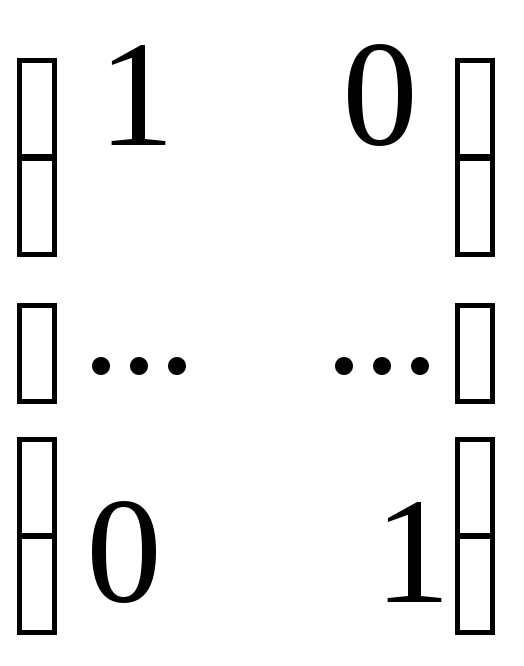Важнейшей операцией над матрицами является умножение

С=АВ=,

где А – матрица размера mn, В – матрица размера np, C – матрица размера mр, здесь и везде далее =(а_i1, а_i2,…, а_in); 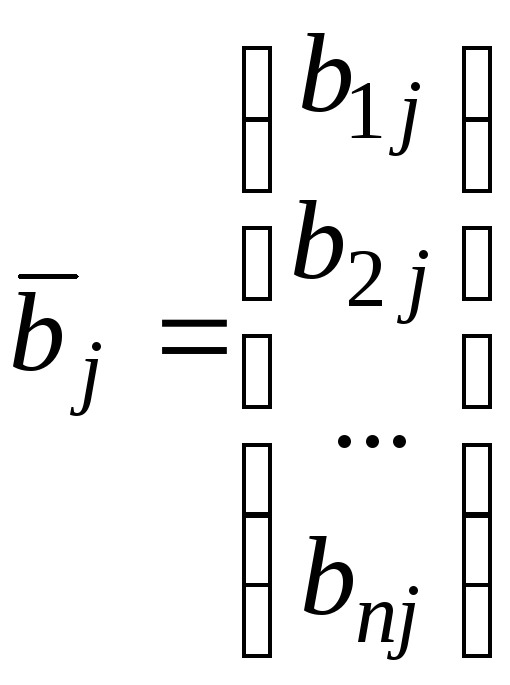, для всех i=1,…,m, j=1,…,p.

Легко привести примеры, когда АВВА. В то же время А(ВС)=(АВ)С, т.е. умножение матриц обладает свойством ассоциативности.

Важную роль играют следующие преобразования матриц:

G 1) перестановка строк (столбцов),

G 2) умножение строки на число ( =( а_i1,…, а_in)),

G 3) +, ij.

Для квадратной матрицы А рассмотрим |A| = detA – число, называемое детерминантом (определителем). Его удобно ввести рекуррентным способом, т.е. предположим, что мы умеем вычислять |A| для квадратной матрицы размера n-1.

Пусть А – квадратная матрица размера n,

_ij=(-1)^i+j|A_ij|, (1)

где A_ij – матрица, полученная из А вычеркиванием i-ой строки и j-го столбца. Число _ij называют алгебраическим дополнением элемента а_ij. Следующая формула позволяет вычислить |A|:

|A|=а₁₁₁₁+ а₁₂₁₂+…+ а_1n_1n. (2)

В частности, при n=1 для А=(а) |A|=а; при n=2

;

при n=3 по формуле(2)

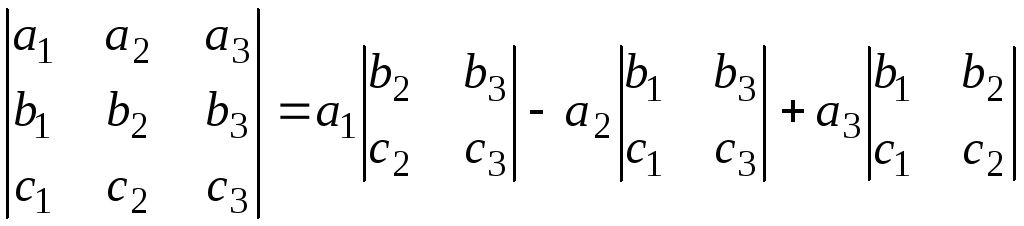=а₁(b₂c₃-b₃c₂)-а₂(b₁c₃-b₃c₁)+ а₃(b₁c₂-b₂c₁).

Подробным образом можно вычислять определители матриц произвольного размера.

Среди многочисленных свойств определителей отметим, что |A| можно вычислить аналогично (2), используя любую строку (столбец) матрицы А; при применении G 1) определитель меняет знак; после применения G 2) определитель умножается на число , а преобразование G 3) не изменяет значение определителя.

Одной из важнейших задач алгебры является решение систем линейных алгебраических уравнений (СЛАУ):

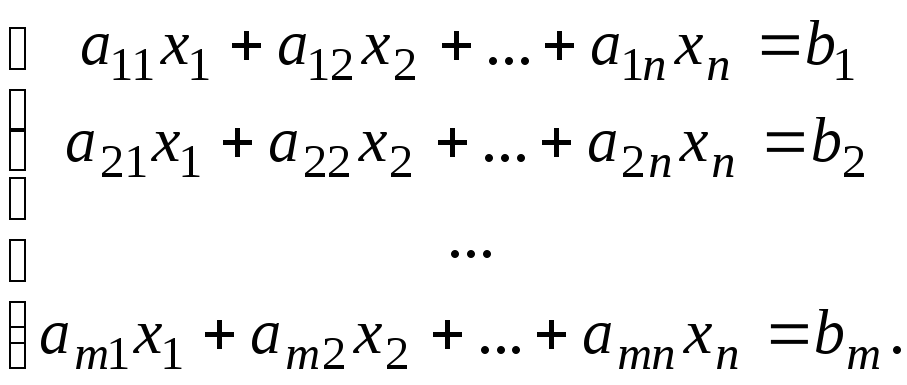(3)

Обозначим

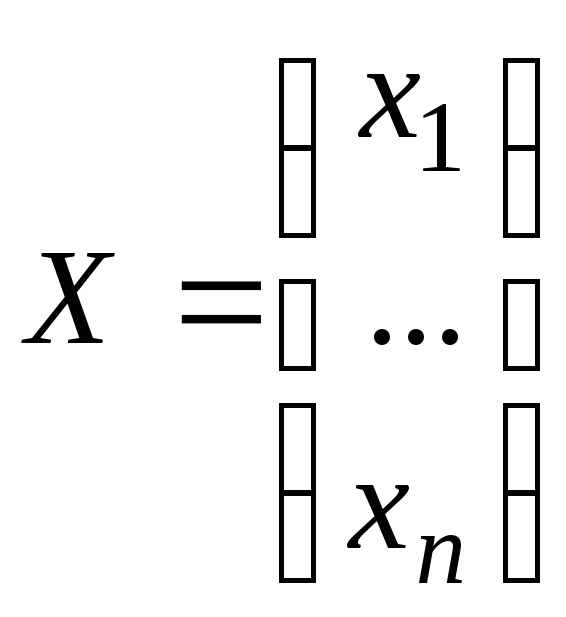- столбец неизвестных,

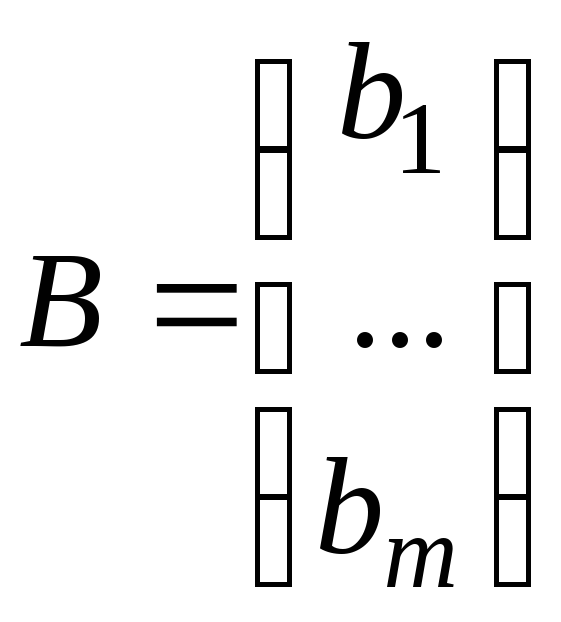- столбец свободных членов,

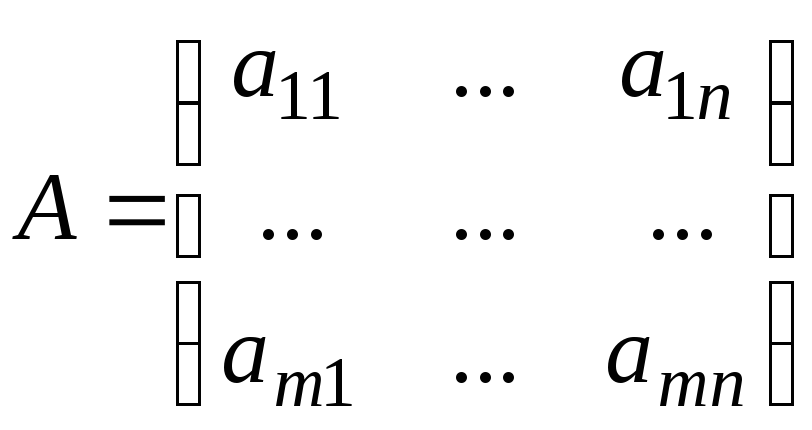- матрица системы.

Используя правило умножения матриц, СЛАУ (3) можно записать в матричном виде

АХ=В. (4)

Исследование систем (3) в общем виде проведем позже (см. тему 6). А пока ограничимся простейшим случаем, когда m=n, |A|0. В этом случае система (3) имеет единственное решение. Рассмотрим три метода решения СЛАУ.