Тема 3. Линейный оператор. Матрица в данном базисе. Собственные векторы и собственные значения

Определение 3. Матрицей линейного оператора Т в базисе  называется матрица

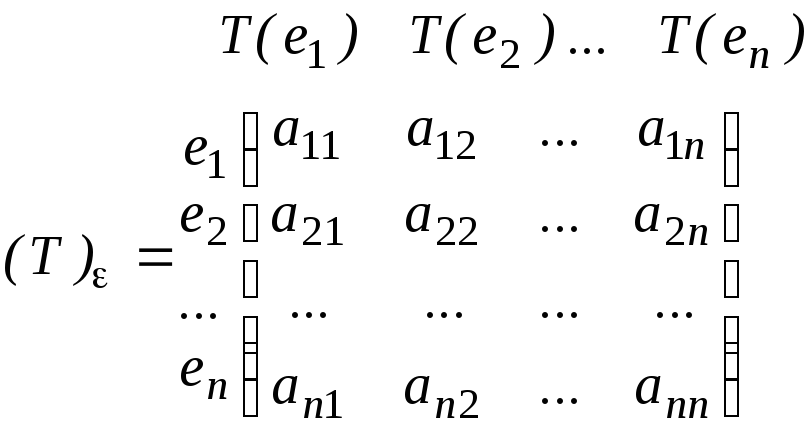, (16)

столбцы которой – столбцы координат векторов в базисе .

Мы рассмотрим два главных примера нахождения подобных матриц, имеющих отношение к основной задаче курса – решению СЛАУ (3).

Пусть L=Vect₃, , Т - оператор отражения относительно плоскости

П : Ах+Ву+Сz=0.

Для любого , где - нормальный вектор плоскости П, - проекция вектора на вектор .

Имеем

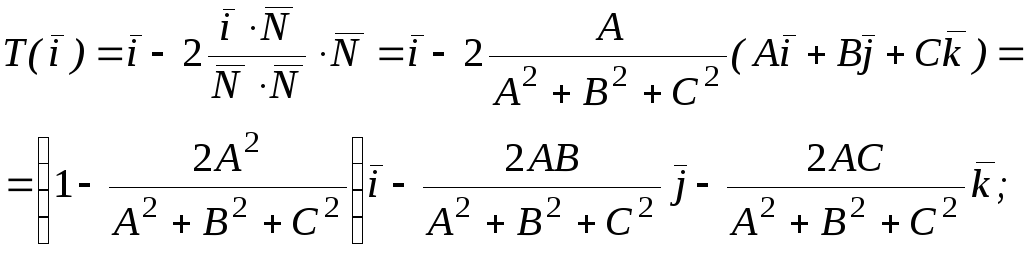
аналогично

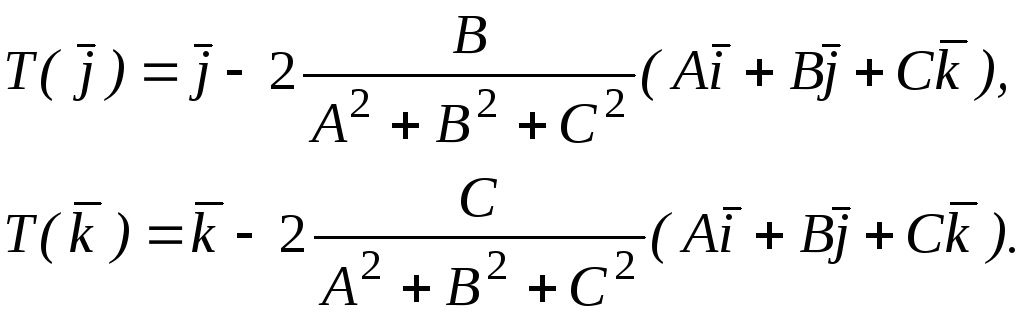
Поэтому по формуле (16), обозначая =А²+В²+С²:

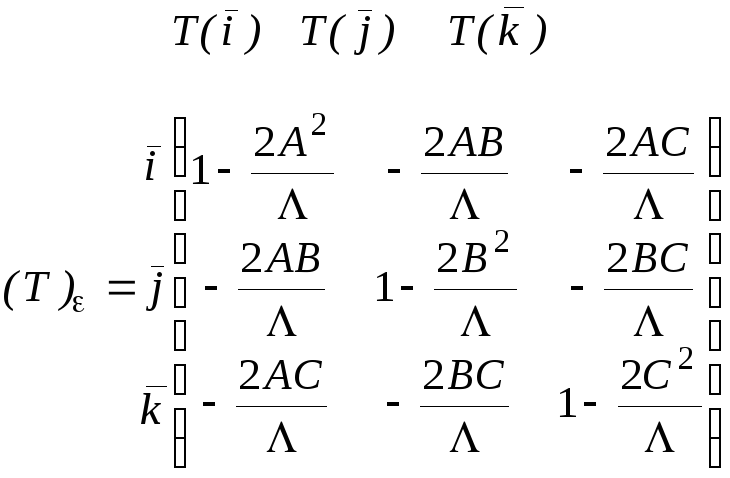. (17)

Матрица (17) называется матрицей отражения. Ее по аналогии несложно написать для L=Rⁿ.

Пусть теперь L=Vect₂, , Т - оператор поворота вектора на угол  относительно начала координат. Очевидно, .

По формуле (16)

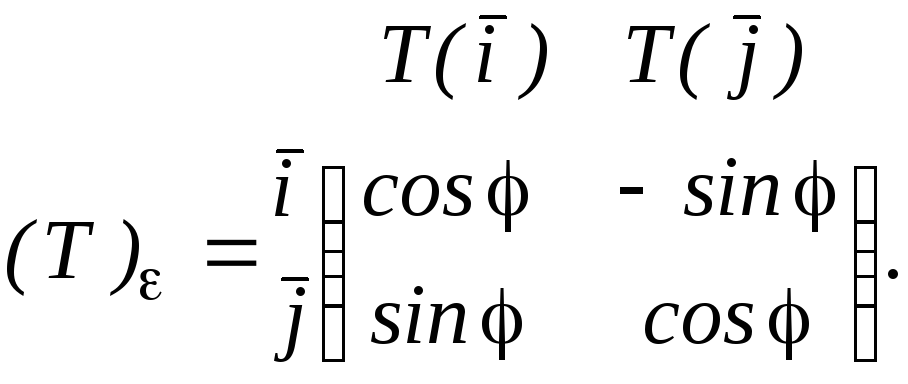(18)

Матрица (18) называется матрицей поворота.

Определение 4. Собственным вектором оператора Т, отвечающим собственному значению , называется ненулевой вектор такой, что

Т(а)=а. (19)

Так как для любого базиса , то равенство (19) можно записать в матричном виде

АХ=Х, (20)

где А=(Т)_, .

Из равенства (20) несложно получить равенство (А-Е)Х=0. Если | А-Е |0, то существует обратная матрица (А-Е)^-1, а тогда по формуле (6) при В=0 получим Х=( А-Е)^-10=0. Но Х0, поэтому необходимо

| А-Е |=0. (21)

Уравнение (21) называется характеристическим уравнением для матрицы А. Это уравнение является алгебраическим уравнением степени n. В случае, если это уравнение имеет n различных вещественных корней ₁, ₂, …, _n, то можно найти базис F={f₁,…, f_n}, состоящий из соответствующих собственных векторов (Т(f₁)=₁f₁,…, T(f_n)=_nf_n). А тогда

-

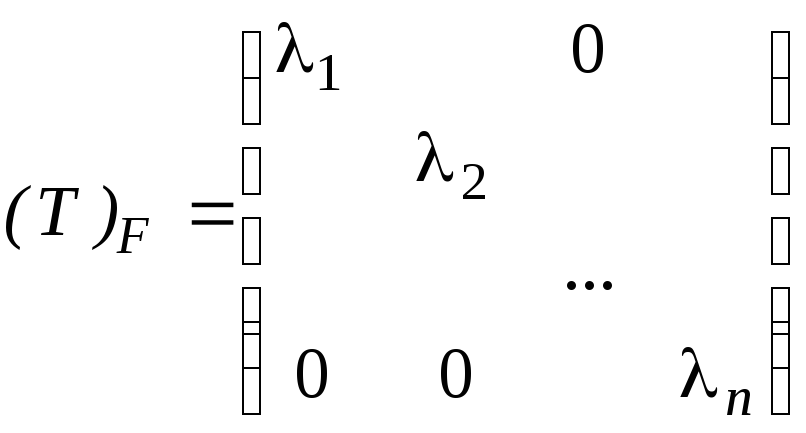- диагональная матрица. Эту ситуацию мы рассмотрим на примере в следующей теме (см. пример 9).

Тема 4. Функционалы

В этой теме мы рассмотрим три вида функционалов: линейные, билинейные и квадратичные.

1. Линейные функционалы

Определение 5. Отображение  : LR, где L – линейное пространство, называется линейным функционалом, если (a+b)=(a)+(b) для любых a,bL, (a)=(a) для любых аL, R.

Определение 6. Строкой координат линейного функционала  в базисе ={e₁,…, e_n} называется строка

. (22)

Пример 6. Найти строку координат линейного функционала , где , базис .

Решение. Применим формулу . Тогда

. По формуле (22) при n=3

2. Билинейные функционалы

Определение 7. Отображение  : LLR (т.е. (а,b)R для любых a,bL) называется билинейным функционалом, если выполняются четыре свойства линейности (см. определение 5):

1. (а₁+а₂, b)=(a₁, b)+(a₂, b);

2. (а, b)=(a, b);

3. (а, b₁+b₂)=(a, b₁)+(a, b₂);

4. (a, b)=(a, b).

Простейшим (и главным!) примером билинейного функционала является скалярное произведение векторов:

L=Vect₃, для .

Билинейный функционал (а, b) называется симметричным, если для всех а,bL выполняется равенство

( b, а)= (a, b).

В частности, скалярное произведение векторов является симметричным билинейным функционалом, т.к. .

Определение 8. Матрицей билинейного функционала (a, b) в базисе ={e₁,…, e_n} называется матрица вида

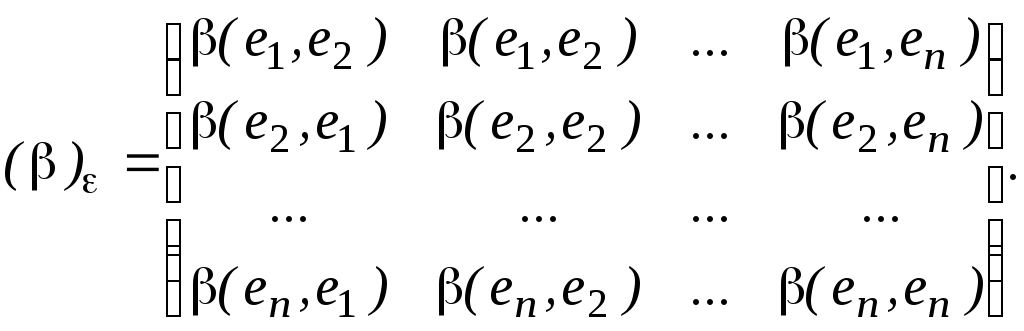(23)

Для симметричного билинейного функционала матрица (23) является симметричной. Справедлива следующая теорема, с помощью которой можно вычислить значение (a, b).

Теорема 3. Справедлива формула

(24)

где  - произвольный базис линейного пространства L, (a, b) – билинейный функционал, a, bL.

Нам далее будет полезна еще одна теорема, позволяющая вычислять матрицы линейного оператора и билинейного функционала при заменах базисов.

Теорема 4. Справедливы формулы

(Т)_F=С^-1(Т)_С, (25)

()_F=С^Т()_С, (26)

где С – матрица перехода от базиса  к базису F, вычисленная по формуле (10).

Формулы (25) и (26) весьма похожи и просто совпадают, если С^-1=С^Т.

Определение 9. Матрица С называется ортогональной, если выполняется равенство

С^-1=С^Т. (27)

Итак, если С – ортогональная матрица, то матрицы линейного оператора и билинейного функционала при переходе к новому базису преобразуются одинаково.