Решение

Вычерчиваем расчетную схему (рис. 16, а).

1. Определение реакций опор. Запишем уравнения равновесия:

, ,

;

, ,

.

Проверка: ,

,

2. Построение эпюр и . Разобьём балку на три участка и составим аналитические выражения изгибающего момента и поперечной силы .

Рис.16

I участок (),

(),

.

II участок (),

(квадратичная парабола),

 при , ,

 при , ;

(линейный закон),

 при , ,

 при , .

При изгибающий момент принимает наибольшее значение:

, ;

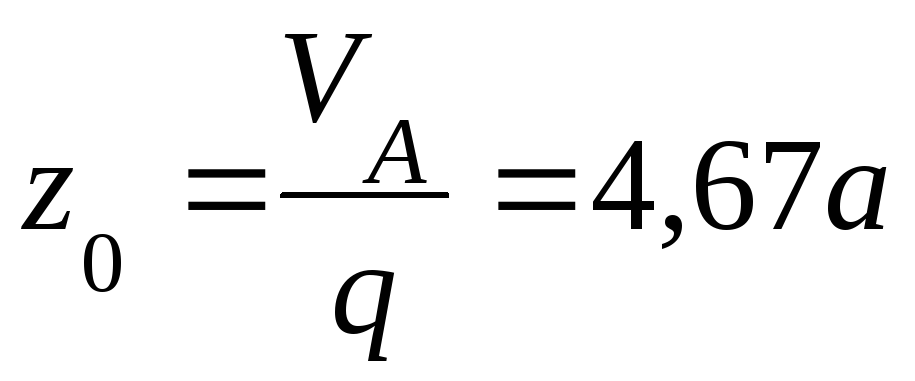II участок (),

(линейный закон),

 при , ,

 при , ;

().

По найденным значениям и строим эпюры (рис. 16, б, в). По эпюрам находим:

, .

3. Определение несущей способности балки.

Запишем условие прочности по нормальным напряжениям:

, или ,

откуда Н/м кН/м.

4. Проверка прочности балки по касательным напряжениям.

Условие прочности:

,

Па МПа.

Подставляем в условие прочности:

МПа МПа,

т.е. прочность балки по касательным напряжениям обеспечена.

Ответ: несущая способность балки кН/м; прочность по касательным напряжениям в опасном сечении обеспечена.

Задача 7. Косой изгиб бруса*

Для стальной балки АВ (рис. 17), загруженной в главных плоскостях силами и , т р е б у е т с я:

1. Определить размеры поперечного сечения

(табл. 9).

2. Найти значение полного прогиба и указать его направление:

• для консольной балки – в середине её длины;

• для балки на двух опорах – в середине её пролета.

Исходные данные взять из табл. 9.

П о р я д о к р а с ч ё т а

1. Вычертить в масштабе расчётную схему балки и её поперечное сечение.

2. Построить эпюры изгибающих моментов и в главных плоскостях инерции.

3. Установить по эпюрам и опасное сечение балки.

4. Определить размеры поперечного сечения из условия прочности. Принять расчетное сопротивление материала изгибу МПа; коэффициент условий работы .

5. Вычислить для указанного сечения прогибы и в главных плоскостях. Принять модуль продольной упругости МПа.

6. Найти величину полного прогиба f и указать его направление.

Таблица 9

Номер строки	Схема балки, рис. 17		, м	, кН		, кН	Форма сечения балки
1	1		3,0	30		20	h = 3b
2	2		3,2	40		30
3	3		3,4	50		20	h = 4b
4	4		3,6	60		40
5		5	3,8		50	30	h = 1,8b
6		6	4,0		70	40
7		7	4,2		30	60	h = 0,5b
8		8	4,2		40	50

Продолжение таблицы 9

9	9	4,6	80	40
0	0	4,8	90	60
	д	е	г	а	е

Пример 7. Балка АВ заданного поперечного сечения (рис. 18 а, б), загружена силами , , , направленными по главным центральным осям поперечного сечения.

Т р е б у е т с я:

1. Построить эпюры изгибающих моментов и в главных плоскостях инерции.

2. Определить геометрические характеристики поперечного сечения балки.

3. По эпюрам 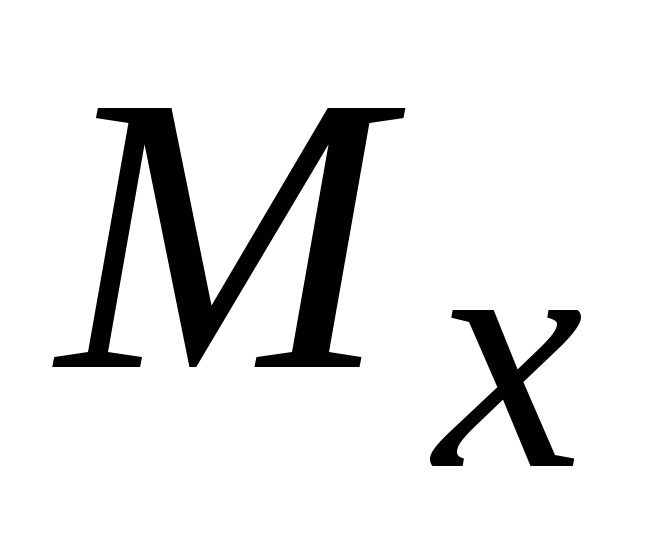и найти опасное сечение балки.

4. Определить размеры поперечного сечения из условия прочности.

5. Определить прогиб балки в середине её пролета С и указать его направление.

Д а н о: длина пролёта балки м; кН, кН, кН. Расчётное сопротивление материала изгибу МПа; модуль продольной упругости МПа; коэффициент условий работы .

а	б
Рис. 18