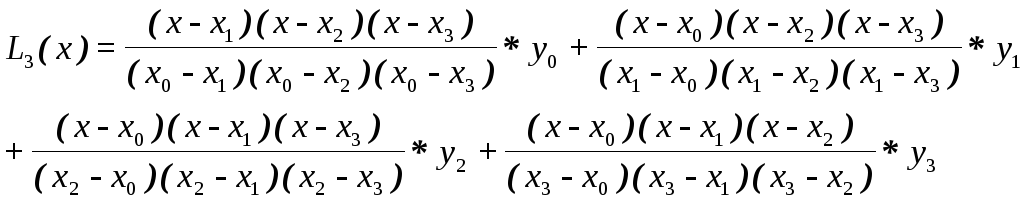1.2. Построение интерполяционного многочлена в форме Лагранжа.

Интерполяционный многочлен в форме Лагранжа (обозначим ) есть иная форма записи алгебраического многочлена :

Из определения интерполяционного многочлена следует, что функции должны обладать следующими свойствами:

1. ,

2. при ,

т. е. в узлах интерполяции интерполяционный многочлен совпадает с заданными значениями .

Таким образом, есть многочлен степени , для которого все узлы являются корнями. Тогда

(2.6)

Подставим в (2.6) любой узел кроме и убедимся, что для любого . Коэффициент выберем из следующих соображений:

или

Тогда

Интерполяционный многочлен в форме Лагранжа:

(2.7)

Числитель формулы (2.7) представляет собой произведение разностей между переменной x и всеми узлами, кроме i-го, а знаменатель – произведение разностей между i-м узлом и всеми остальными.

Пример.

Для прежних исходных данных многочлен Лагранжа (2.7) будет иметь вид:

(2.8)

Если подставить исходные данные в (2.8), раскрыть скобки и привести подобные члены в полученном выражении, то получим тот же многочлен в канонической форме:

Найдем , подставив x₄, x₅ в (2.8):

1.3. Построение интерполяционного многочлена в форме Ньютона.

Интерполяционный многочлен в форме Ньютона имеет вид:

(9)

где - произвольная сетка узлов интерполяции; - неизвестные пока коэффициенты.

Для определения воспользуемся критерием интерполяции:

{0,1,…,n}.

(10)

Условия (2.10) приводят к системе уравнений:

(11)

Уравнения (11) представляют собой СЛАУ с нижней треугольной матрицей, которая легко решается прямой подстановкой: из первого уравнения системы (11) определяется , затем подставляется во второе уравнение для нахождения и т.д.

Для вычисления значения многочлена используется модифицированная схема Горнера:

(12)

Пример.

Используя данные примера, получаем:

Используя формулу (9), построим многочлен Ньютона:

Найдем при тех же значениях x₄, x₅, используя модифицированную схему Горнера (12):

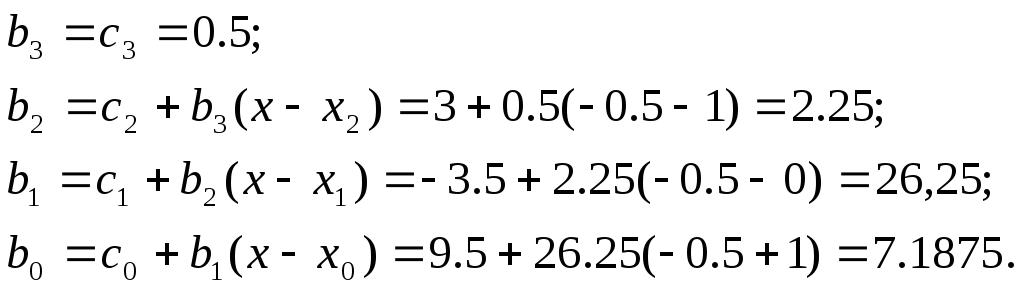
Интерполяционные многочлены - это разные формы записи одного и того же алгебраического многочлена.

1.4. Задание на практику.

Исходные данные представляют собой набор точек: , где -значение некоторой функции f(x) в узлах .

1. Построить интерполяционный алгебраический многочлен P_n(x), значения которого в узлах x_i совпадают со значениями функции y_i.

2. Используя схему Горнера, найти значения P_n(x) в точках x₄, x₅.

3. Построить интерполяционный многочлен в форме Лагранжа L_n(x).

4. Построить интерполяционный многочлен в форме Ньютона N_n(x).

5. Используя схему Горнера для формулы Ньютона, рассчитать значения многочлена в точках x₄, x_5.

6. Построить график функции P_n(x), используя значения функции в точках x_i, .