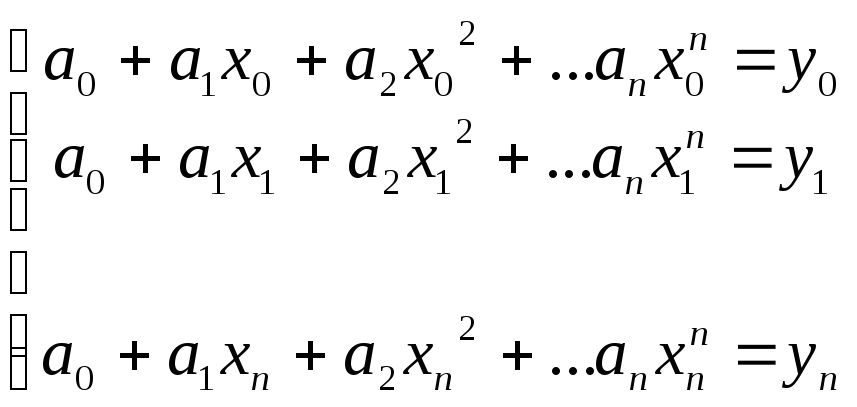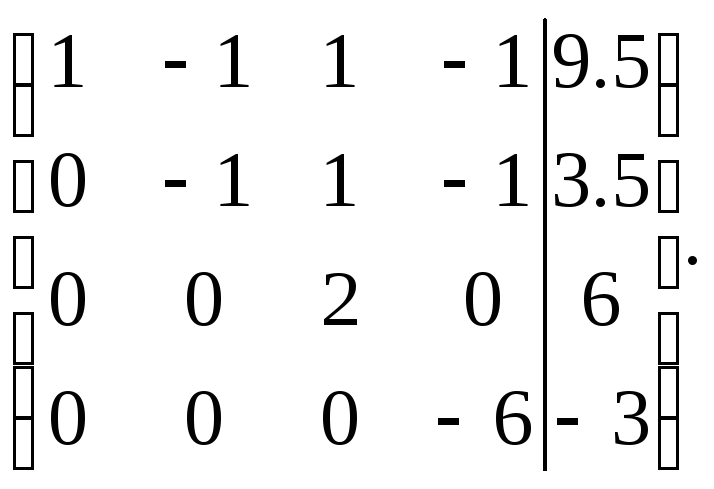11

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«Уральский федеральный университет имени первого Президента России Б.Н.Ельцина»

Институт радиоэлектроники и информационных технологий - РТФ

Кафедра Автоматика и информационные технологии

Полиномиальная интерполяция

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К лабороторной работе ПО ДИСЦИПЛИНЕ «Численные методы»

2011

Составитель И.А.Селиванова, ст.преподаватель.

ПОЛИНОМИАЛЬНАЯ ИНТЕРПОЛЯЦИЯ: Методические указания к практическим занятиям по дисциплине «Численные методы»

Указания предназначены для студентов всех форм обучения направления 230100 – «Информатика и вычислительная техника».

Ó ФГАОУ ВПО «УрФУ имени первого Президента России Б.Н.Ельцина», 2011

СОДЕРЖАНИЕ

1. ПОЛИНОМИАЛЬНАЯ ИНТЕРПОЛЯЦИЯ 4

1.1. Интерполяционный многочлен в канонической форме. 4

1.2. Построение интерполяционного многочлена в форме Лагранжа. 6

1.3. Построение интерполяционного многочлена в форме Ньютона. 7

1.4. Задание на практику. 8

1.5. Варианты заданий. 9

Список литературы 11

1. Полиномиальная интерполяция

Задача интерполирования состоит в том, чтобы по значениям функции f(x) в нескольких точках отрезка [a, b] восстановить ее значения в любой точке отрезка.

Пусть в точках x₀, x₁,…x_n таких, что <<…<, известны значения функции , т.е. на отрезке [a, b] задана табличная (сеточная) функция:

X … Y …

(1)

Функция называется интерполирующей или интерполяционной для на [a, b], если ее значения , ,…, в заданных точках , ,…, , называемых узлами интерполяции, совпадают с заданными значениями функции , т.е. с , ,…, соответственно. Будем считать, что интерполяционная функция есть многочлен степени n. Тогда задача интерполяции (полиномиальной, алгебраической или параболической, поскольку график любого многочлена называется параболой) формулируется следующим образом:

для функции , заданной таблицей (2.1), найти многочлен такой, что выполняется совокупность условий интерполяции:

{0,1,…,n}.

(2)

Найти многочлен - это значит, учитывая его каноническую форму

(3)

найти n+1 коэффициент a₀, a₁,…a_n .

1.1. Интерполяционный многочлен в канонической форме.

Чтобы многочлен (2.3) был интерполяционным для функции (1), нужно, чтобы его коэффициенты a₀, a₁,…a_n удовлетворяли системе уравнений

(4)

Из курса алгебры известно, что определитель этой линейной системы (так называемый определитель Вандермонда) отличен от нуля, т.е. решение этой системы существует и единственно.

Для вычисления значения многочлена в произвольной точке x используется схема Горнера (или схема вложенных умножений).

Для произвольного значения n интерполяционный многочлен в канонической форме имеет вид:

Для вычисления значения этого многочлена в произвольной точке рассчитываются вспомогательные коэффициенты

(5)

Значение в точке равно значению коэффициента b₀.

Пример.

Исходные данные:

i	0	1	2	3	4	5
	-1	0	1	2	-0.5	1.5
	9.5	6	8.5	20	-	-

Построим расширенную матрицу системы уравнений (4):

После приведения к треугольной форме получим:

Теперь можно найти :

Подставим полученные значения в формулу (2.3):

Используя схему Горнера (2.5), рассчитаем значения в точках

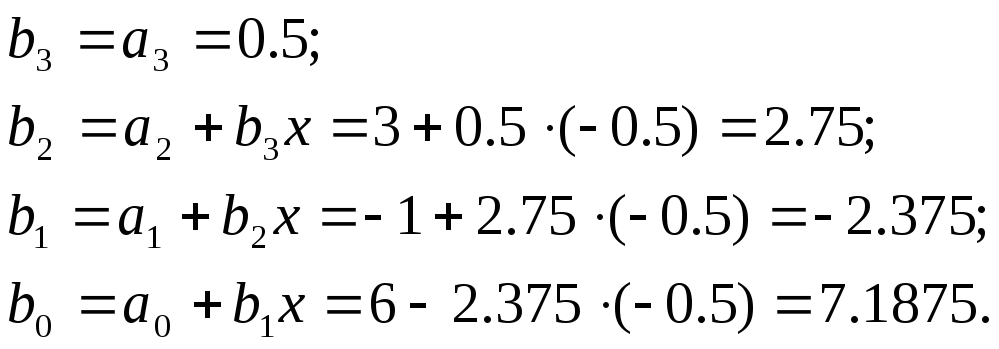
Значение =

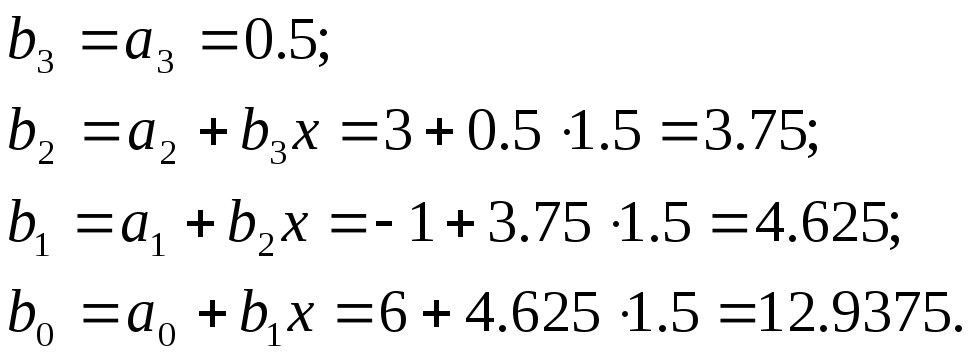
Значение =