
- •Сборник заданий по математике
- •Содержание Требования к оформлению контрольных работ ...................................... 2
- •Раздел 1. Линейная алгебра .................….............................................. 3
- •Список учебной литературы ...................................................................... 24 Требования к оформлению контрольных работ
- •Формирование исходных данных к задачам
- •1. Линейная алгебра
- •2. Аналитическая геометрия
- •3. Дифференциальное исчисление.
- •Интегральное исчисление.
- •Функции нескольких переменных.
- •Двойные, тройные и криволинейные интегралы.
- •Элементы теории поля.
- •Дифференциальные уравнения.
- •Функции комплексного переменного.
- •Операционное исчисление.
- •Теория вероятностей.
- •Случайные величины.
- •Элементы математической статистики
- •Линейное программирование.
- •Задача оптимального производства продукции.
- •Транспортная задача.
- •Матричные игры.
- •Математические методы в экономике.
- •Сетевое планирование.
- •Системы массового обслуживания (смо).
- •Задача межотраслевого баланса.
- •Дискретная математика.
- •Двоичная система счисления.
- •Логика высказываний.
- •Краткое содержание (программа) курса
- •I. Линейная алгебра.
- •2. Аналитичеcкая геометрия.
- •3. Дифференциальное исчисление.
- •4. Интегральное исчисление.
- •5. Функции нескольких переменных.
- •6. Двойные, тройные и криволинейные интегралы.
- •7. Элементы теории поля.
- •Список учебной литературы
-
Матричные игры.
-
Игра
 задана матрицей
задана матрицей
![]()
Найти вероятности применения стратегий 1-м и 2-м игроком для получения цены игры. (Задачу решить аналитическим методом.)
-
Игра задана матрицами
![]() для
для
![]() - четного
- четного
и
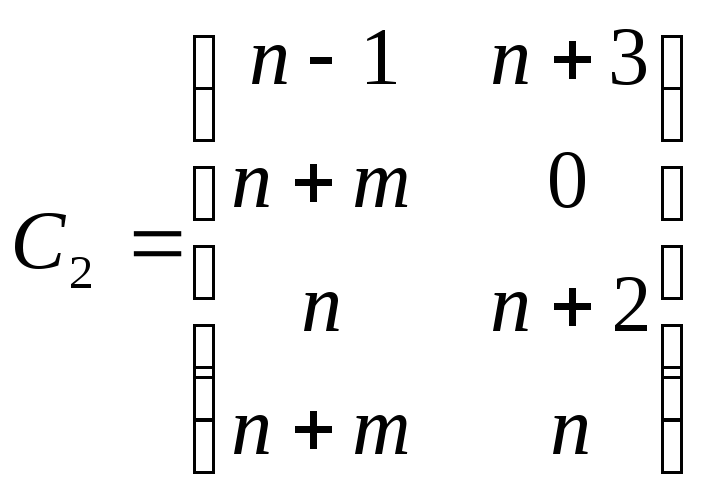 для
для
![]() - нечетного.
- нечетного.
Применяя графический метод, найти смешанные оптимальные стратегии обоих игроков и определить цену игры.
-
Математические методы в экономике.
-
Сетевое планирование.
Прогресс
производства сложной продукции
разбивается на отдельные этапы,
зашифрованные номерами 1, 2,..., 10. 1 –
начальный этап производства продукции,
10 – завершающий. Переход от
![]() -го
этапа к
-го
этапа к
![]() -му
этапу назовем операцией. Возможны
выполнения операций
-му
этапу назовем операцией. Возможны
выполнения операций
![]() и их продолжительности
и их продолжительности
![]() задаются таблицей.
задаются таблицей.
-
N
п/п
шифр операции
продолжительность операции
15.1.1. Составьте и упорядочите по слоям сетевой график производства работ. Номера этапов необходимо обвести кружками, а операции
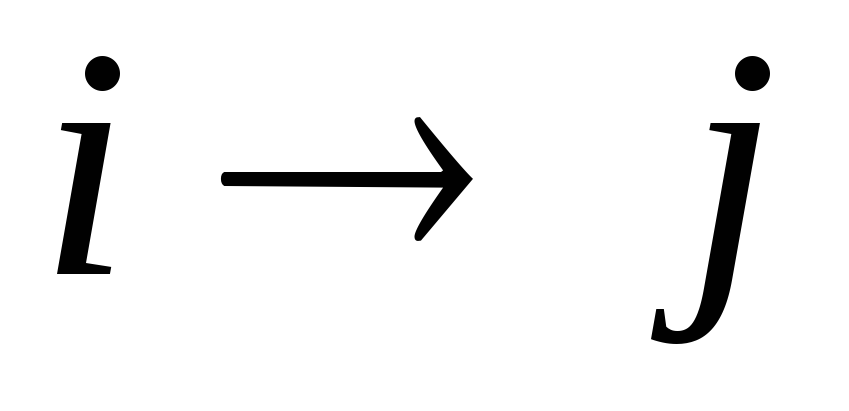 обозначить стрелками, проставляя над
ними продолжительность
обозначить стрелками, проставляя над
ними продолжительность
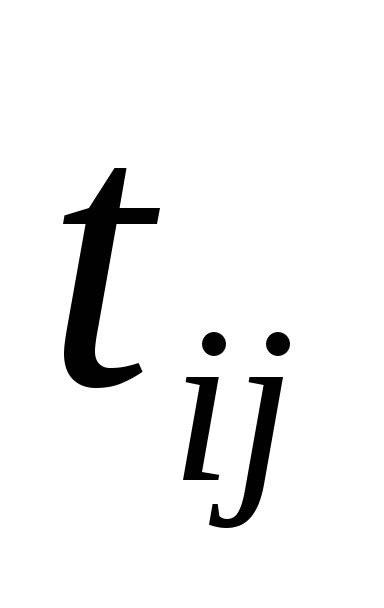 операции.
операции.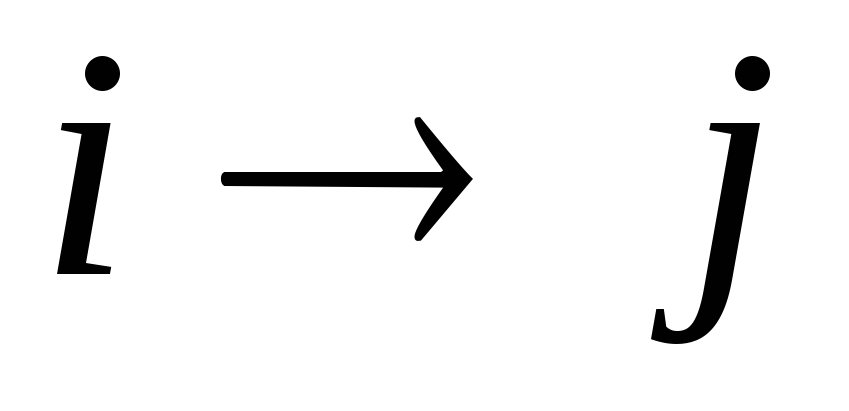
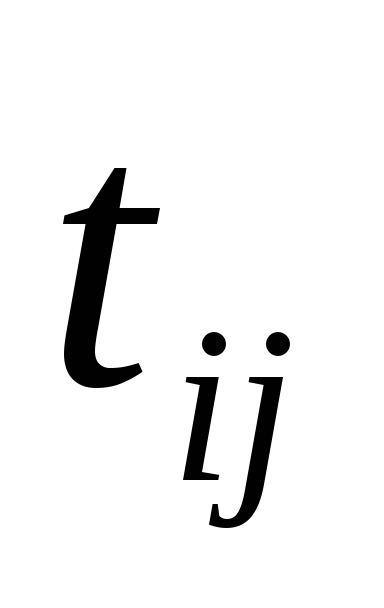
1
1→2
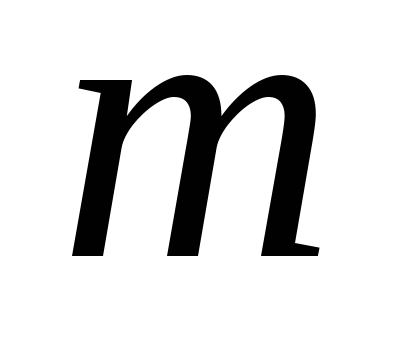
2
1→3
4
3
1→4
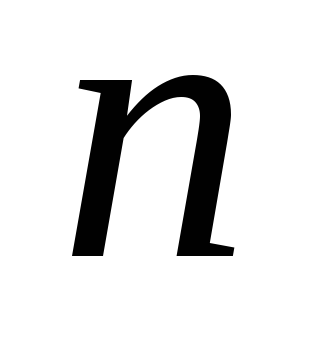
4
2→3
3
5
2→6
5
6
4→3
2
7
4→6
6
8
3→5
3
15.1.2. Считая, что начало работы происходит во время
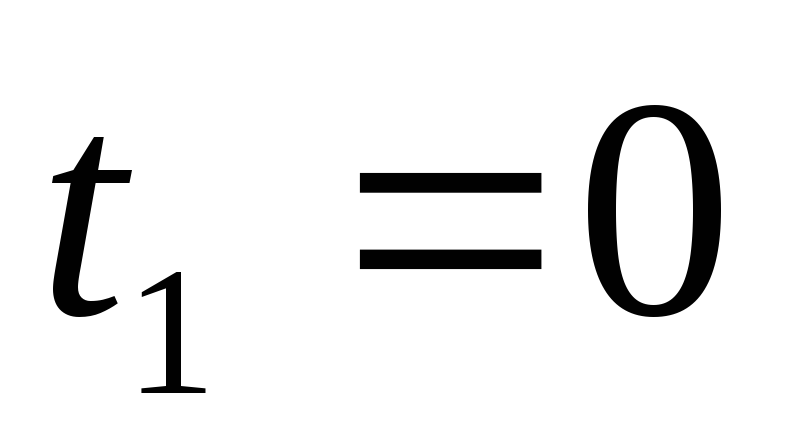 ,
определите время
,
определите время
 окончания каждого
окончания каждого
 -го
этапа и проставьте его над соответствующим
кружком.
-го
этапа и проставьте его над соответствующим
кружком.9
3→7
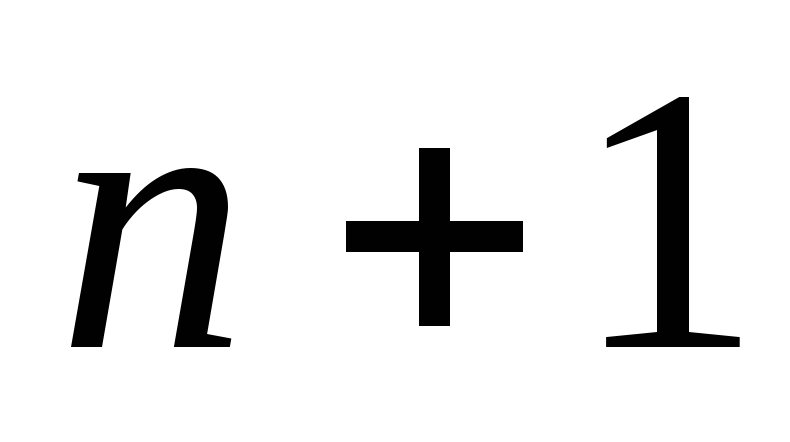
10
5→9
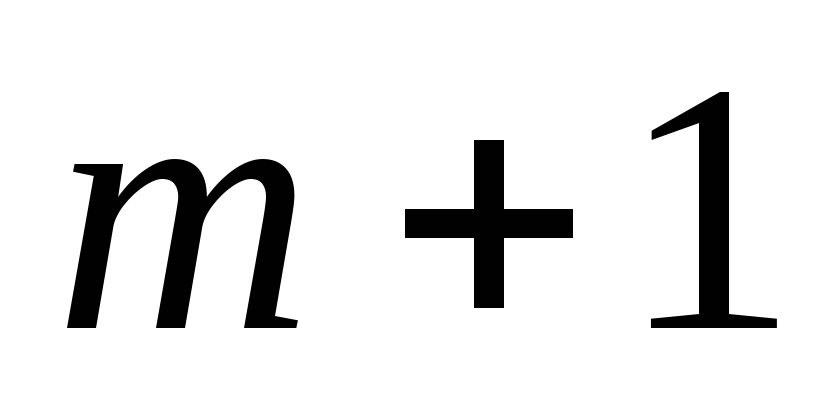
11
6→7
4
12
6→8
3
13
7→8
7
14
7→9

15
7→10
5
16
8→10
4
17
9→10
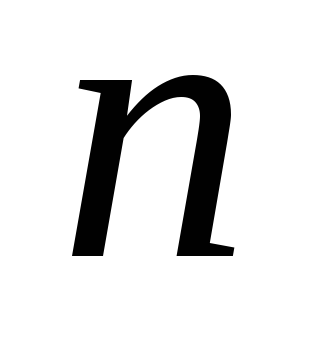
-
Найдите критическое время завершения процесса работ Ткр и выделите стрелки, лежащие на критическом пути.
-
Для каждой некритической операции
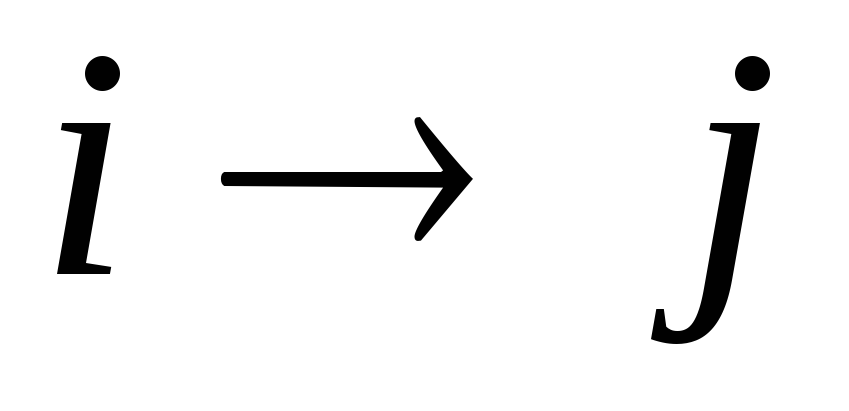 определите резервы свободного времени
определите резервы свободного времени
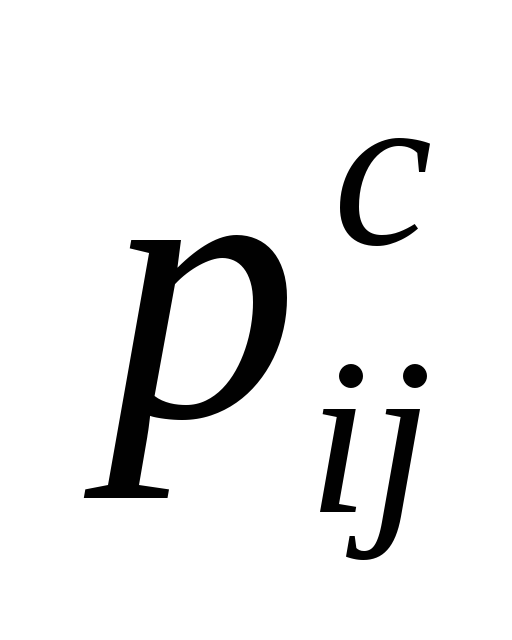 и проставьте их над стрелками рядом
с
и проставьте их над стрелками рядом
с
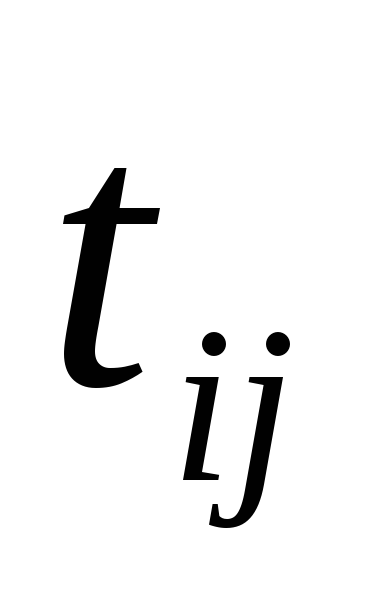 в скобках.
в скобках. -
Решите задачу табличным методом. Номера этапов, лежащие на критическом пути подчеркните. (В табличном методе кроме резервов свободного времени
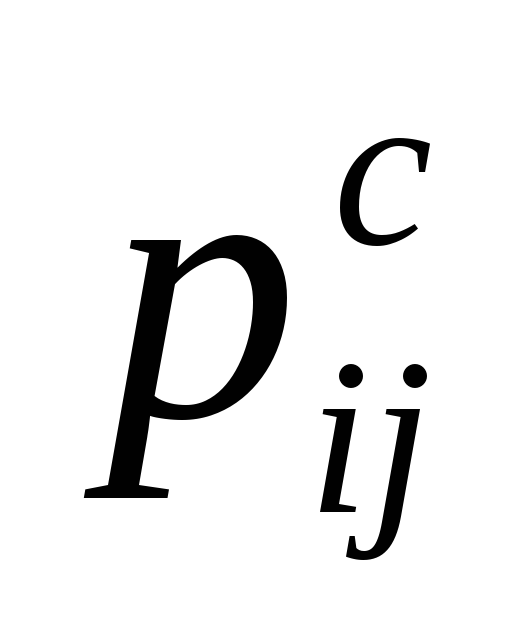 необходимо также найти полные резервы
времени
необходимо также найти полные резервы
времени
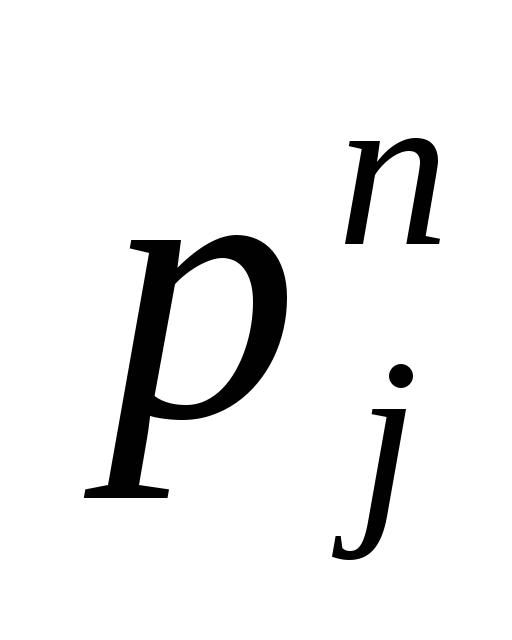 для каждого этапа.)
для каждого этапа.)
-
Системы массового обслуживания (смо).
В
парикмахерский салон приходит в среднем
![]() клиента в час (т.е. интенсивность
клиента в час (т.е. интенсивность
![]() поступления заявок в систему равна
поступления заявок в систему равна
![]() /час),
а среднее время обслуживания одного
клиента равно 1/
/час),
а среднее время обслуживания одного
клиента равно 1/![]() часов. Содержание одного рабочего места
обходится в
часов. Содержание одного рабочего места
обходится в
![]() тысяч рублей за 1 час, а доход от
обслуживания одного клиента составляет
тысяч рублей за 1 час, а доход от
обслуживания одного клиента составляет
![]() тысяч рублей в час.
тысяч рублей в час.
-
Найти относительную пропускную способность СМО
 (т.е. вероятность того, что поступившая
заявка будет обслужена) и абсолютную
пропускную способность СМО
(т.е. вероятность того, что поступившая
заявка будет обслужена) и абсолютную
пропускную способность СМО
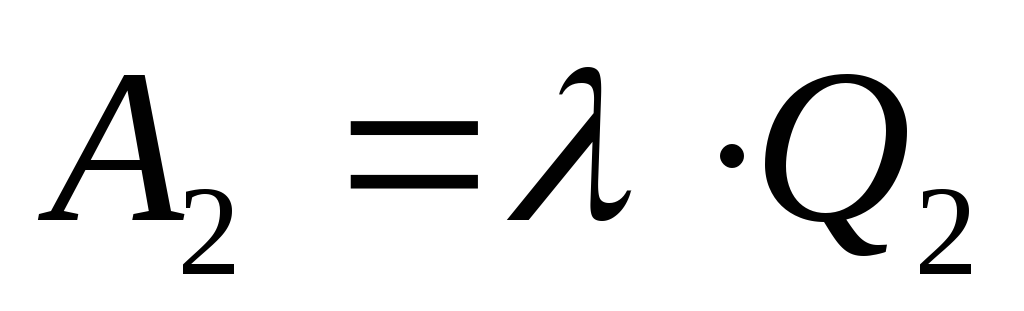 (число заявок, обслуживаемых за 1 час),
если салон обслуживает два мастера.
(число заявок, обслуживаемых за 1 час),
если салон обслуживает два мастера. -
Найти доход
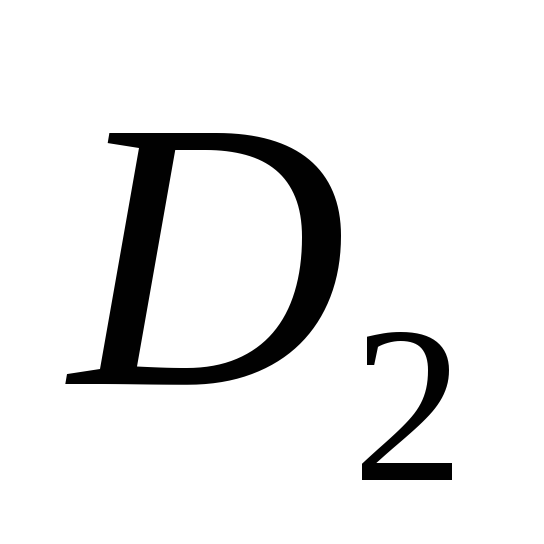 ,
полученный за 1 час работы двух мастеров.
,
полученный за 1 час работы двух мастеров. -
Найти аналогичные характеристики СМО
 ,
,
 и
и
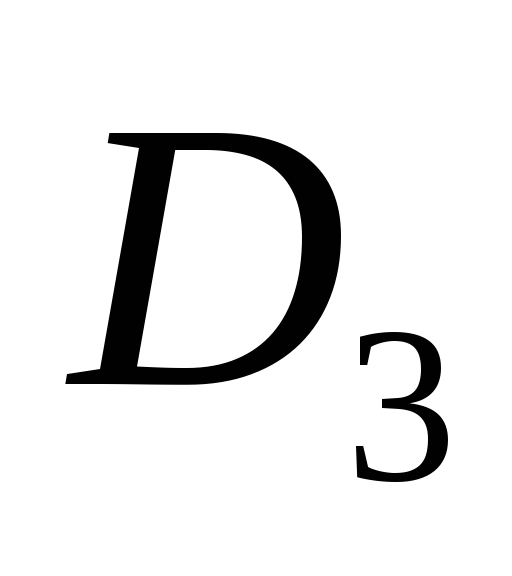 ,
когда салон обслуживают три мастера,
и определить, выгодно ли принять на
работу третьего мастера с точки зрения
общего дохода, полученного за 1 час
работы салона.
,
когда салон обслуживают три мастера,
и определить, выгодно ли принять на
работу третьего мастера с точки зрения
общего дохода, полученного за 1 час
работы салона.
