
- •Сборник заданий по математике
- •Содержание Требования к оформлению контрольных работ ...................................... 2
- •Раздел 1. Линейная алгебра .................….............................................. 3
- •Список учебной литературы ...................................................................... 24 Требования к оформлению контрольных работ
- •Формирование исходных данных к задачам
- •1. Линейная алгебра
- •2. Аналитическая геометрия
- •3. Дифференциальное исчисление.
- •Интегральное исчисление.
- •Функции нескольких переменных.
- •Двойные, тройные и криволинейные интегралы.
- •Элементы теории поля.
- •Дифференциальные уравнения.
- •Функции комплексного переменного.
- •Операционное исчисление.
- •Теория вероятностей.
- •Случайные величины.
- •Элементы математической статистики
- •Линейное программирование.
- •Задача оптимального производства продукции.
- •Транспортная задача.
- •Матричные игры.
- •Математические методы в экономике.
- •Сетевое планирование.
- •Системы массового обслуживания (смо).
- •Задача межотраслевого баланса.
- •Дискретная математика.
- •Двоичная система счисления.
- •Логика высказываний.
- •Краткое содержание (программа) курса
- •I. Линейная алгебра.
- •2. Аналитичеcкая геометрия.
- •3. Дифференциальное исчисление.
- •4. Интегральное исчисление.
- •5. Функции нескольких переменных.
- •6. Двойные, тройные и криволинейные интегралы.
- •7. Элементы теории поля.
- •Список учебной литературы
3. Дифференциальное исчисление.
-
Пределы, непрерывность и разрывы функций.
-
Найти пределы функций:
-
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
-
В точках
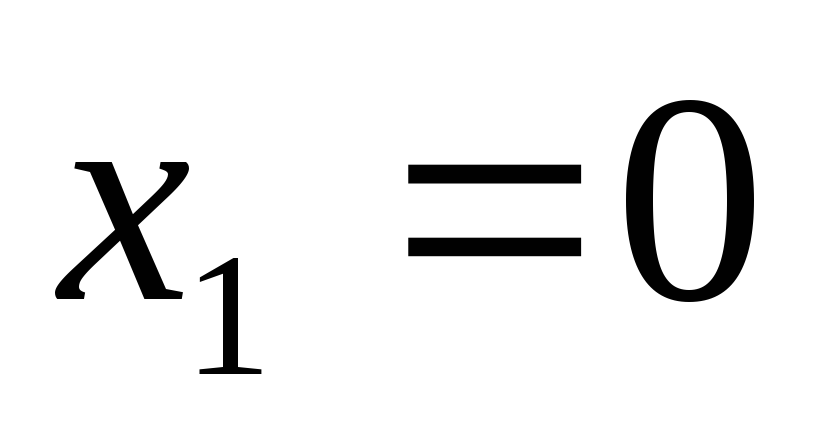 и
и
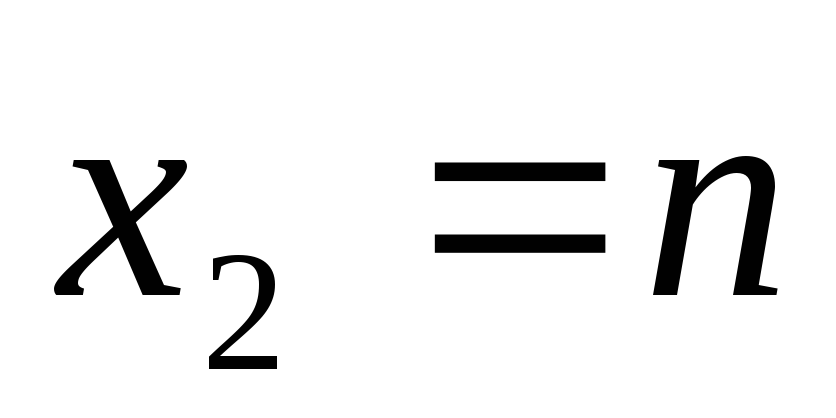 для функции
для функции
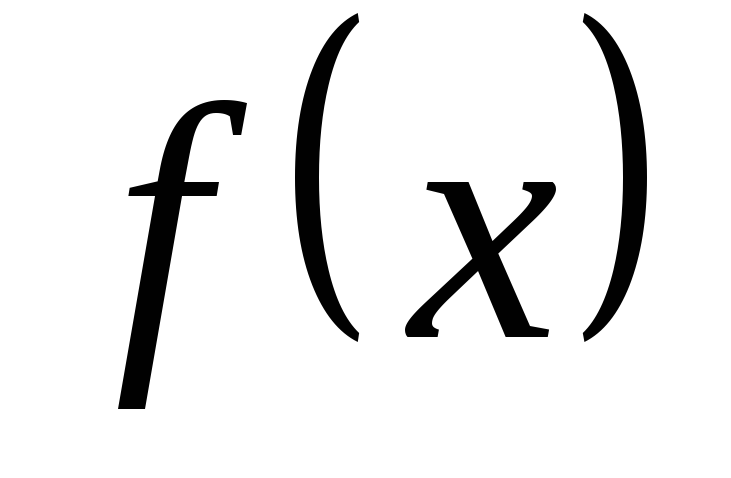 установить непрерывность или определить
характер точек разрыва. Нарисовать
график функции
установить непрерывность или определить
характер точек разрыва. Нарисовать
график функции
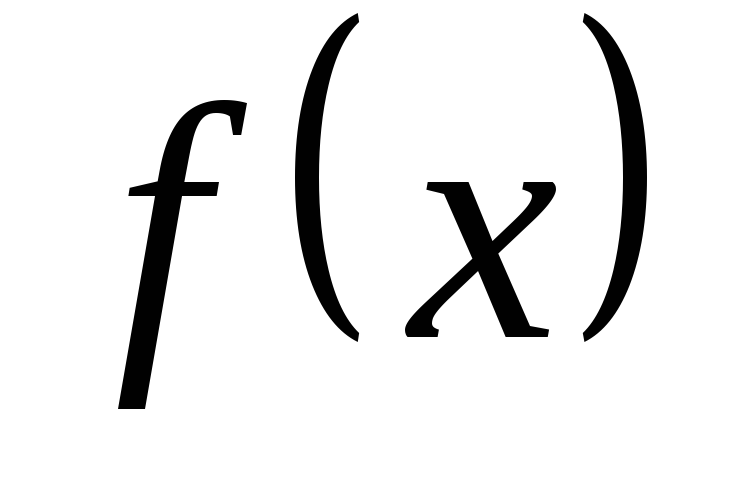 в окрестностях этих точек:
в окрестностях этих точек:
![]() ;
;
-
Производные функций.
-
Найти производные
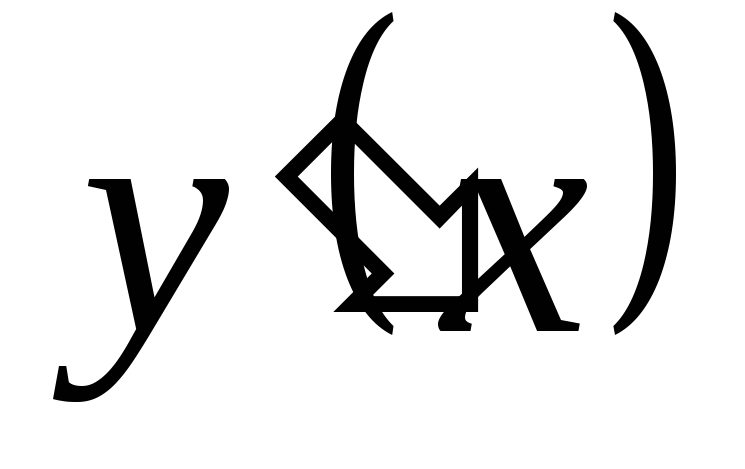 функций:
функций:
-
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
д)
;
д)
![]() ; е)
; е)
![]() ;
;
ж)
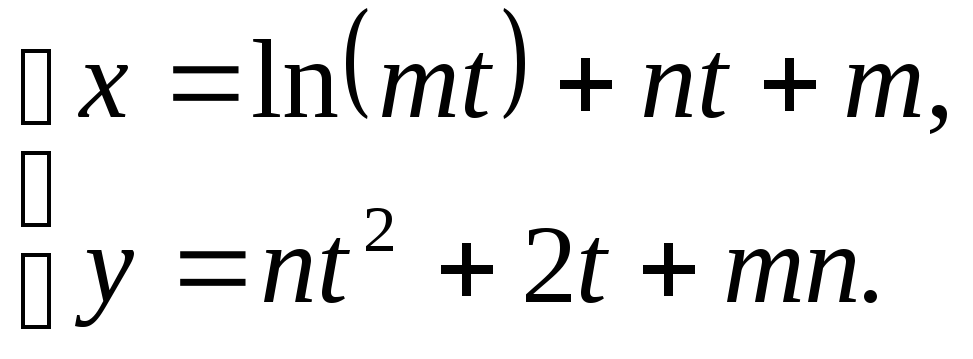
-
Приложения производной.
-
С помощью методов дифференциального исчисления построить график функции
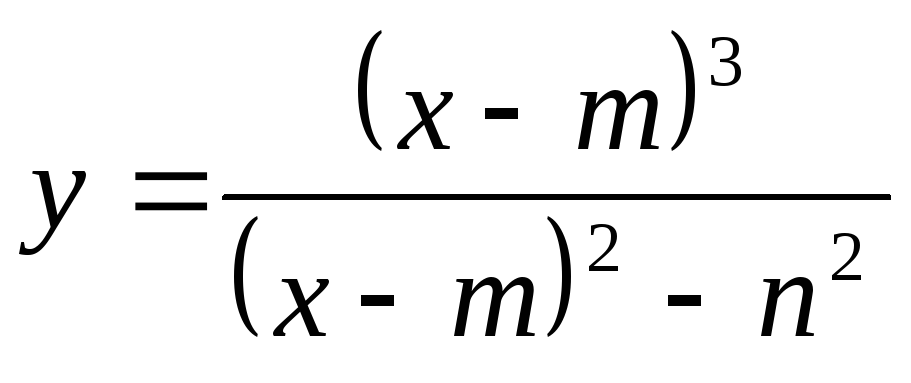 .
.
-
-
Приближенное решение алгебраических уравнений.
-
Для уравнения
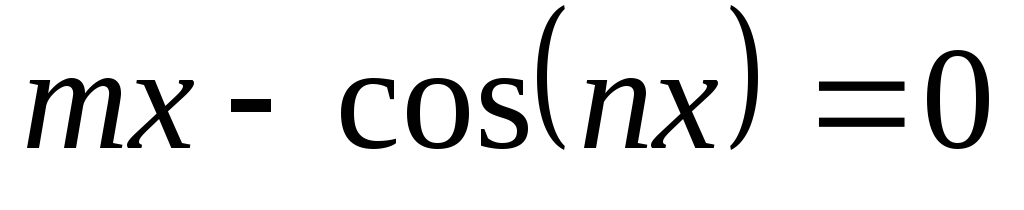 отделить положительный корень и найти
его приближенно с точностью
отделить положительный корень и найти
его приближенно с точностью
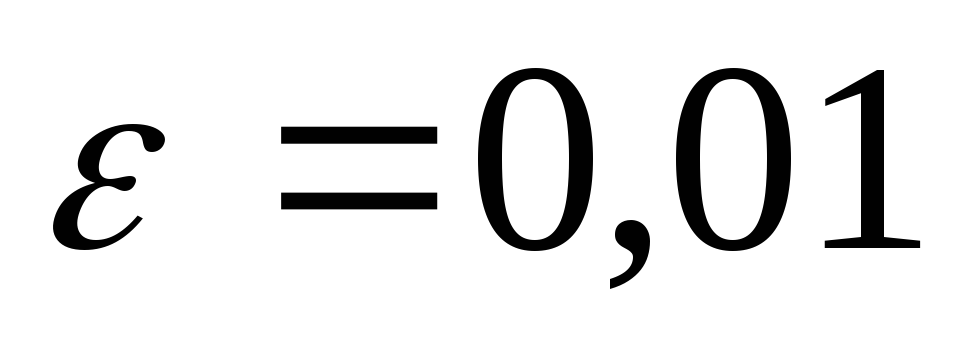 :
:
-
а) методом деления отрезка пополам;
б) методом касательных.
Примечание.
Можно считать, что точность
![]() достигнута, если разность между соседними
приближениями
достигнута, если разность между соседними
приближениями
![]() и
и
![]() удовлетворяет неравенству
удовлетворяет неравенству
![]() .
.
-
Интегральное исчисление.
-
Неопределенный интеграл.
-
Найти интегралы:
-
а)
![]() ; б)
; б)
![]() ;
д)
;
д)
![]() .
.
-
Несобственные интегралы.
-
Вычислить интеграл или установить его расходимость:
-
![]()
-
Применения определенных интегралов.
-
Построить схематический чертеж и найти площадь фигуры, ограниченной линиями:
-
![]() ;
;
-
Найти объем тела, полученного при вращении вокруг оси ОХ фигуры, ограниченной линиями:
![]() .
.
-
Приближенное вычисление определенных интегралов.
-
Для вычисления определенного интеграла
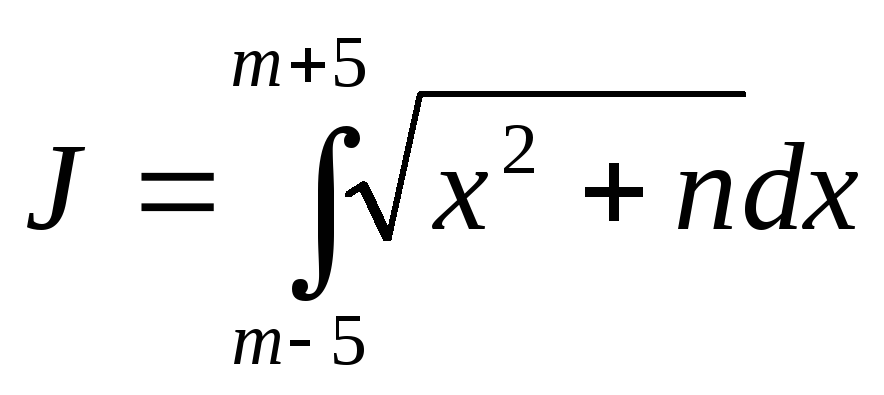 ,
разбивая отрезок интегрирования
сначала на 10 равных частей, а затем на
20 равных частей, найти приближенное
значение
,
разбивая отрезок интегрирования
сначала на 10 равных частей, а затем на
20 равных частей, найти приближенное
значение
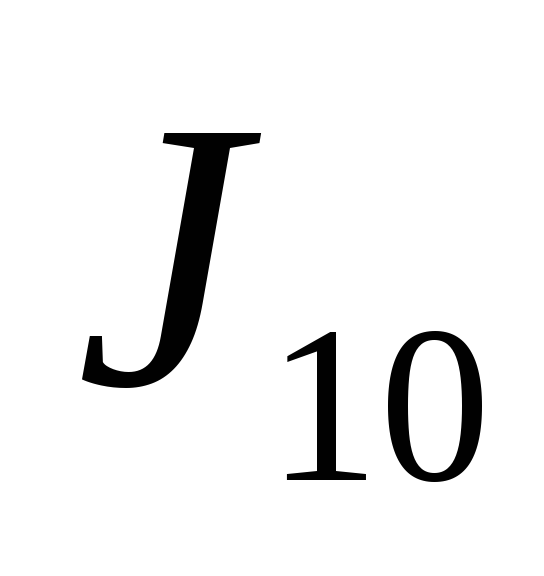 и
и
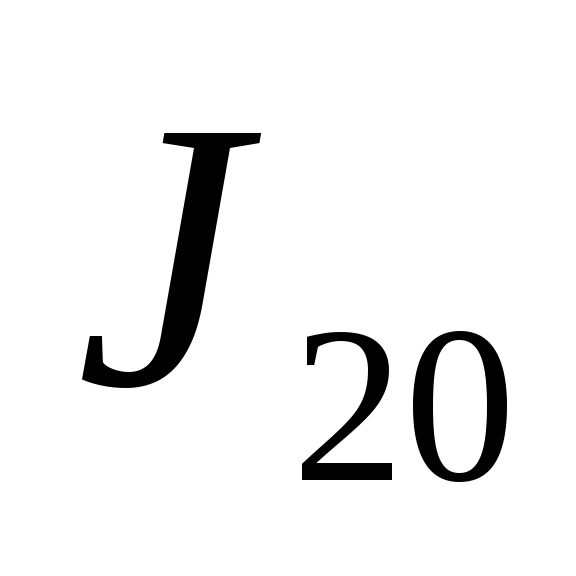 :
а) по формуле трапеций; б) по формуле
Симпсона. Оценить точность приближения
с помощью разности
:
а) по формуле трапеций; б) по формуле
Симпсона. Оценить точность приближения
с помощью разности
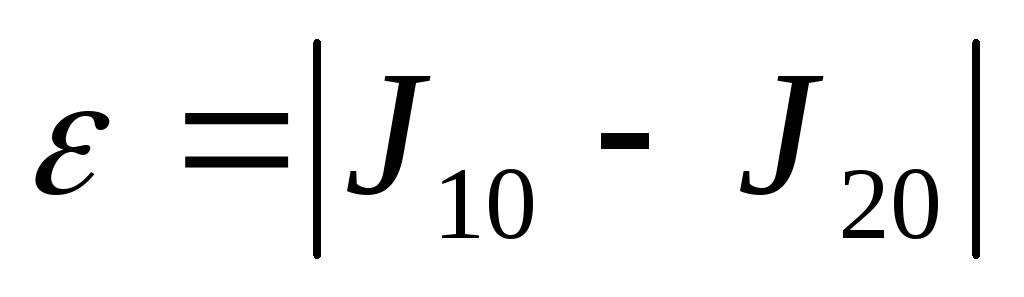 .
.
-
-
Функции нескольких переменных.
-
Частные производные и дифференциал функции.
-
Найти дифференциал
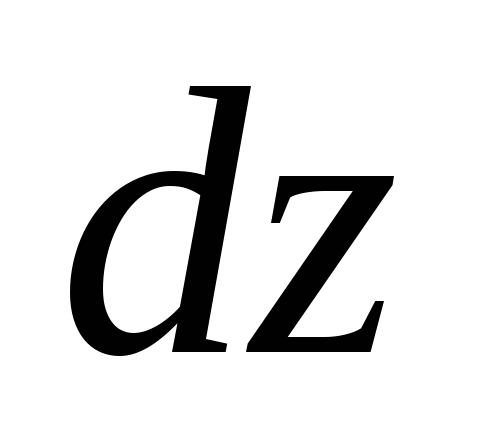 функции
функции
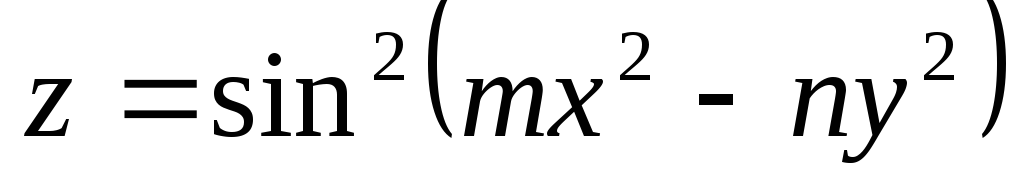 .
. -
Показать, что функция
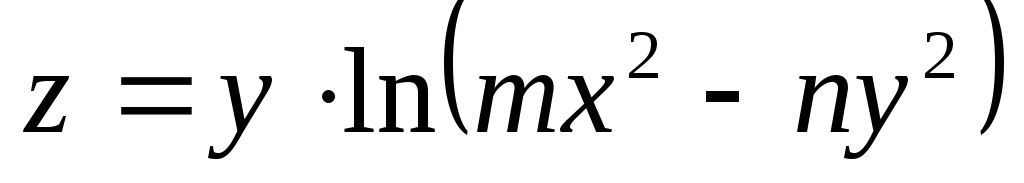 удовлетворяет уравнению
удовлетворяет уравнению
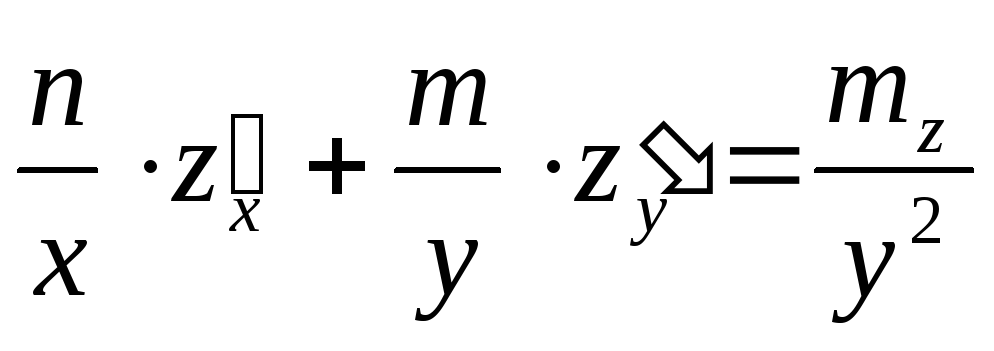 .
.
-
Приложения частных производных.
-
Составить уравнения касательной плоскости и нормали к поверхности
 в точке
в точке
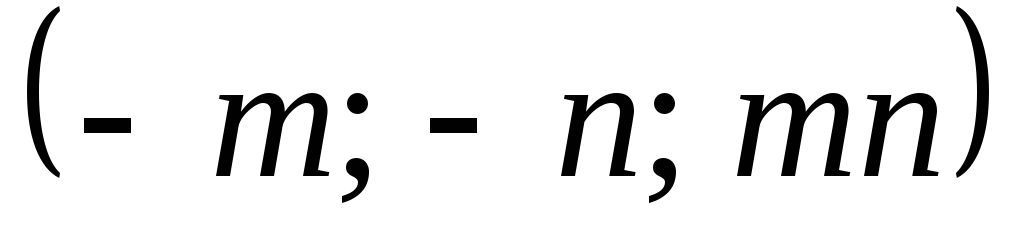 .
. -
Для функции
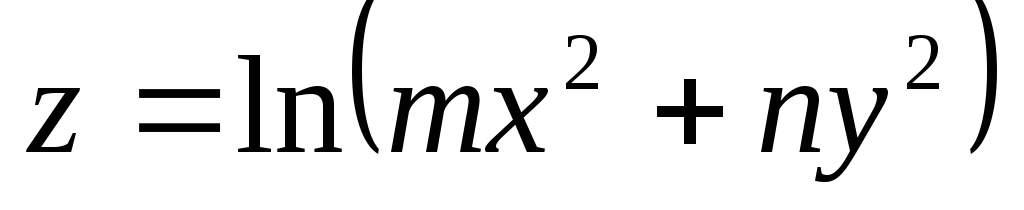 в точке
в точке
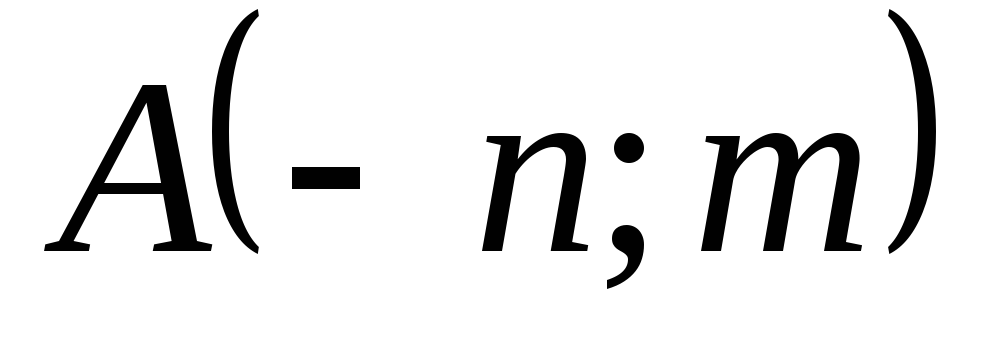 найти градиент и производную по
направлению
найти градиент и производную по
направлению
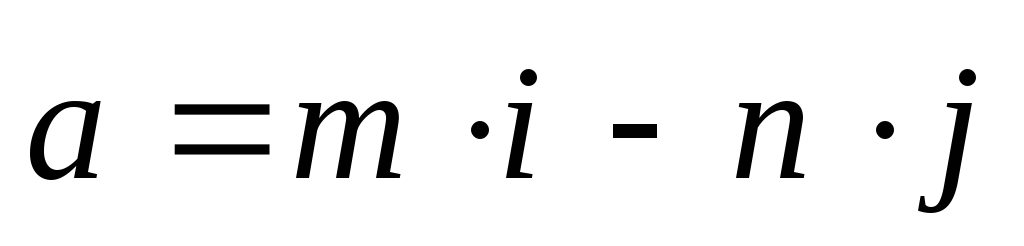 .
.
-
-
Двойные, тройные и криволинейные интегралы.
-
Двойные интегралы.
-
Изменить порядок интегрирования:
-
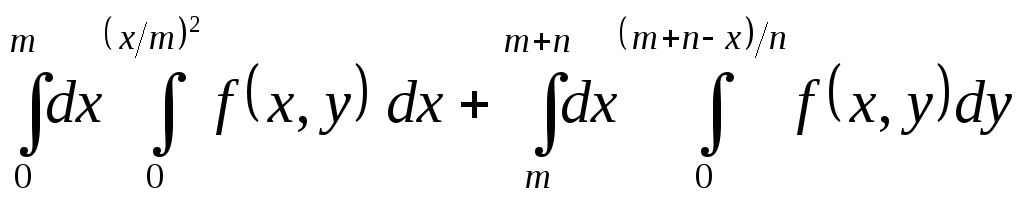 .
.
-
Сделать чертеж и найти объем тела, ограниченного поверхностями
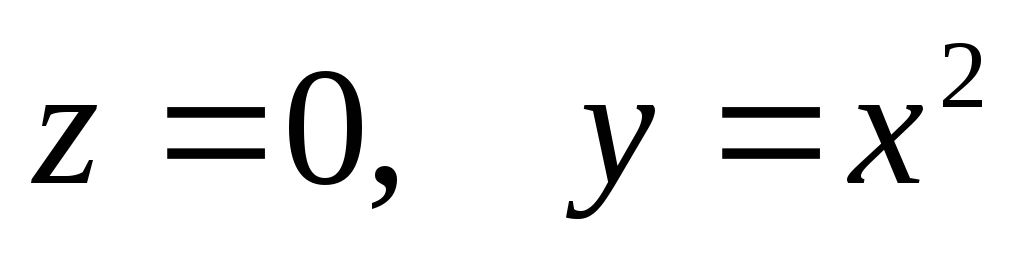 и плоскостью, проходящей через точки
и плоскостью, проходящей через точки
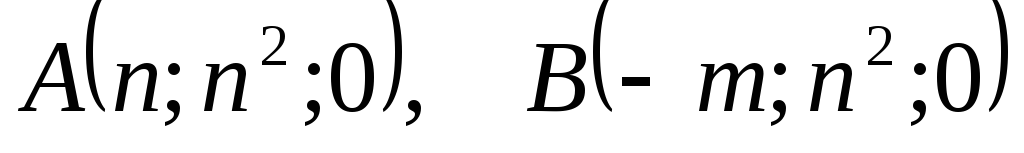 и
и
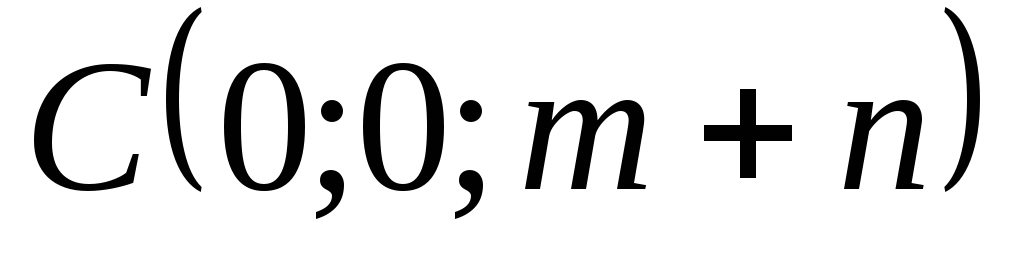 .
. -
Сделать чертеж и найти площадь фигуры, ограниченной линиями:
а)
![]() .
.
-
Тройные интегралы.
-
Найти
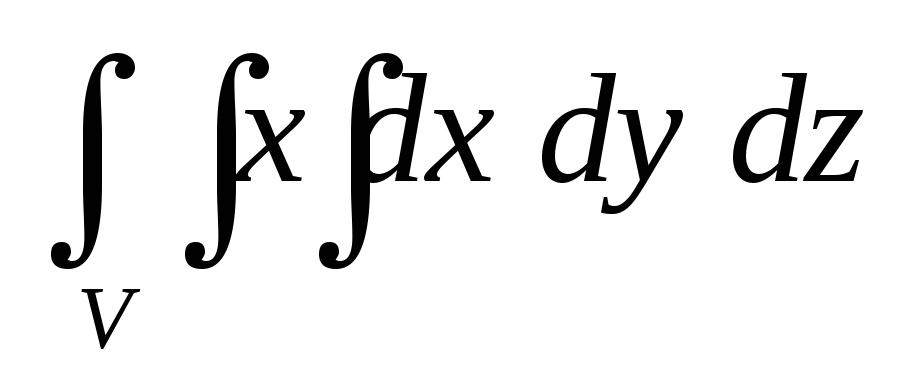 ,
если тело V
ограниченно плоскостями
,
если тело V
ограниченно плоскостями
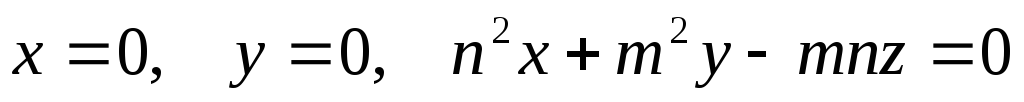 и
и
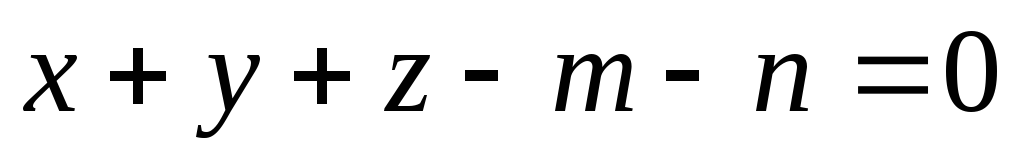 .
. -
Найти объем тела, ограниченного поверхностями
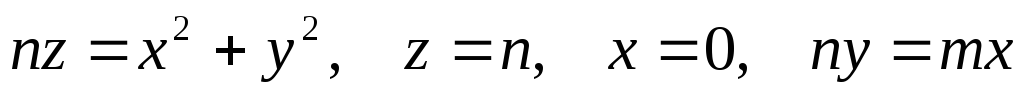 .
.
-
-
Криволинейные интегралы.
-
Вычислить
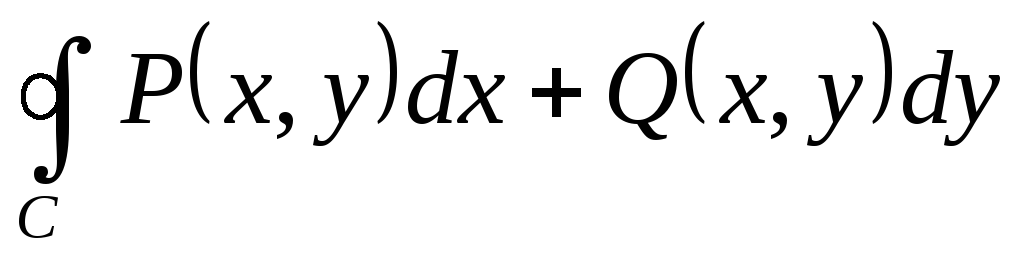 ,
где
,
где
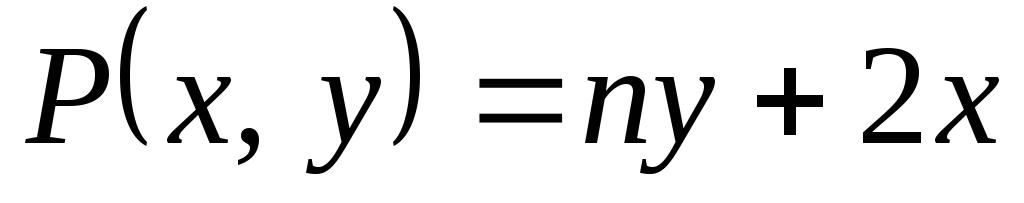 ,
,
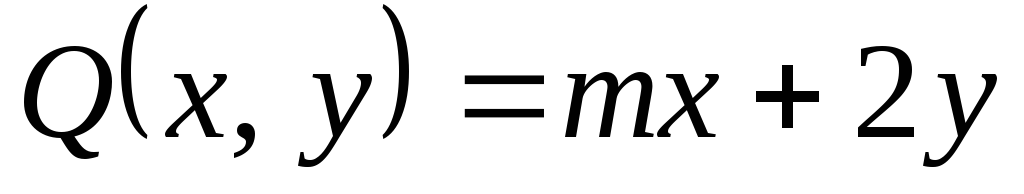 ,
а контур С
образован линиями
,
а контур С
образован линиями
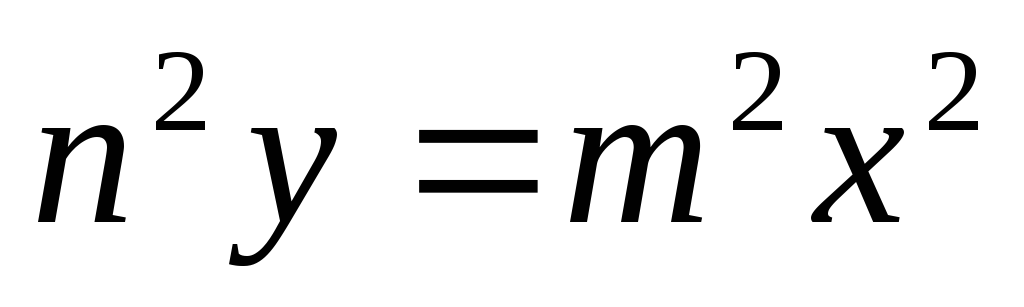 ,
,
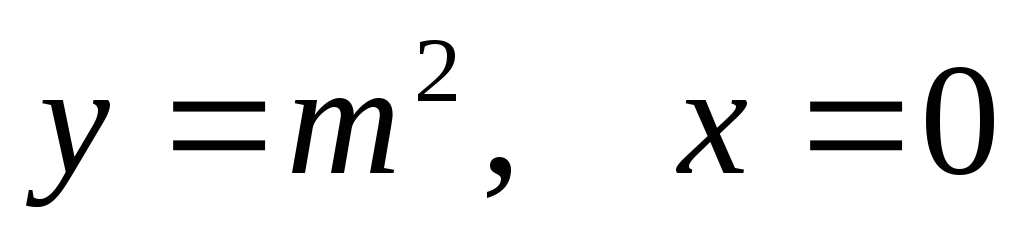 :
а) непосредственно; б) по формуле
Грина.
:
а) непосредственно; б) по формуле
Грина. -
Вычислить
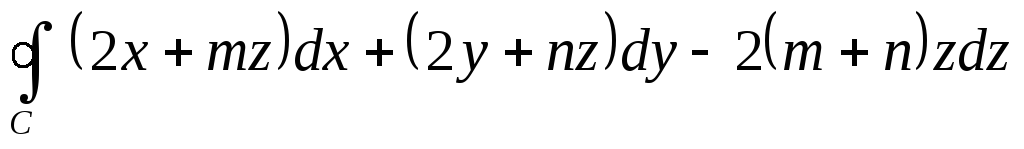 ,
где контур С
является одним витком винтовой линии:
,
где контур С
является одним витком винтовой линии:
-
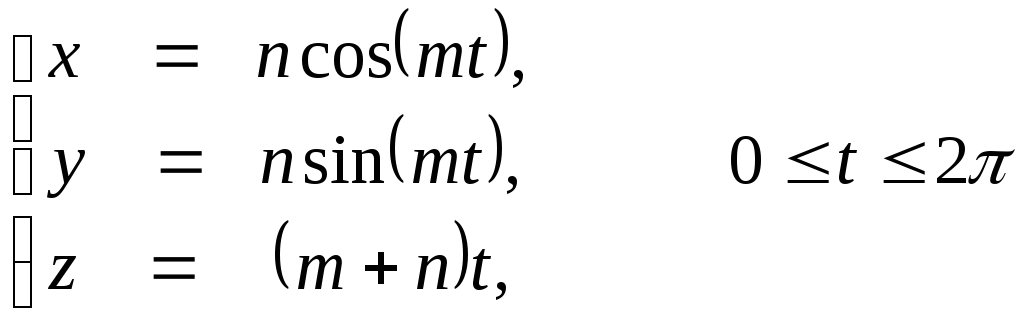 .
.
