3 Построение графика функций двух переменных

Задание 7.

Построить диаграмму типа «Поверхность» для функции при значениях x = [-1;1] и y = [-1;1] с шагом h = 0,1 изменения значений параметров х и у.

Руководство к выполнению Задания 7.

Для программирования начальных данных по каждой переменной х и у необходимо ввести согласно Рисунку 33 их координаты с изменением через шаг h.

При вводе ячейки шага для той и другой переменной необходимо осознавать, что в адресе ячеек необходимо сохранять при копировании формулы – это или столбец, или строка данных. В формулах не задается полностью ссылка на абсолютную ячейку, необходимо закрепить или адрес строки или адрес столбца. Значения х в столбце А и значения у в строке 3 задаем согласно Рисунку 33.

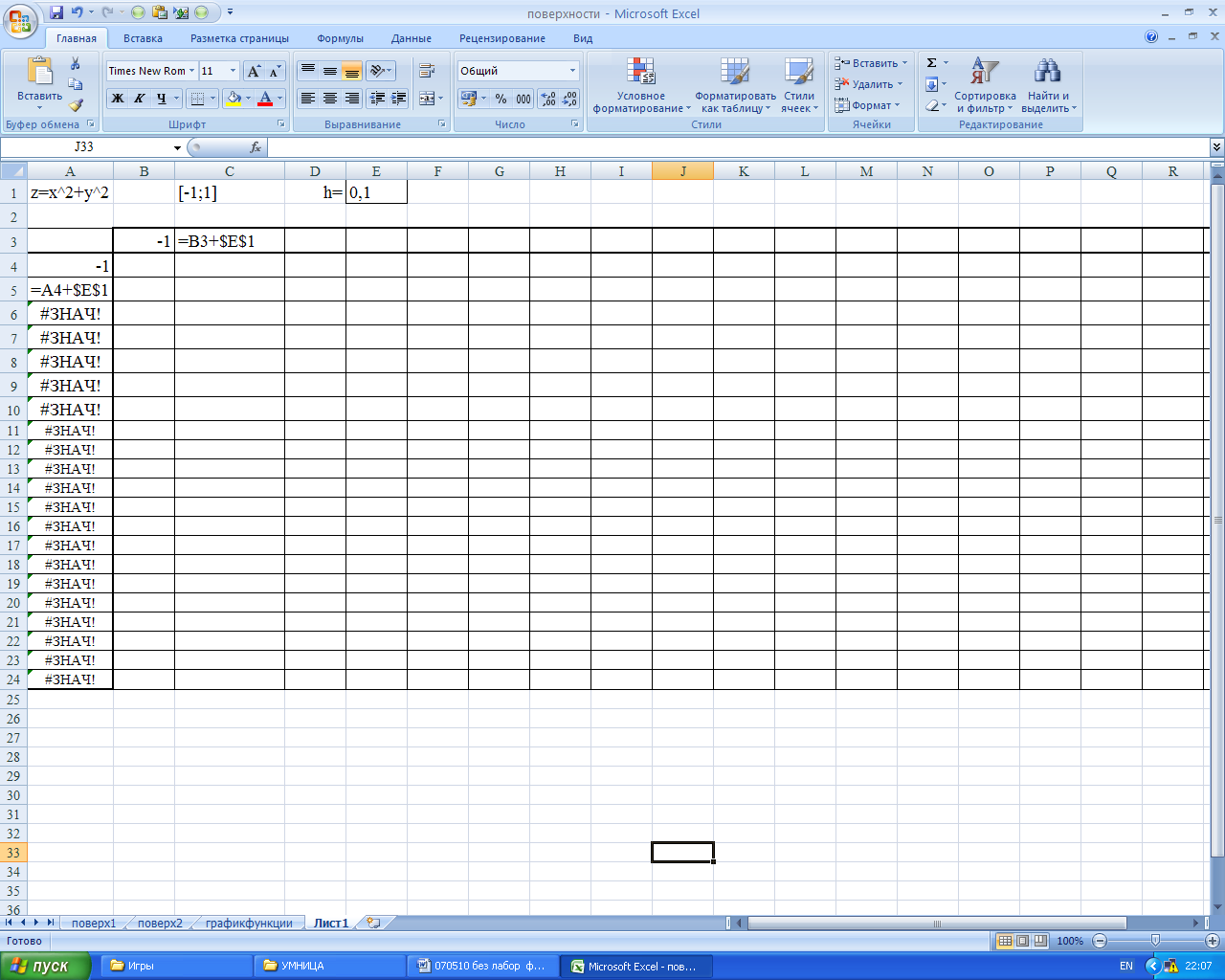
Рисунок 33

Формулу вводим со смешанным закреплением адресов ячеек согласно Рисунку 34.

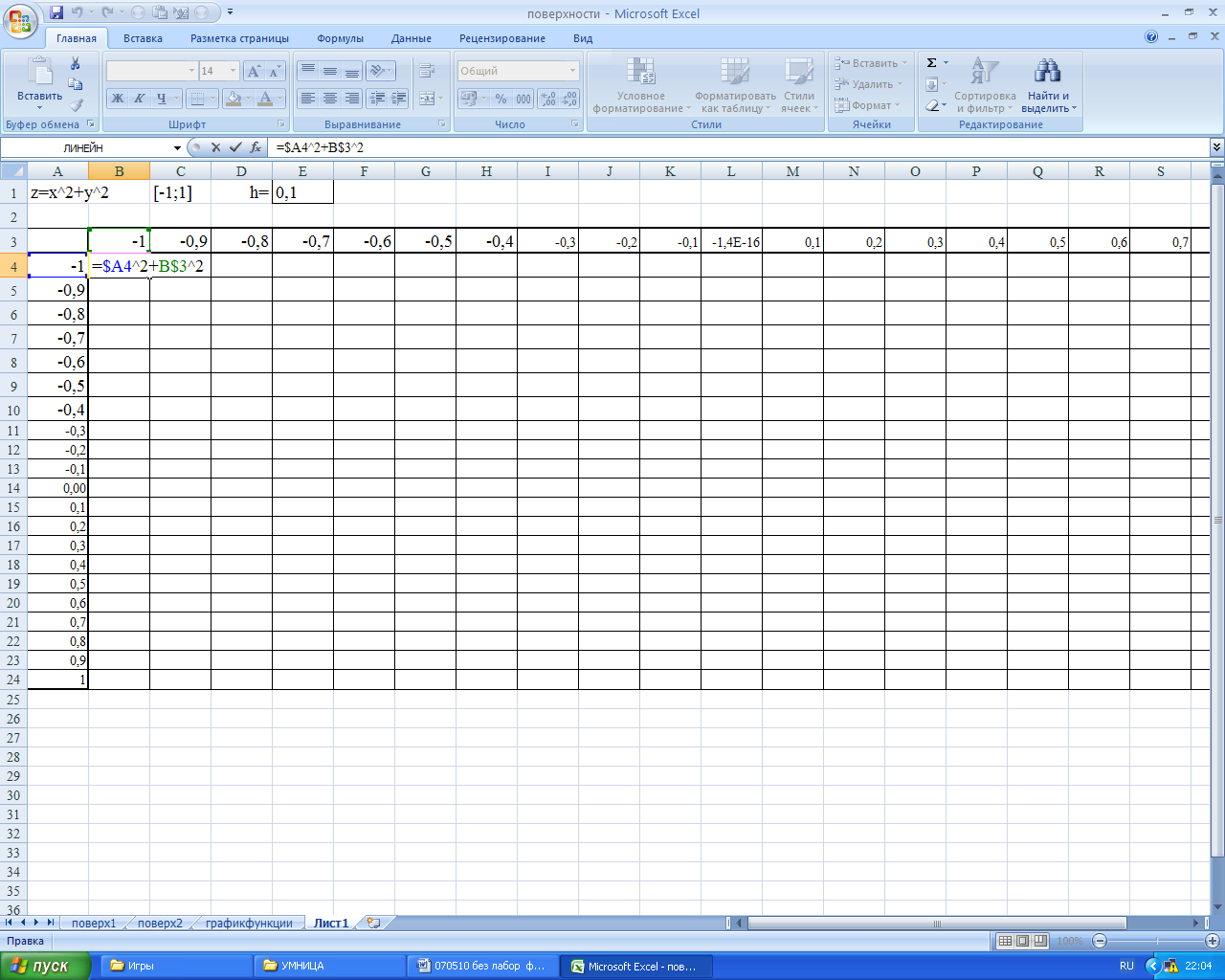
Рисунок 34

При копировании формулы по горизонтали важно следить за изменением адреса строки (т.е. А, В, и т.д.), но при копировании формулы по вертикали, необходимо следить за изменением адреса столбца (т.е. 1, 2,…).

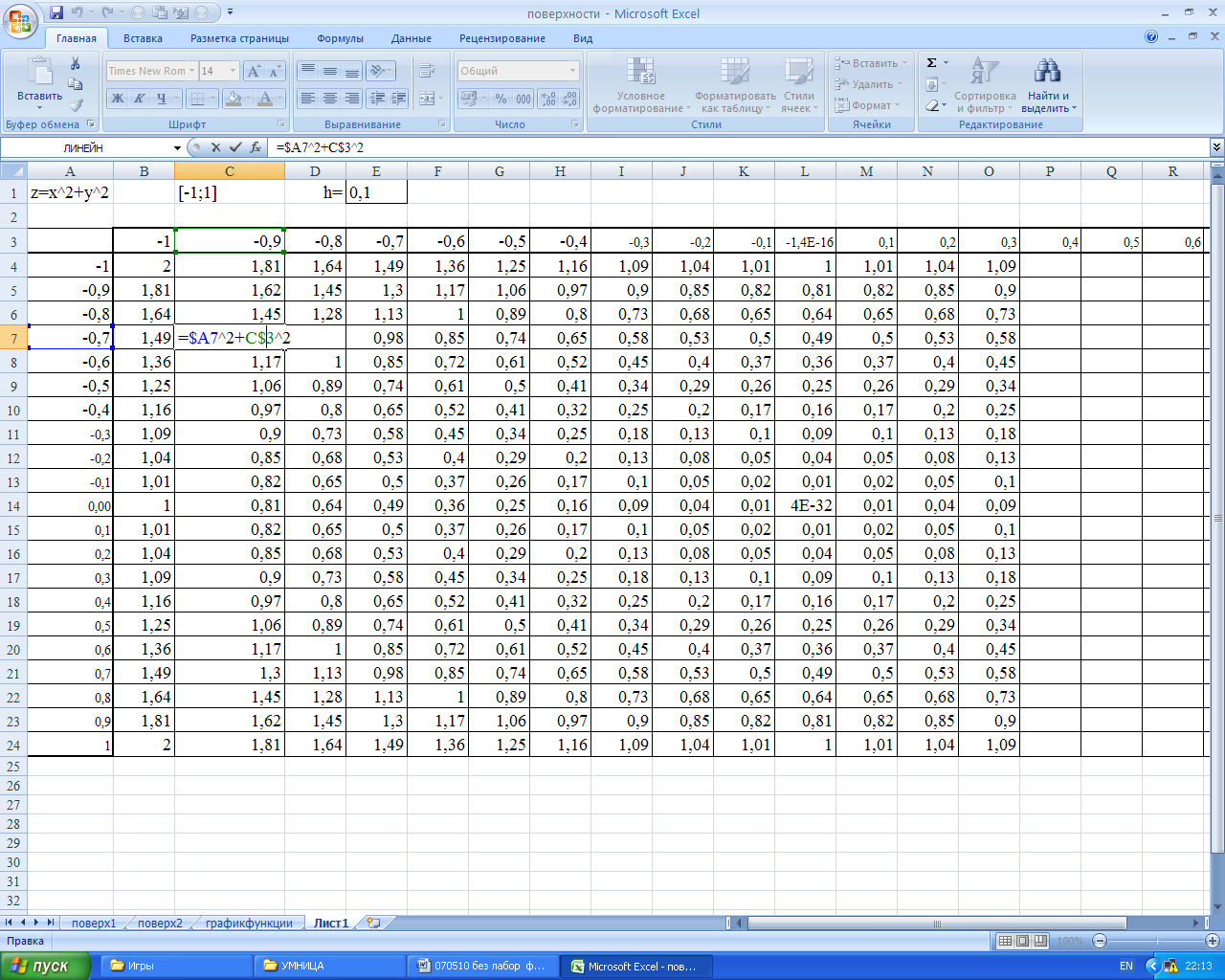
Рисунок 35

При построении диаграммы поверхности необходимо выделять таблицу значений функции, без значений х и у, тип диаграммы построения – «поверхность».

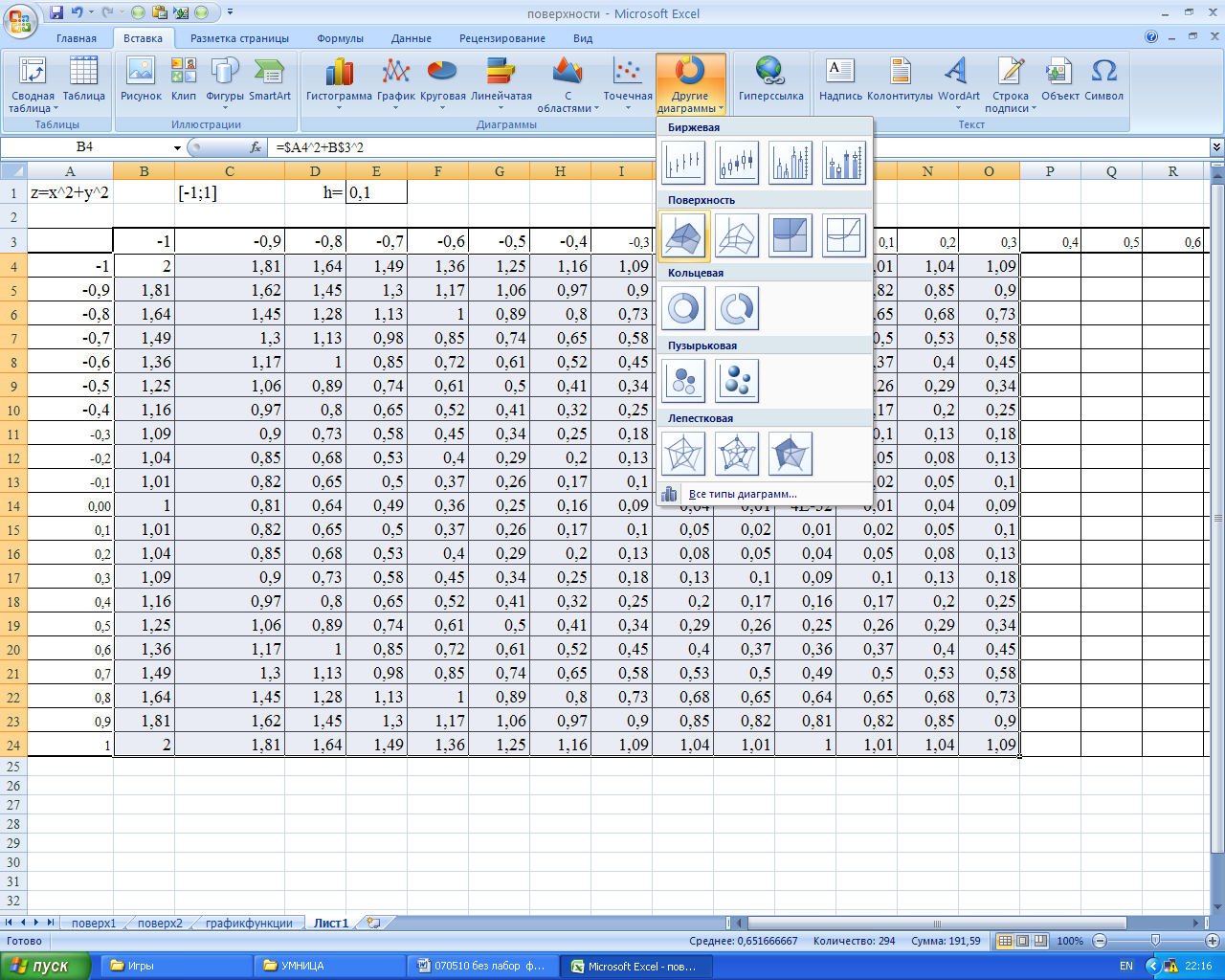
Рисунок 36

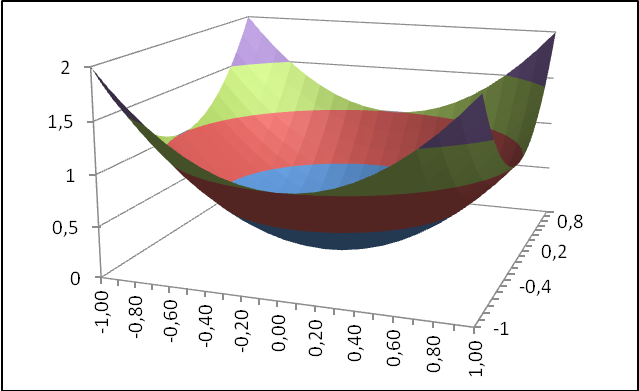
Рисунок 37

Задание 8.

Вычислить значения функции при значениях х = [-1;1] и у = [-1;1] с шагом h = 0,1 изменения значений параметров х и у, построить поверхность z.

Руководство к выполнению Задания 8.

Вычислим значения функции Z при значениях Х = [-1;1] и Y = [-1;1]. На Рисунке 38 показана часть таблицы вычисления функции Z.

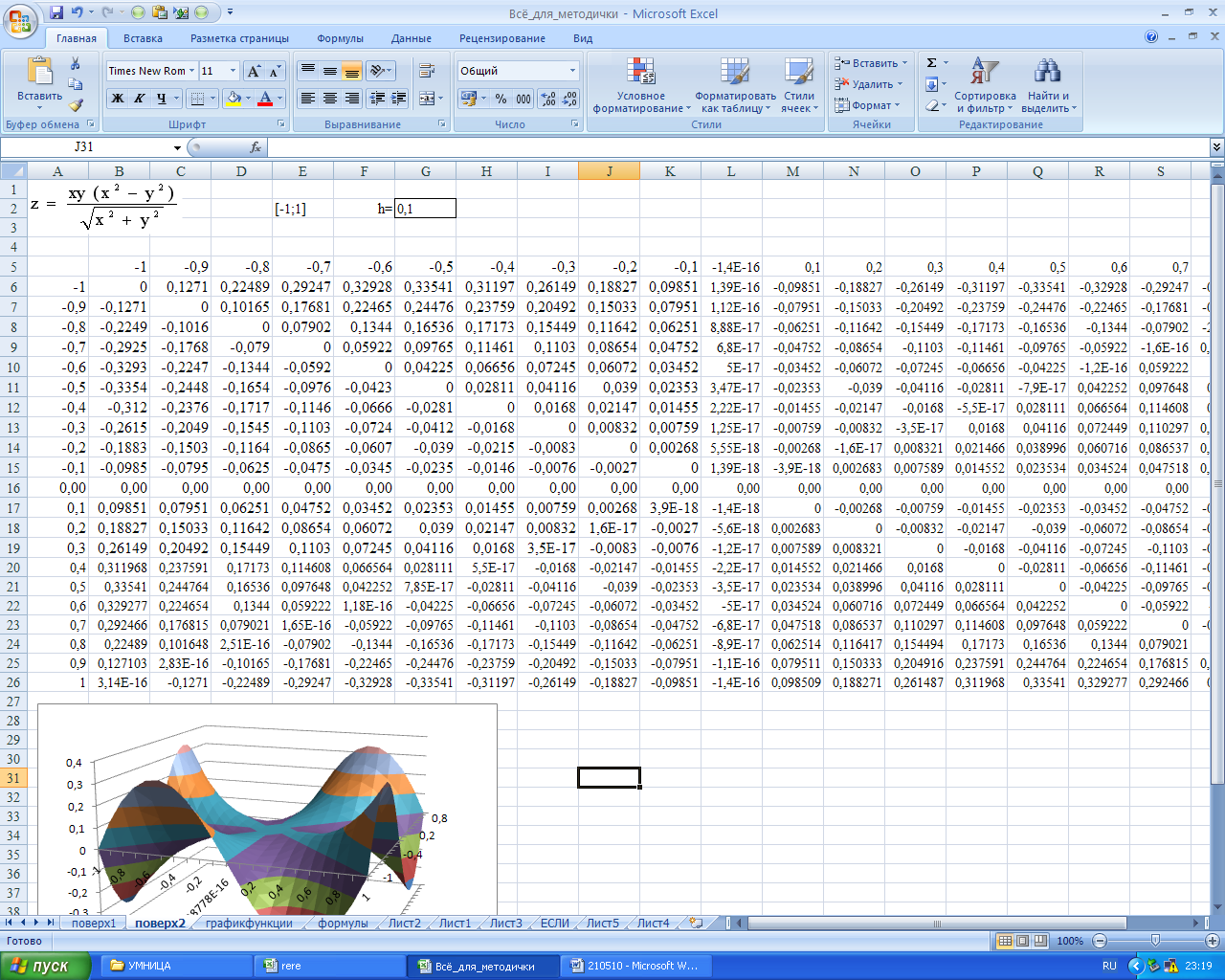
Рисунок 38

В соответствии с Рисунком 39 формулы программы EXCEL вводятся со ссылками на смешанные адреса ячеек.

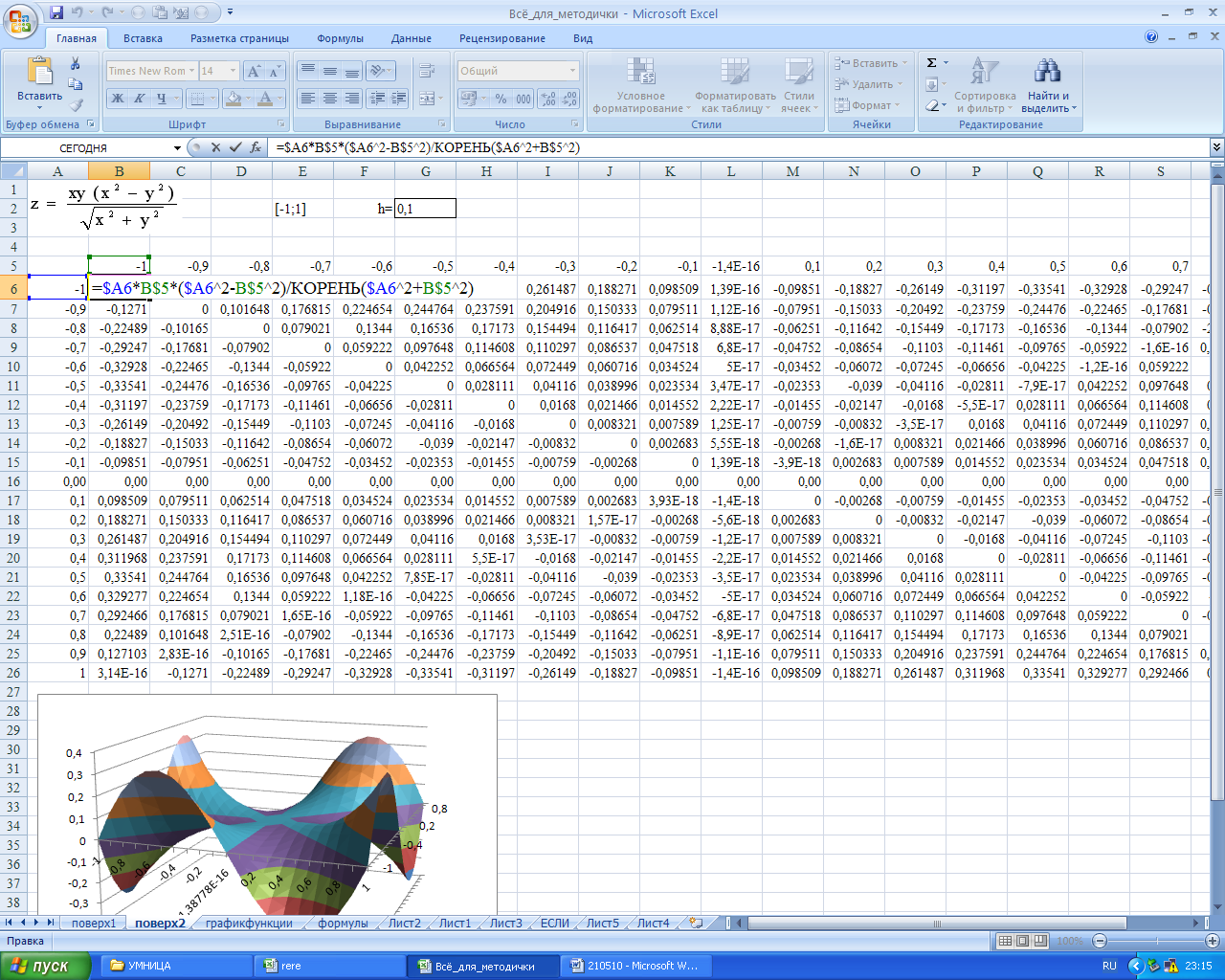
Рисунок 39

Диаграмма вычисленной функции показана на Рисунке 40.

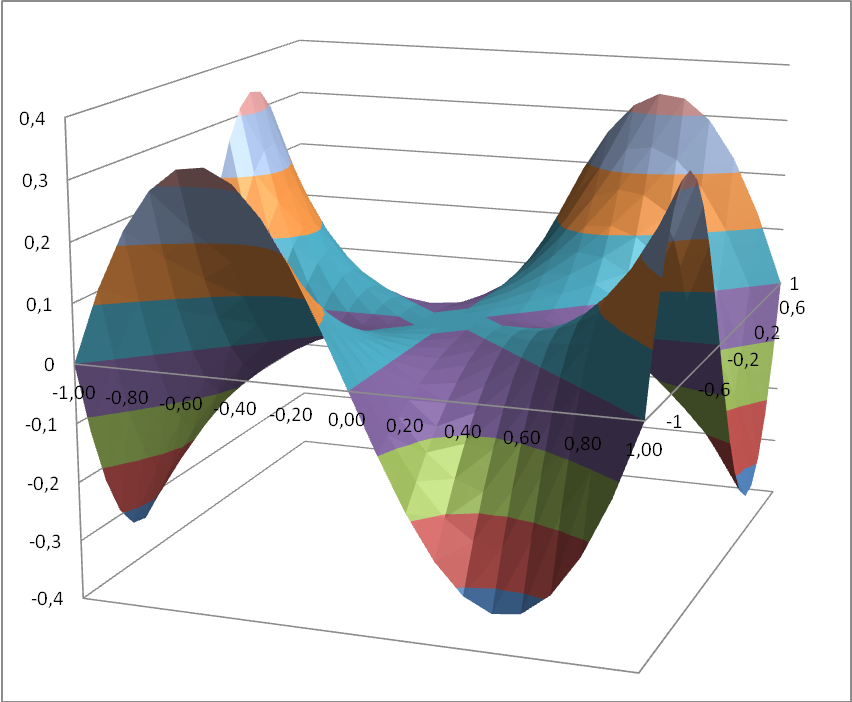
Рисунок 40

4 Решение систем линейных уравнений

Задание 9.

Решить систему линейных уравнений методом Крамера.

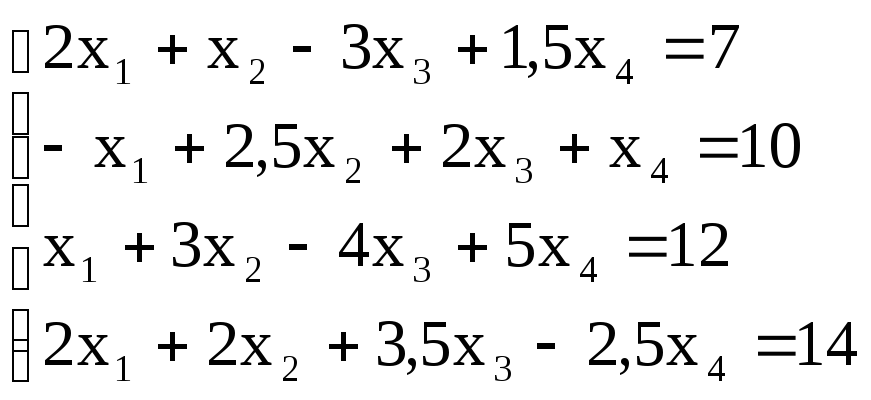
Руководство к выполнению Задания 9.

Для решения системы линейных уравнений в программе EXCEL необходимо ввести в ячейки значений коэффициентов и столбца свободных членов, согласно Рисунку 41 это значения матрицы А и столбца В.

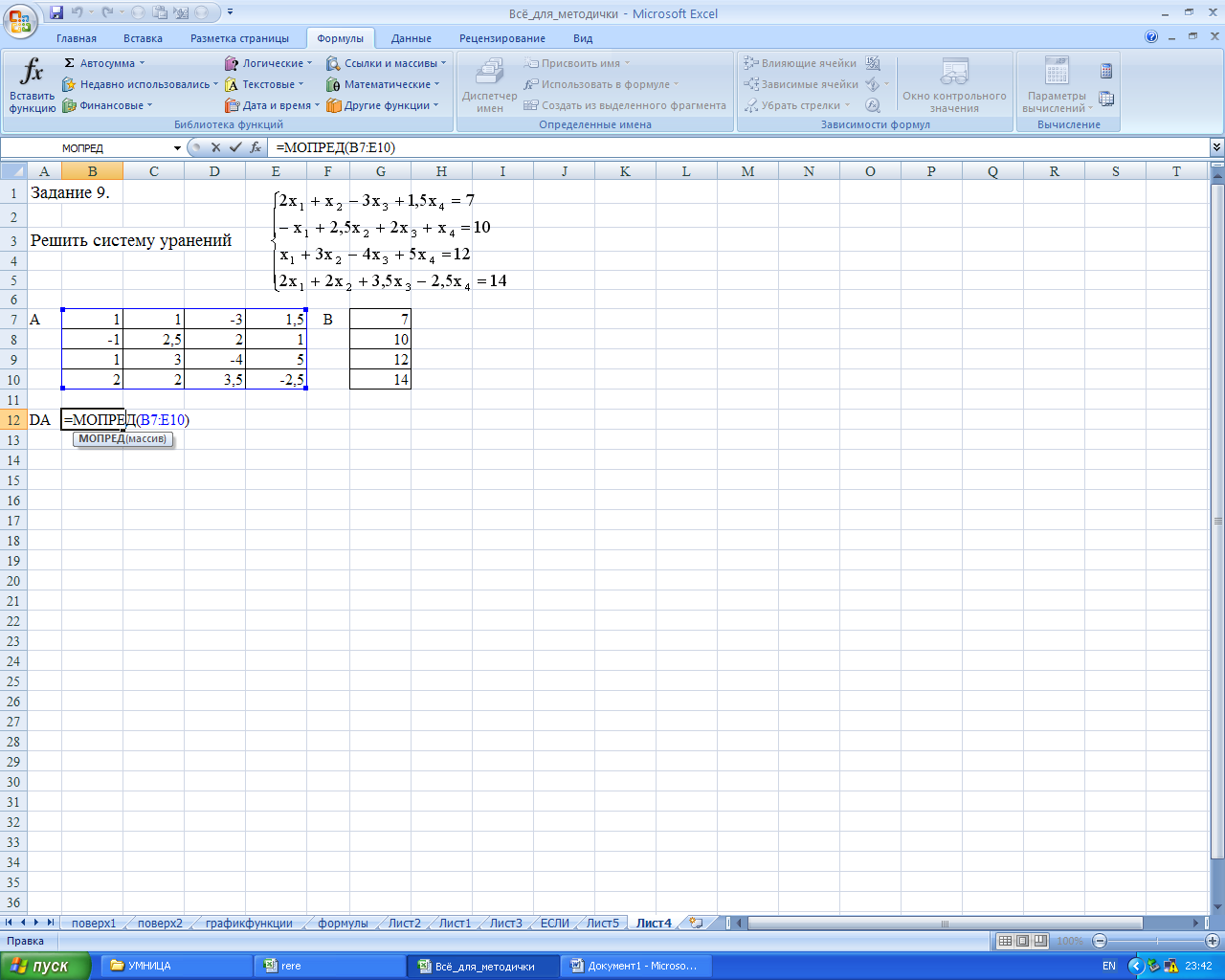
Рисунок 41

В строке формул согласно Рисунку 41 показано, что в ячейке В12 введена формула вычисления значения главного определителя через функцию категории Математические МОПРЕД (массив). При использовании мастера функций в качестве аргумента функции МОПРЕД (массив) выделяются ячейки значений исходной матрицы коэффициентов А.

При вычислении определителей для каждой переменной необходимо копировать ячейки, содержащие запись о матрице А и вычисление её определителя, то есть ячейки А7:Е12 согласно Рисунку 42.

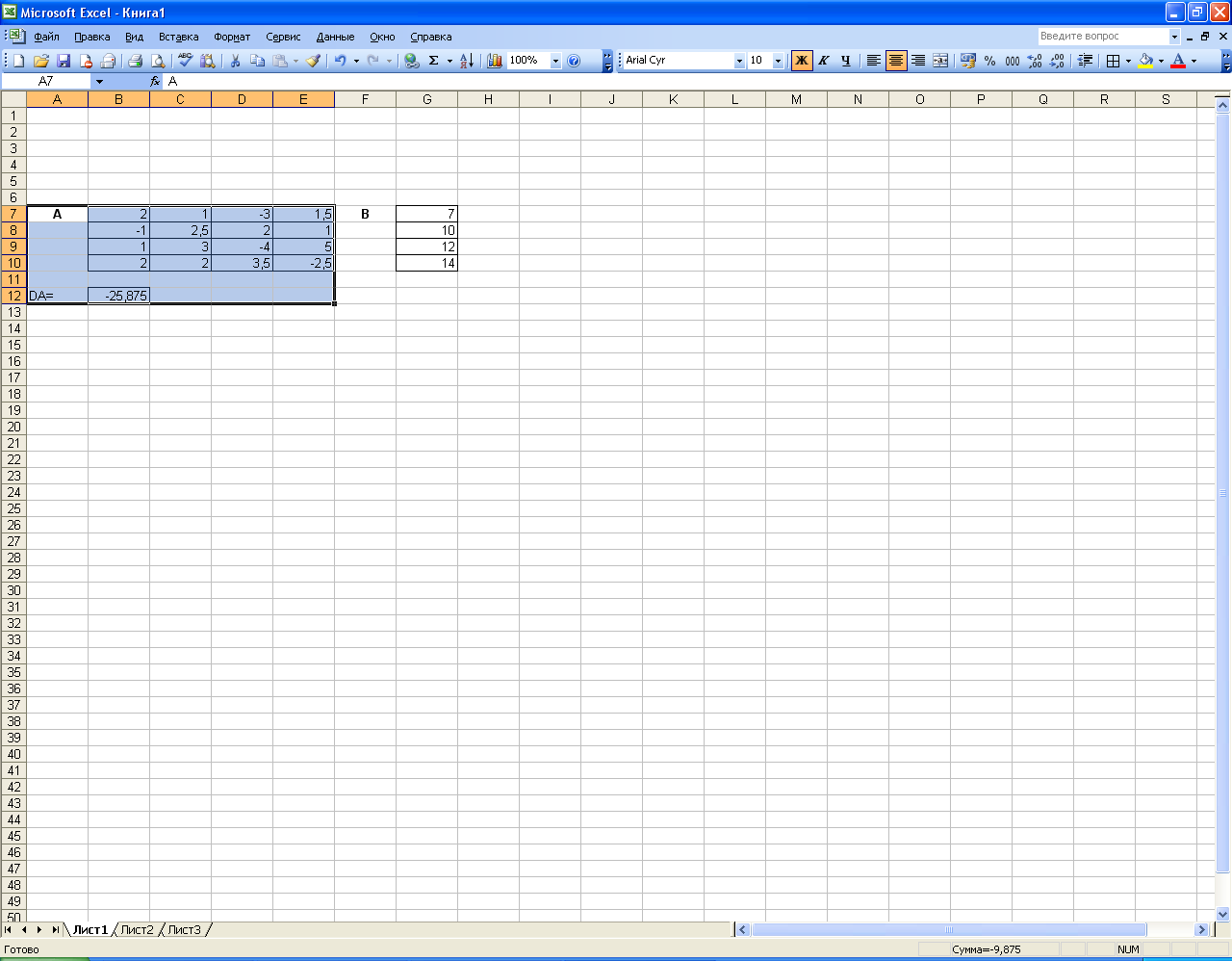
Рисунок 42

Необходимо вставить эту копию ниже 4 раза, так как в системе 4 уравнения и 4 неизвестных.

Для вычисления определителей по каждой переменной надо изменить значения коэффициентов при каждой переменной на значения свободных членов каждого уравнения, для Х1 изменить значения первого столбца, для Х2 – второго и так далее… Это можно сделать копированием и вставкой значений свободных членов в соответствующие столбцы согласно Рисунку 43.

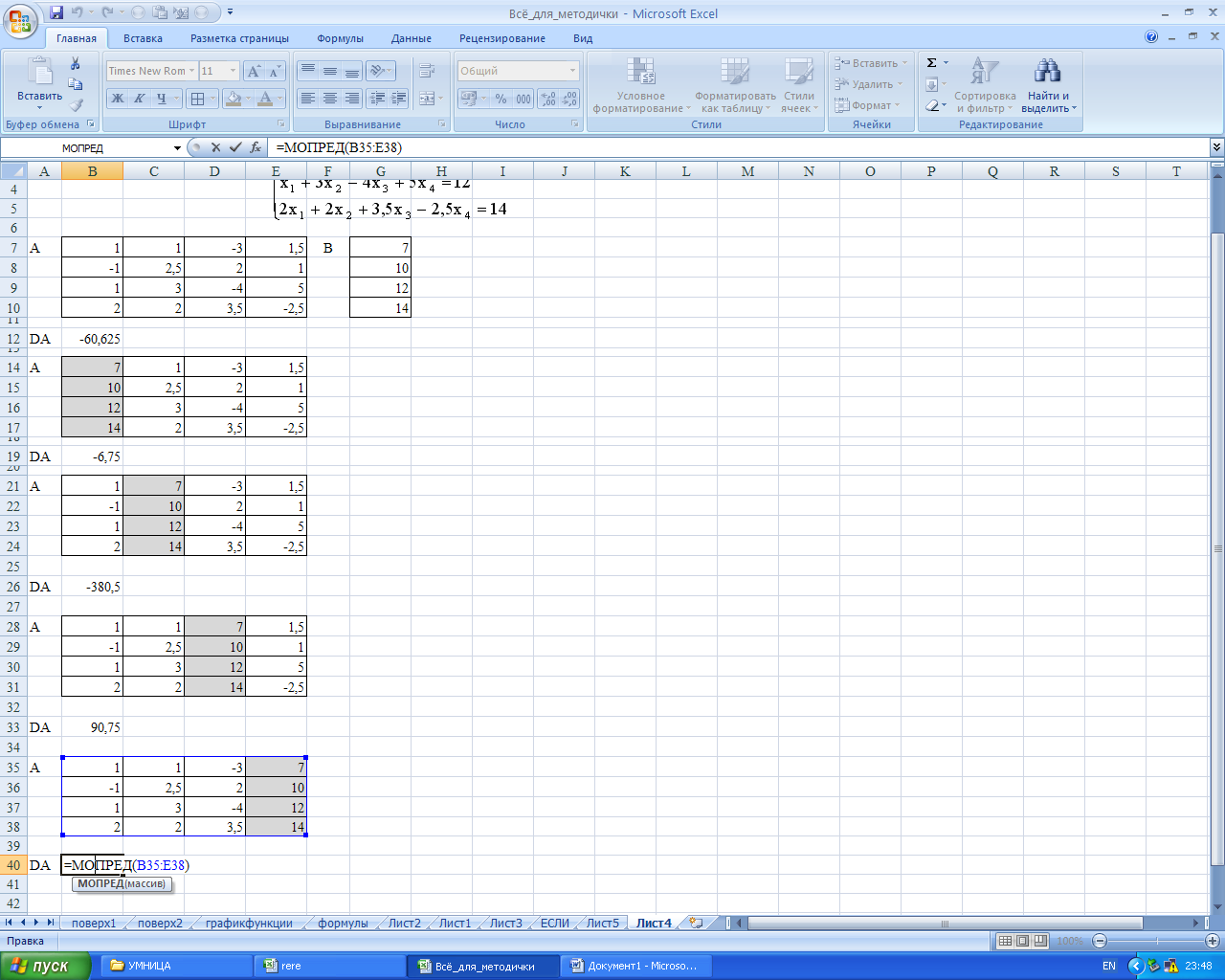
Рисунок 43

Значения определителей вычисляются автоматически.

Значения Х1, Х2, Х3 и Х4 по правилу Крамера определяются по формулам:

_{Вычисление Х1 показано на Рисунке 44.}

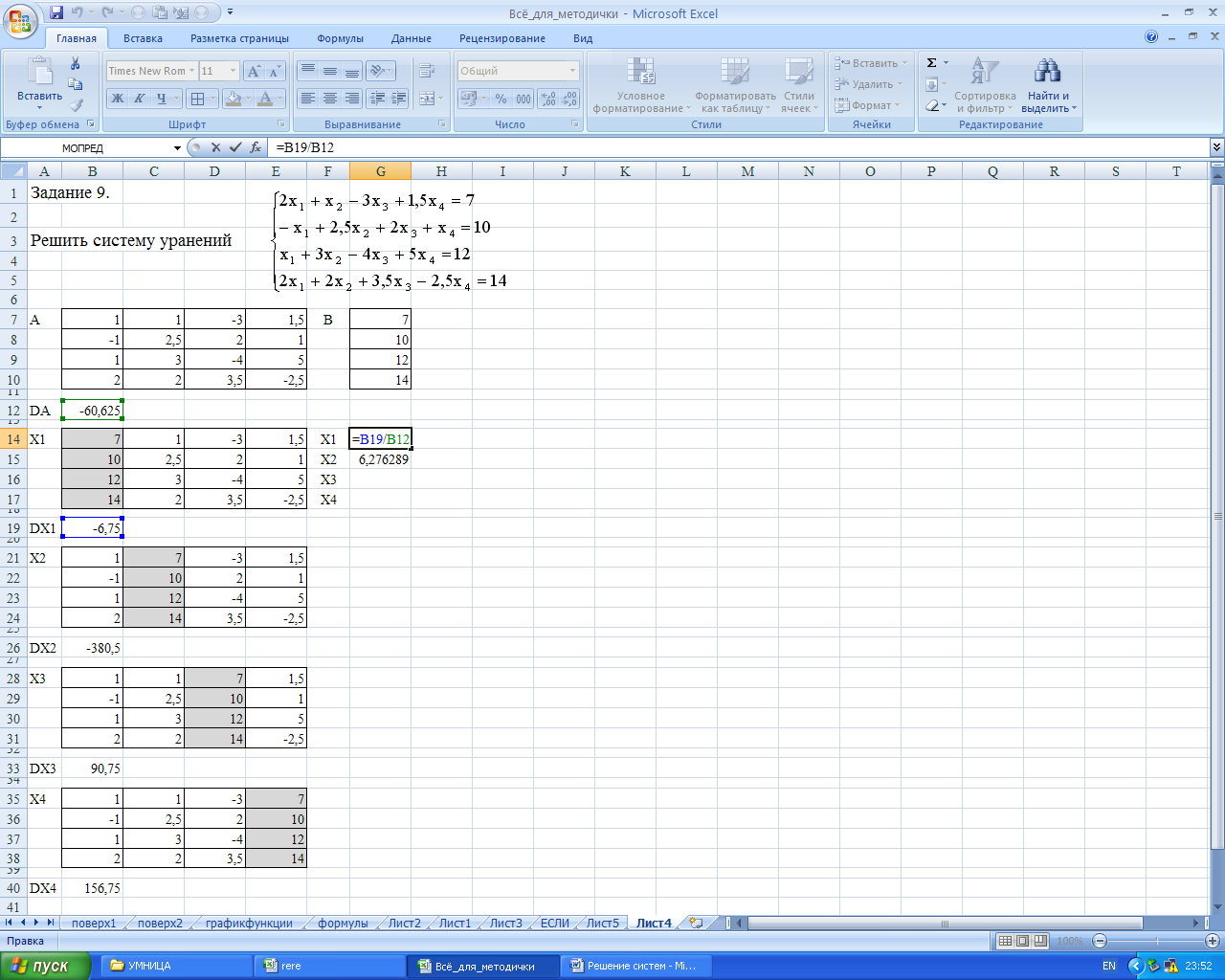
Рисунок 44

Для проведении проверки полученного решения выделяется четыре ячейки одного столбца, используется функция МУМНОЖ (Массив1, Массив2), где согласно Рисунку 45 для Массива1 выделяется исходная матрица коэффициентов А, для Массива2 – столбец найденного решения, результат вводится тремя клавишами Ctrl + Shift + Enter .

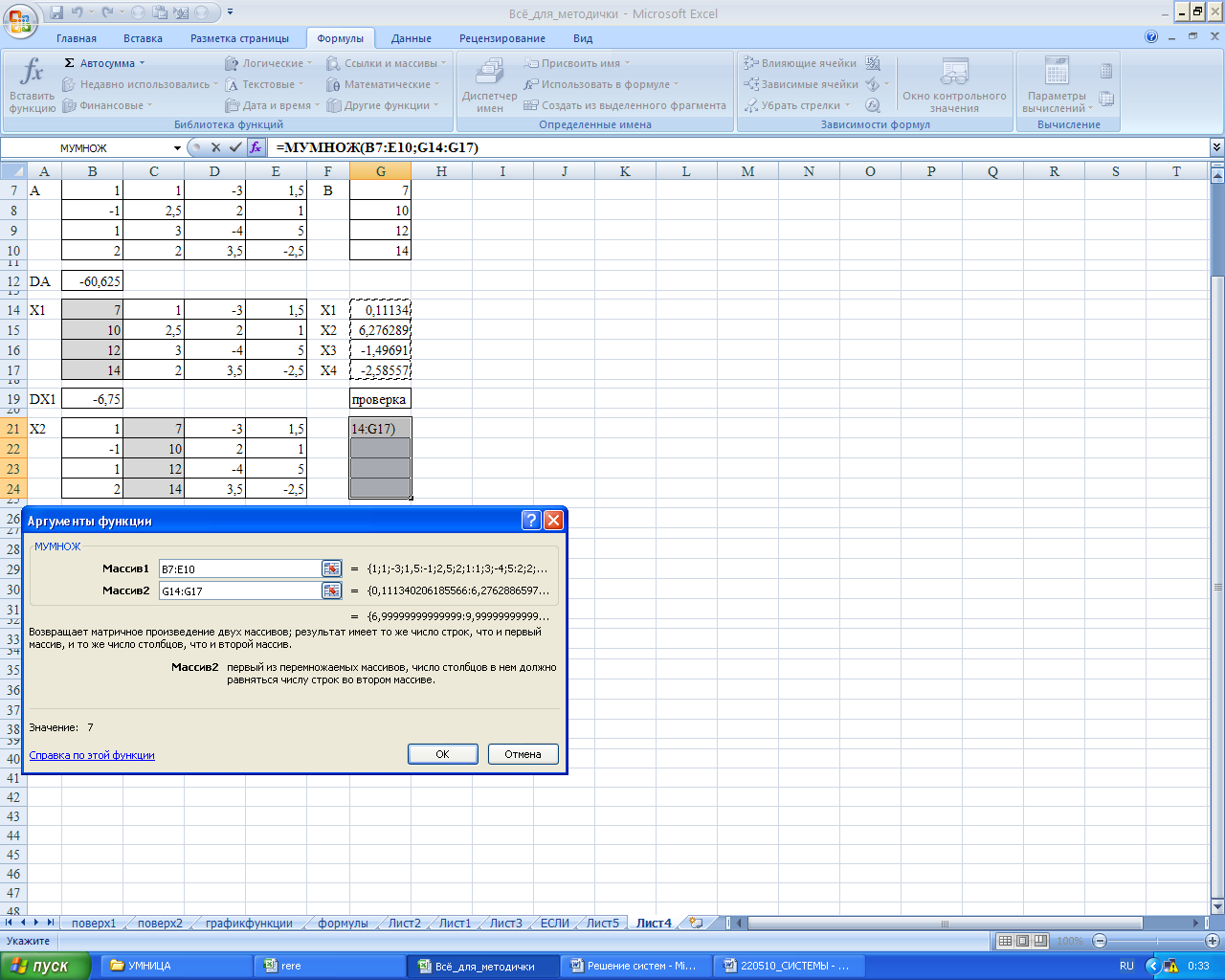
Рисунок 45

Если не получилось четыре значения, необходимо проверить выделение четырех ячеек, поставить курсор в строку формул и повторить нажатие указанных клавиш Ctrl + Shift + Enter согласно Рисунку 46.

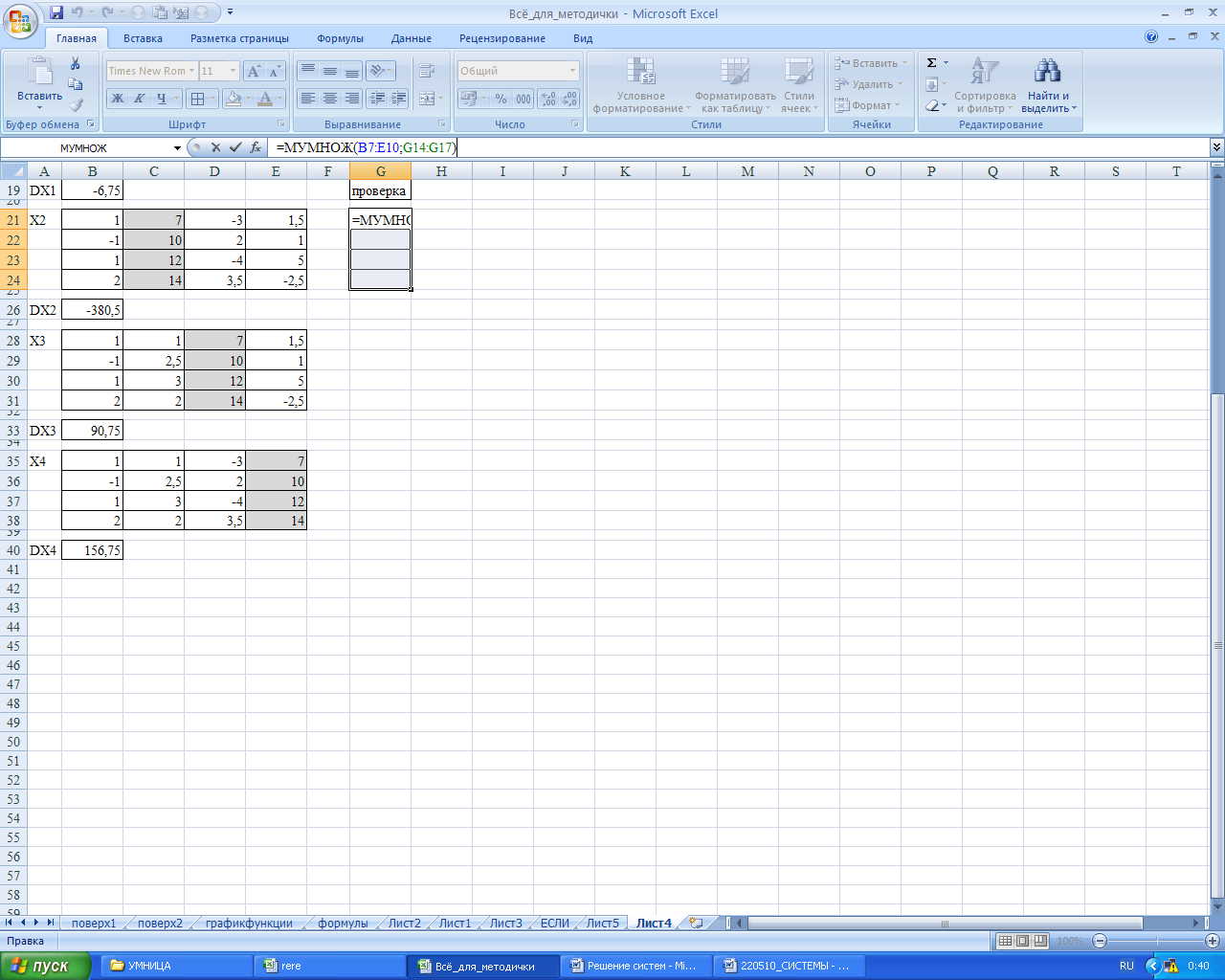
Рисунок 46

При правильно выполнении нажатия трех клавиш формула в Строке формул будет записана в фигурных скобках согласно Рисунку 47.

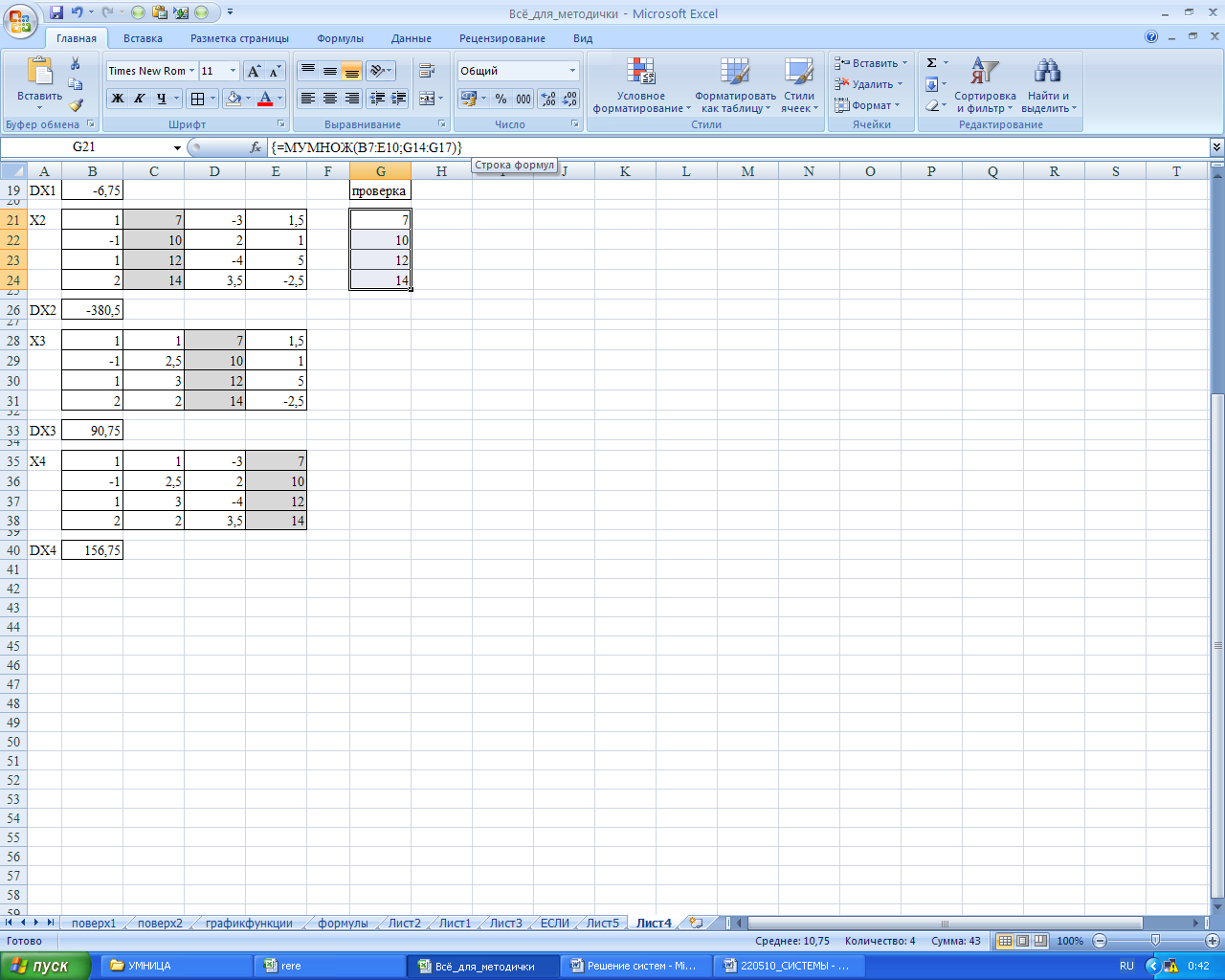
Рисунок 47

Значения, полученные в результате проверки, должны равняться значениям свободных членов заданной системы. Оформление Задания 9 показано на Рисунке 48.

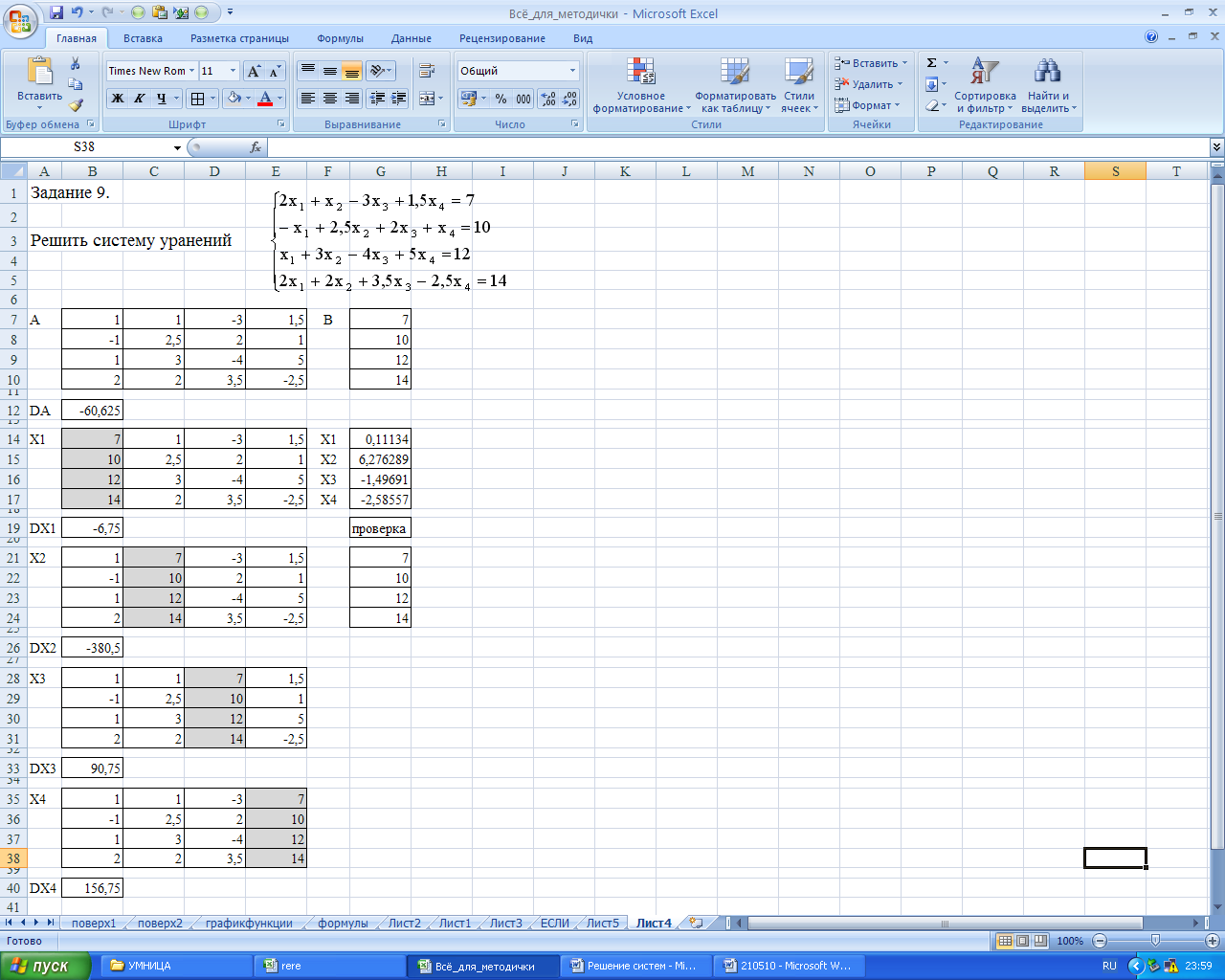
Рисунок 48

Задание 10.

Решить систему линейных уравнений Задания 9 матричным методом.

Руководство к выполнению Задания 10.

Для решения системы линейных уравнения матричным методом необходимо определить матрицу, обратную матрице коэффициентов системы. Для нахождения решения системы обратную матрицу надо умножить на столбец свободных членов заданной системы уравнения.

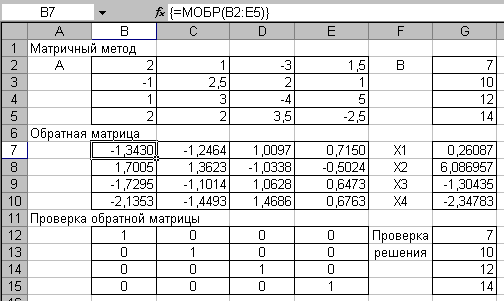
Рисунок 49

Для определения обратной матрицы надо выделить столько же столбцов и строк сколько в исходной матрице коэффициентов, то есть 4х4 ячеек. В качестве аргумента функции МОБР(Массив) выделяем массив А, вводим формулу тремя клавишам Ctrl + Shift + Enter, как и при определении проверки в предыдущей задаче.

Для проверки обратной матрицы необходимо умножить исходную матрицу А на обратную, только что найденную. Для этого выделяется блок ячеек 4 на 4 и вызывается функция МУМНОЖ(Массив1, Массив2), где Массив1 – исходная матрица А, Массив2 – обратная к ней. Вводится функция тремя клавишами Ctrl + Shift + Enter

Для определения решения выделяется столбец из 4 ячеек, вызывается функция МУМНОЖ(Массив1, Массив2), где Массив1 – обратная матрица, Массив2 – столбец свободных членов В. Вводится функция тремя клавишами Ctrl + Shift + Enter .

Проверка выполняется так же, как и в решении системы методом Крамера.

Решение показано на Рисунке 49.

Задание 11.

Решить систему линейных уравнений Задания 9 методом Гаусса.

Руководство к выполнению Задания 11.

Метод Гаусса состоит в приведении расширенной матрицы системы

к виду ,

используя арифметические вычисления.

После введения в таблицу EXCEL расширенной матрицы системы (ячейки А2:Е5) в качестве разрешающего элемента выбираем первый коэффициент первого уравнения. Если в системе первый коэффициент равен нулю, то необходимо переставить уравнения местами. Согласно Рисунку 49 получаем новые значения для первого уравнения копированием формулы _.

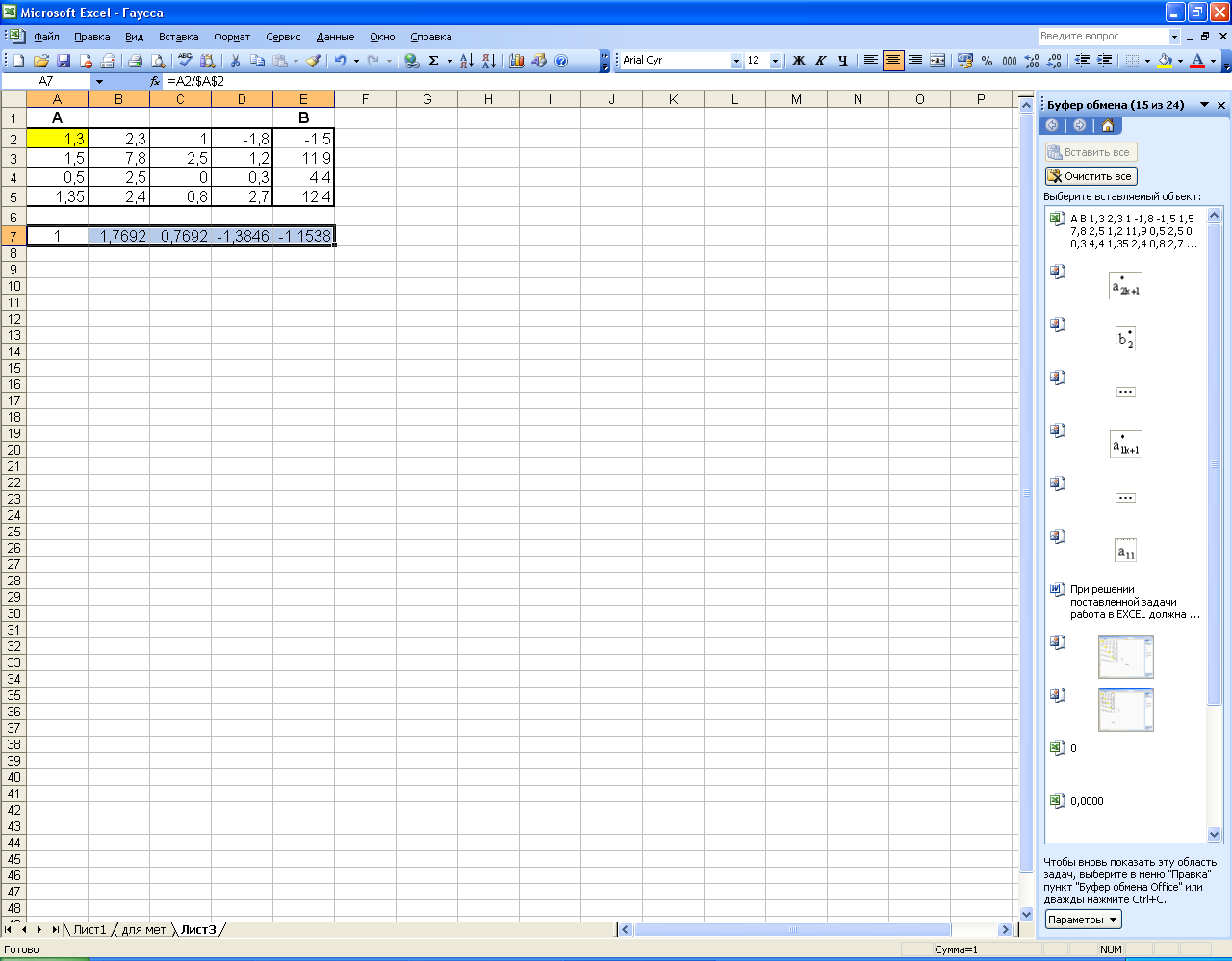
Рисунок 50

Для вычисления нового значения в ячейку А8 вводим формулу , то есть: = старое значение - новое значение с закреплением номера строки * старое значение с закреплением наименования столбца, ввод этой формулы показан на Рисунке 51.

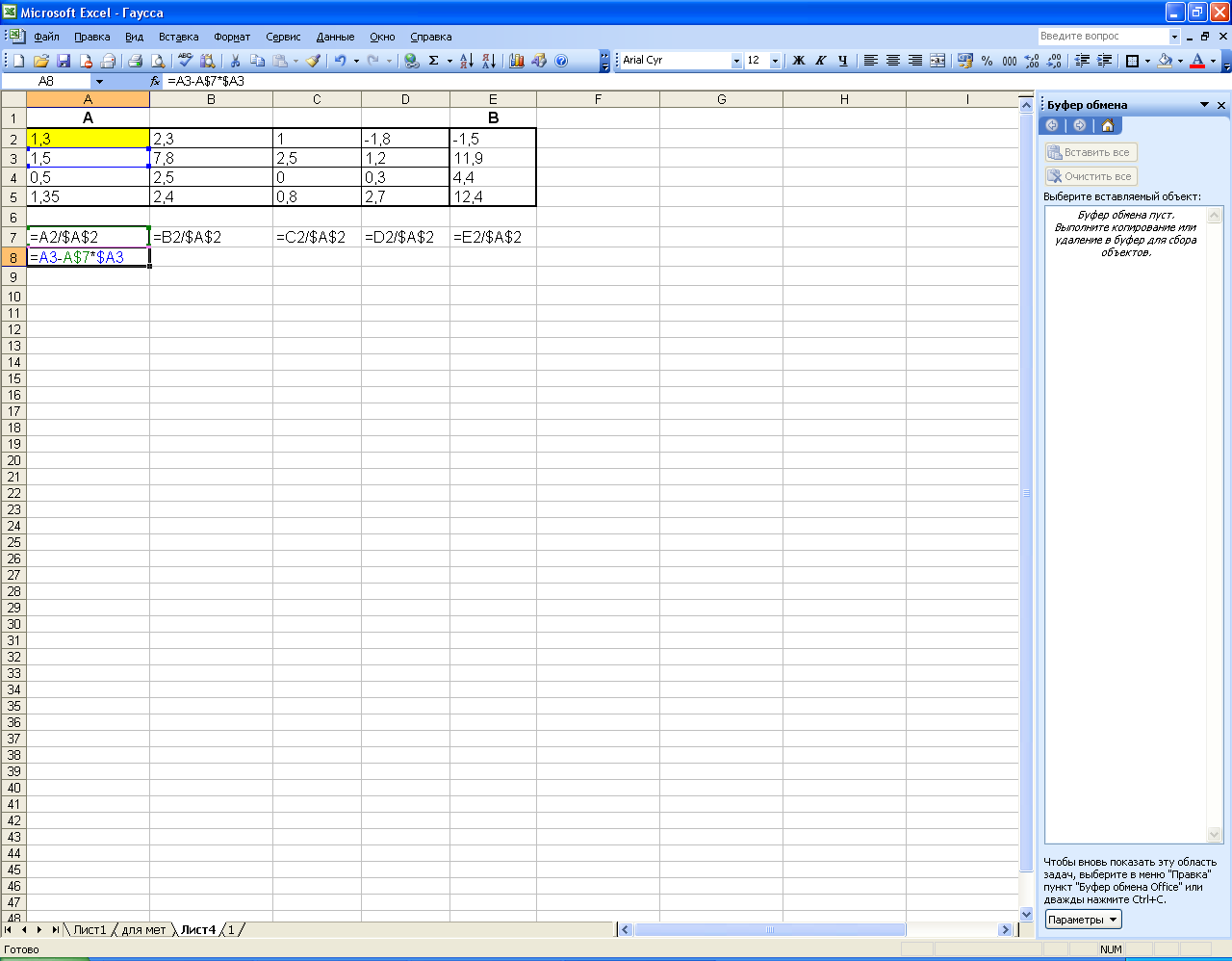
Рисунок 51

Копируем формулу на все второе уравнение и на третье, четвертое уравнения.

Рисунок 52

Затем алгоритм повторяется. Выбираем второй разрешающий элемент в ячейке В8. Выделим блок ячеек для новой матрицы и в ячейке В13 для нового значения элемента вводим формулу согласно Рисунку 53.

Рисунок 53

Копируем эту формулу в ячейки А13 и С13:Е13. В ячейку В14 согласно Рисунку 54 вводим формулу =В9-В$13*$B9. Копируем формулу в ячейки третьего и четвертого уравнения.

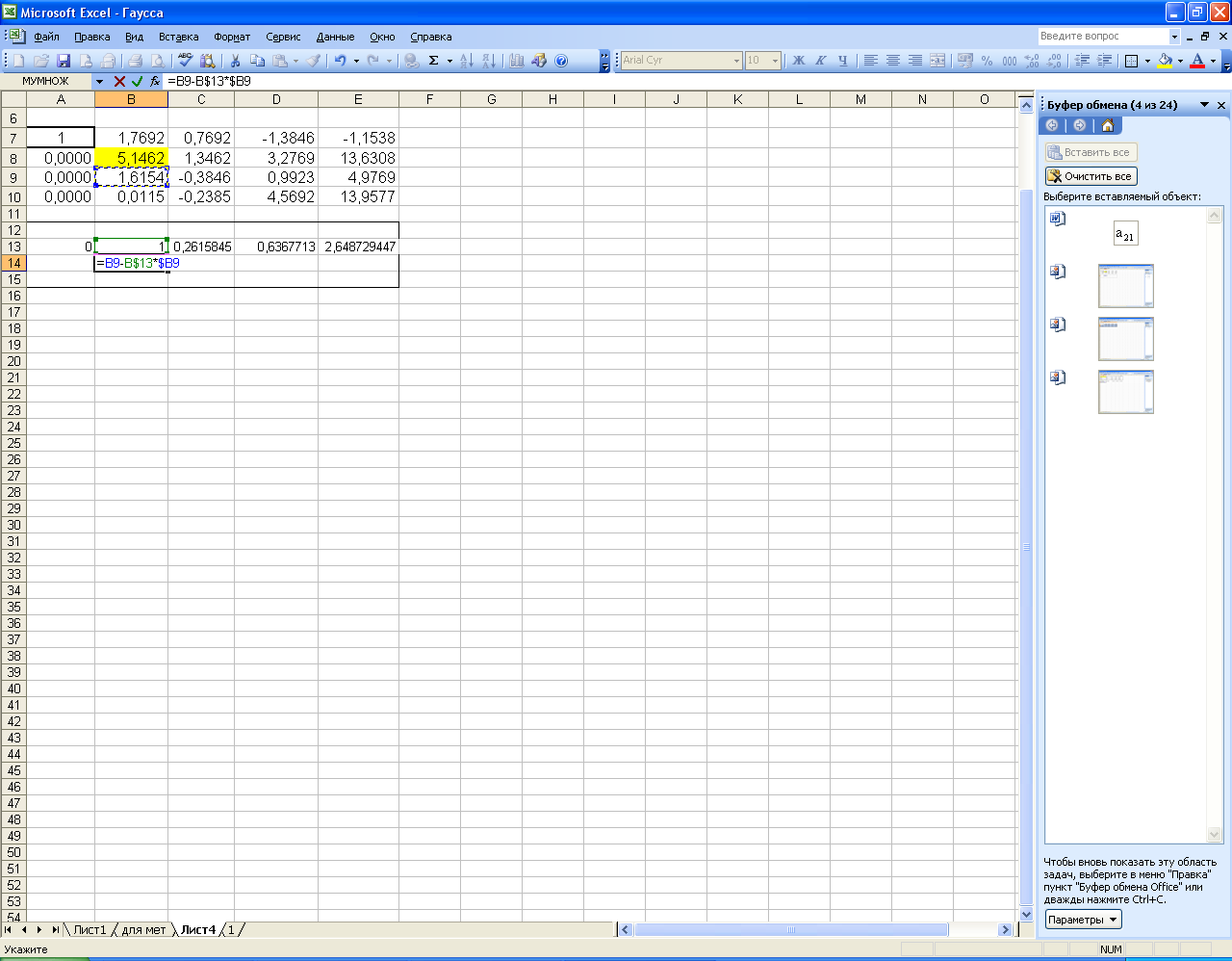
Рисунок 54

Заданную формулу из ячейки В14 копировать в диапазон первого уравнения нельзя, так как будет выдано сообщение о циклической ошибке – ссылке формулы на саму себя. Поэтому сначала командами «Копировать» и «Вставить» формулу ячейки В14 копируем в ячейку А12 согласно Рисунку 55, а затем методом «протаскивания» заполняем всю первую строку.

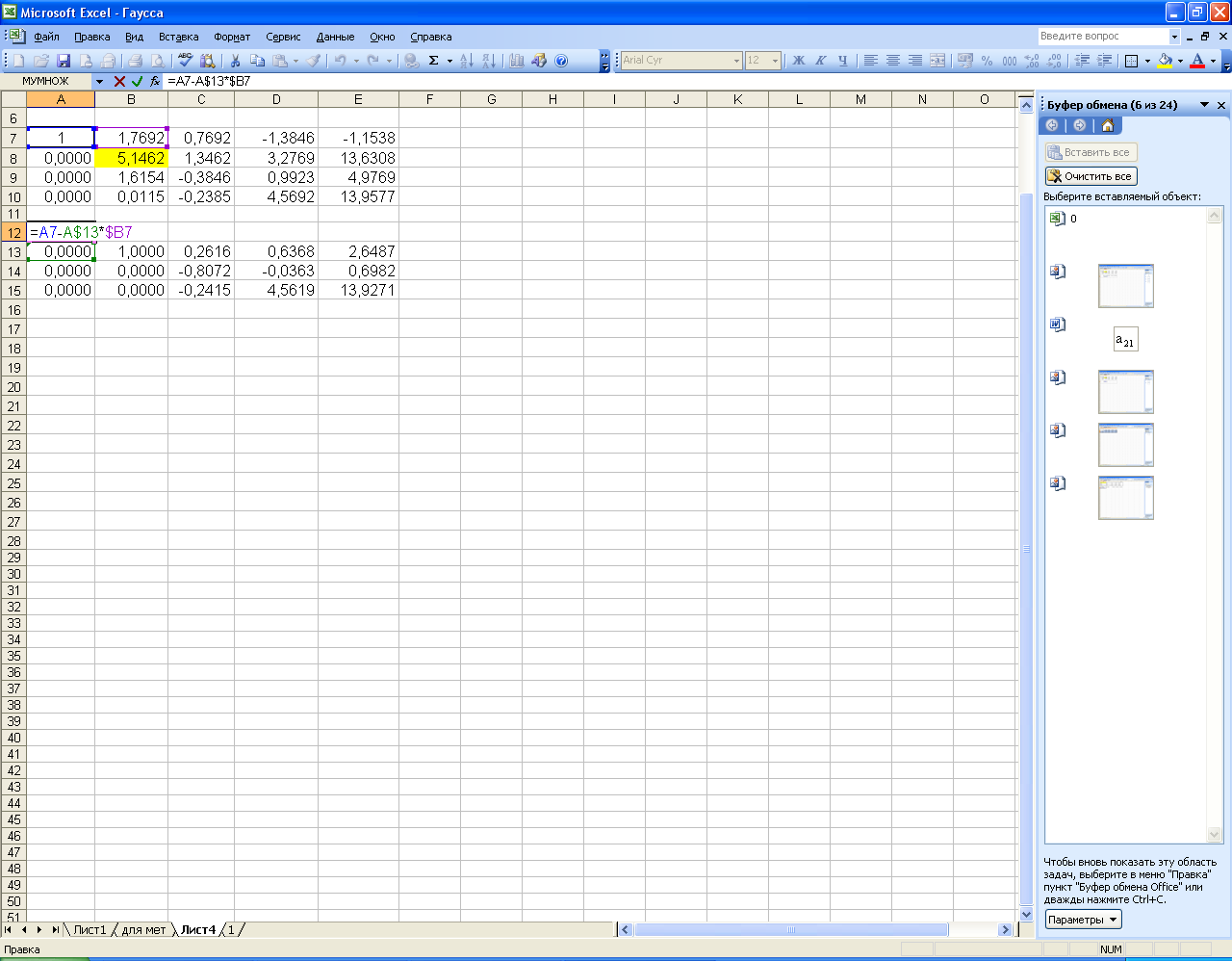
Рисунок 55

Появившееся в ячейках второй строки выделение убираем с помощью контекстного меню.

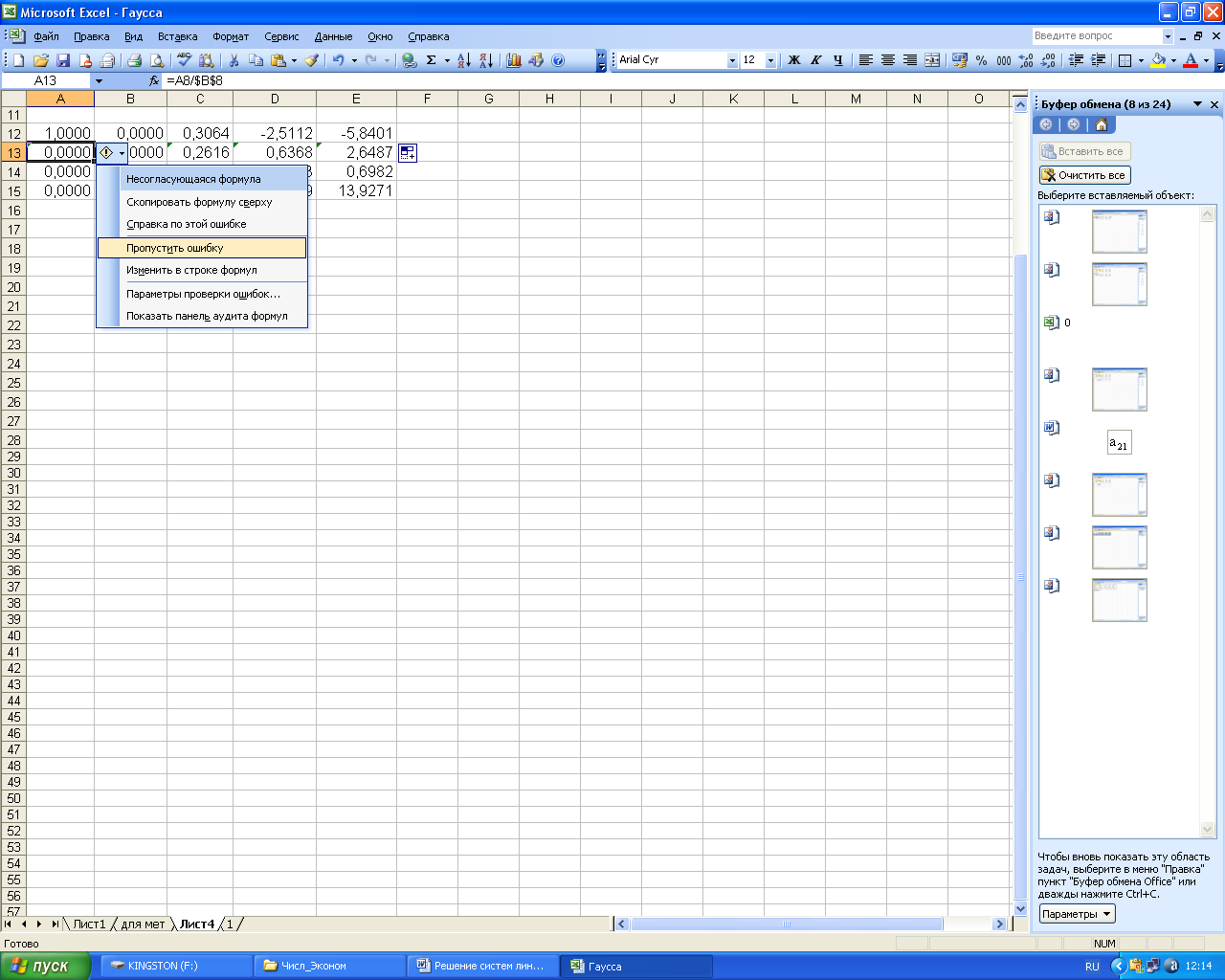
Рисунок 56

Далее выбирается третий разрешающий элемент и вводит для него формулу в блоке ячеек для новой матрицы, копируем формулу в ячейки третьей строки.

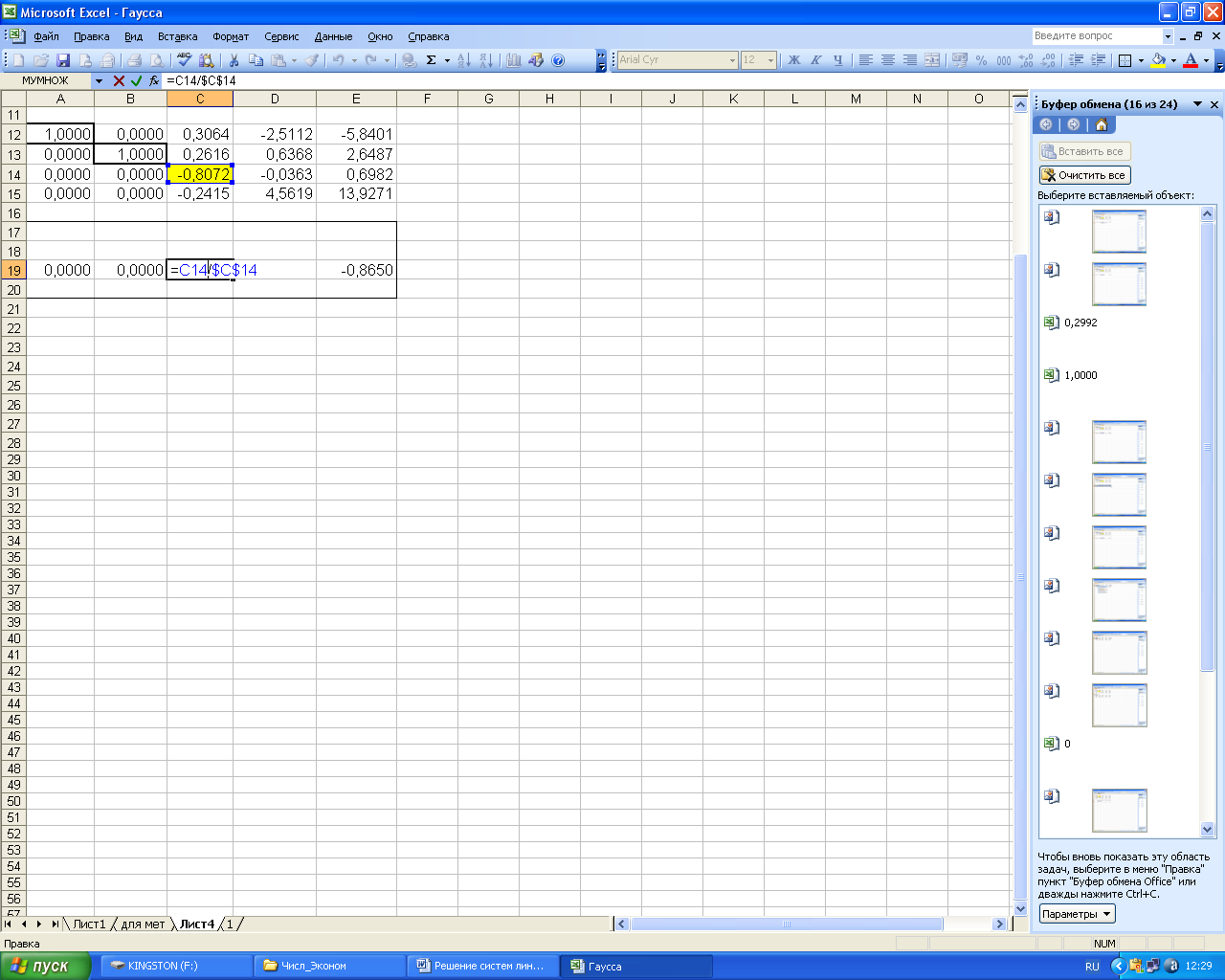
Рисунок 57

Для вычисления значений элементов четвертой строки в ячейку С20 (элемент ) вводим формулу =C15-C$19*$C15 и копируем её во все ячейки строки.

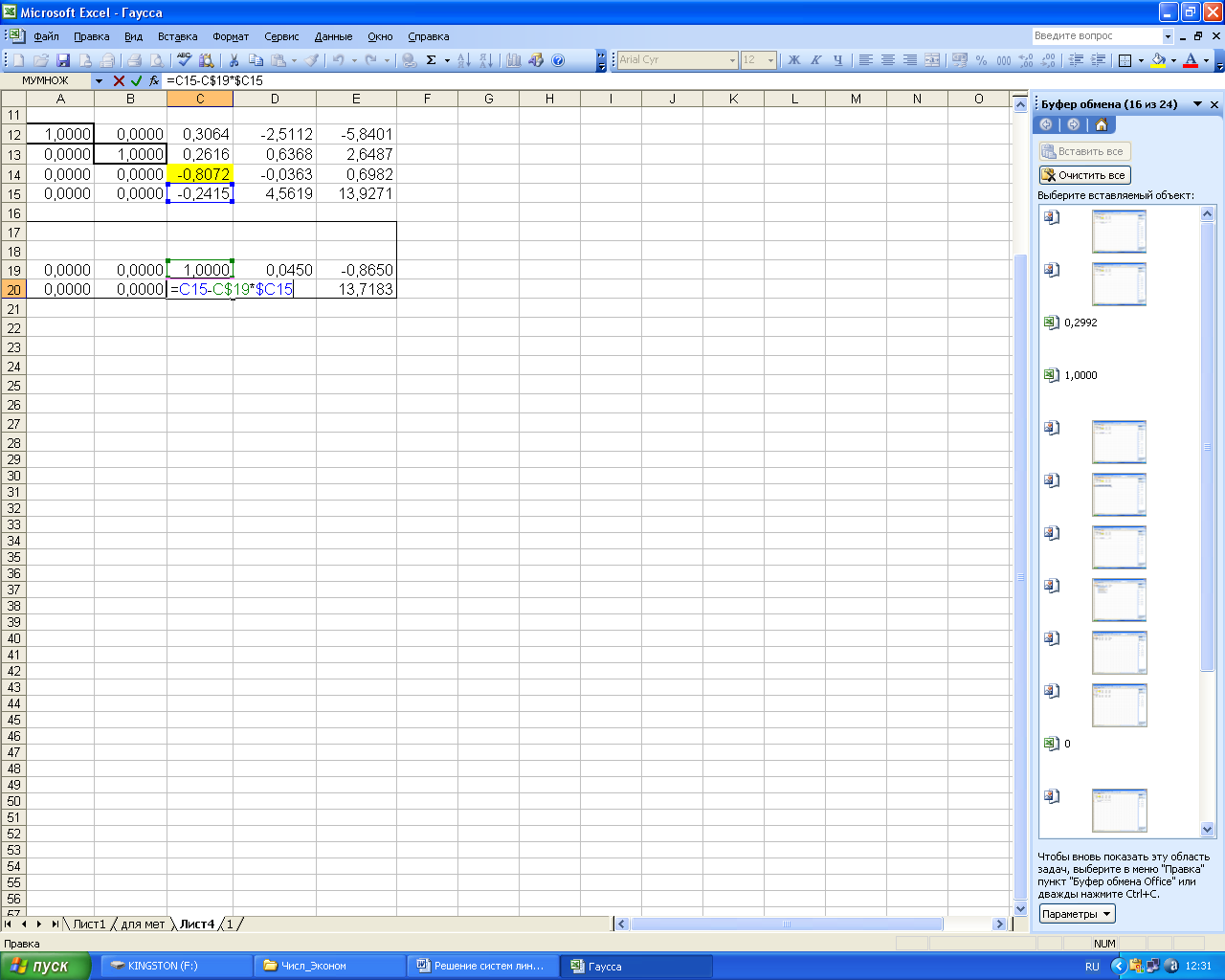
Рисунок 58

Далее не «протягиванием», а копированием и вставкой вводим формулу для элемента и «протягиваем её на ячейки первого и второго уравнений.

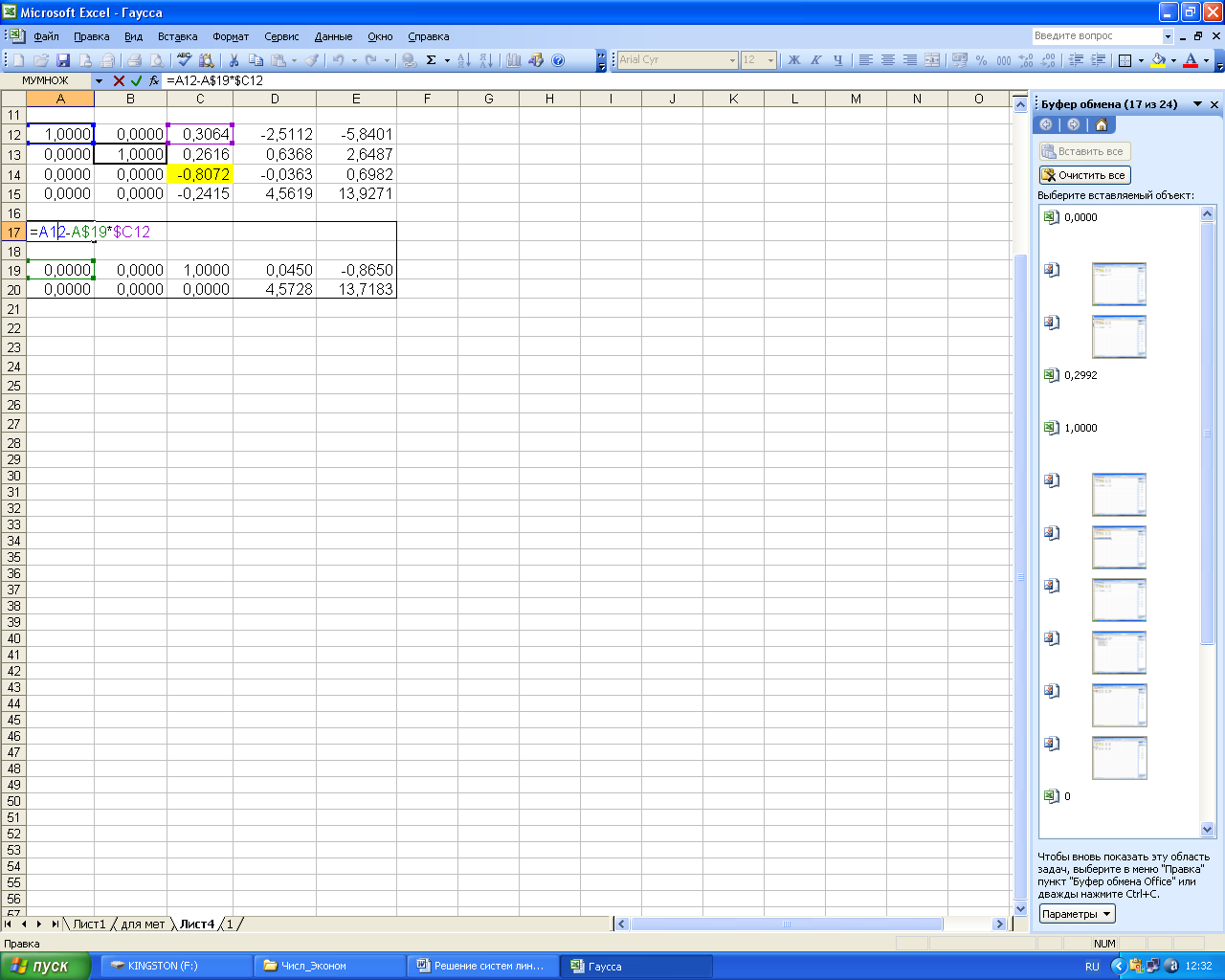
Рисунок 59

Осталось последнее уравнение. Введем формулу для и заполним ячейки четвертого уравнения

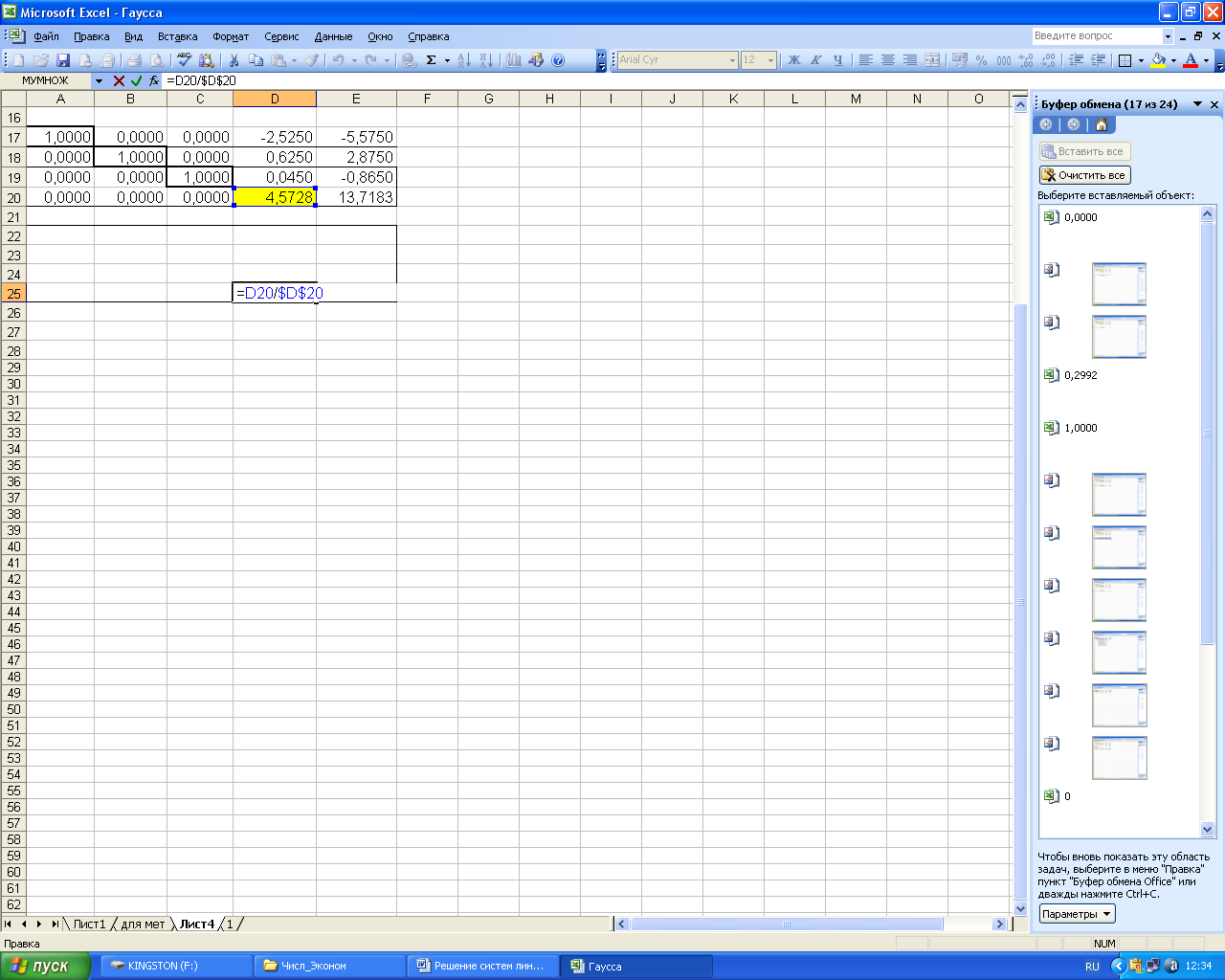
Рисунок 60

Для определения значений оставшихся коэффициентов введем в ячейку D24 формулу вычисления элемента и скопируем её на все оставшиеся ячейки.

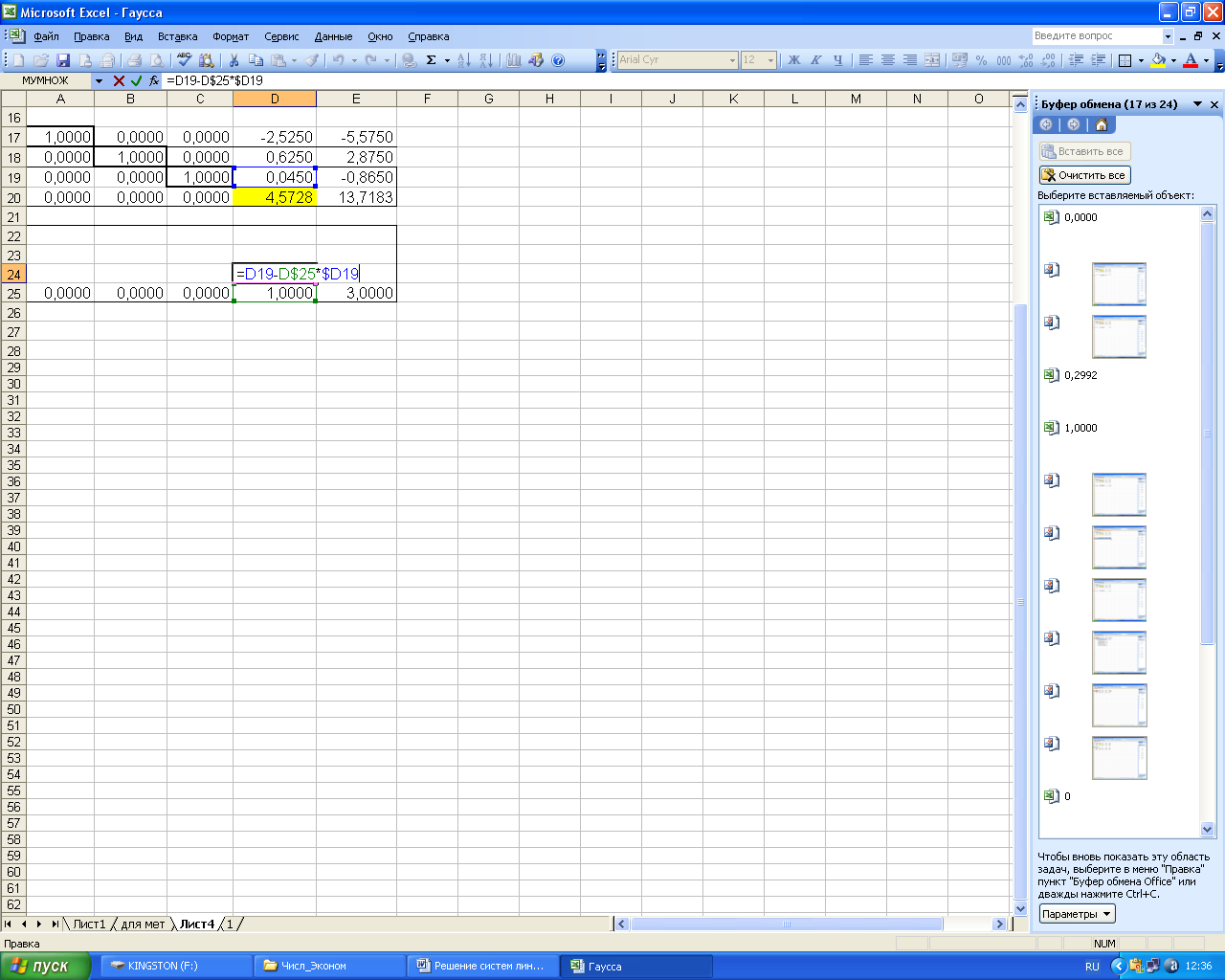
Рисунок 61

Полученный в ячейках Е22:Е25 результат является решением системы согласно Рисунку 62.

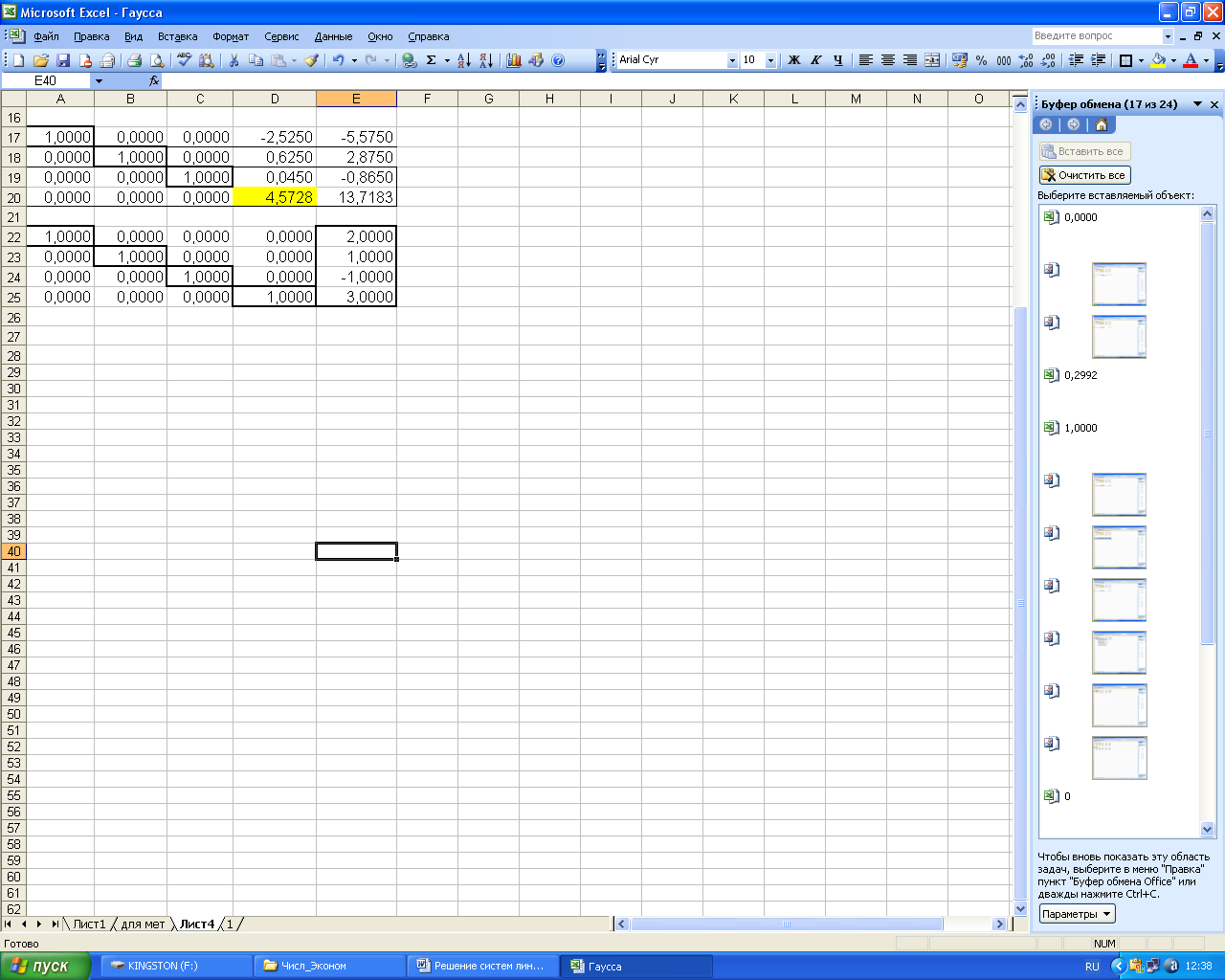
Рисунок 62

При решении поставленной задачи работа в EXCEL должна выглядеть согласно Рисунку 63:

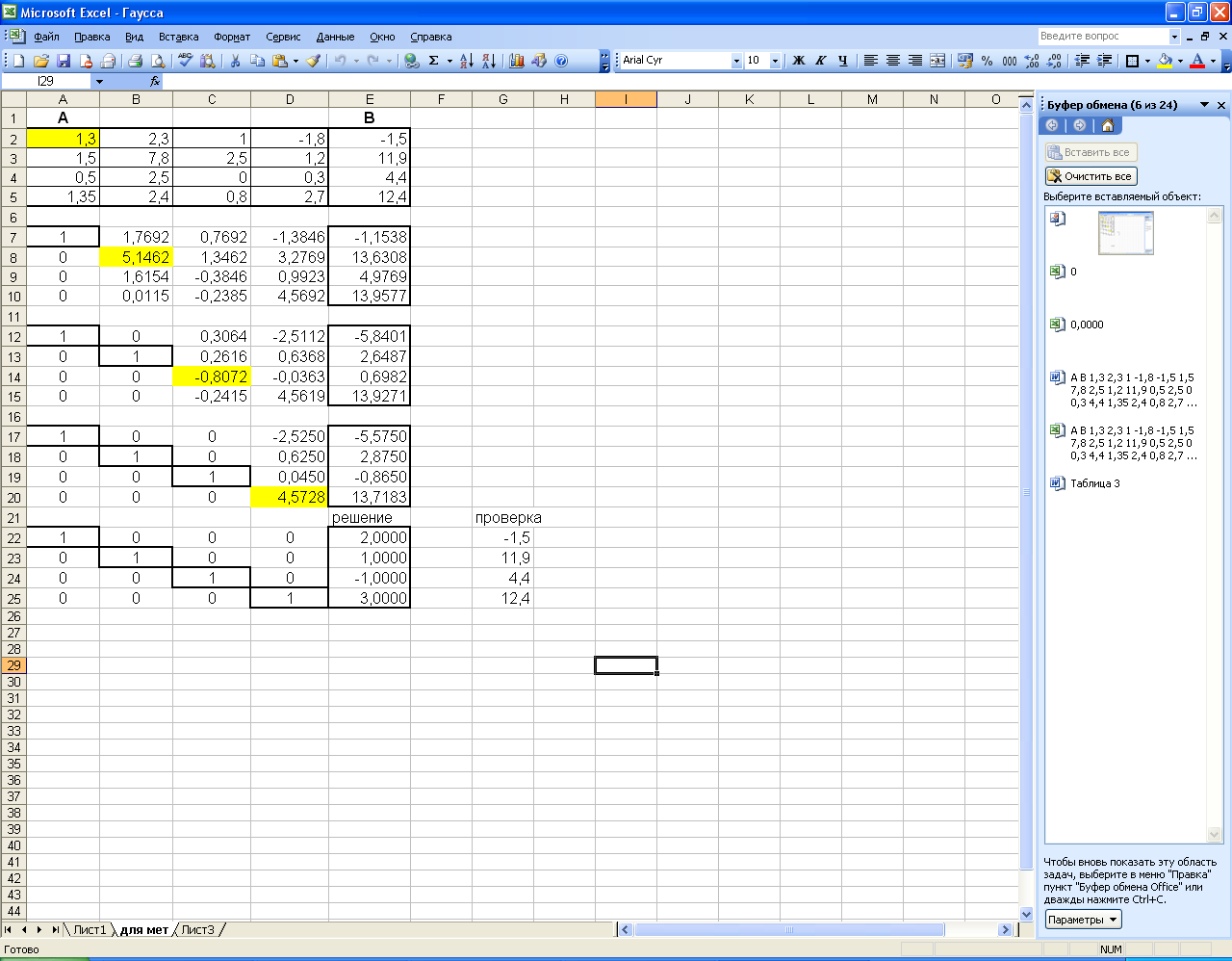
Рисунок 63