Методы расчета характеристик мсп. Решение прямой основной задачи магнитоста­тики.

Так же как и для ЭСП, для МСП - как векторного поля, важными теоремами, лежащими в основе методов расчета характеристик МСП, являются теоремы о циркуляции и о потоке вектора поля (вектора или вектора ).

Вследствие не потенциального, вихревого характера МСП, для него не удается просто и наглядно получить эти теоремы исходя из основного закона, устанавливающего фундаментальный характер сил магнитостатического взаимодействия на элементарном уровне (как это было в электро­статике - из закона Кулона).

С

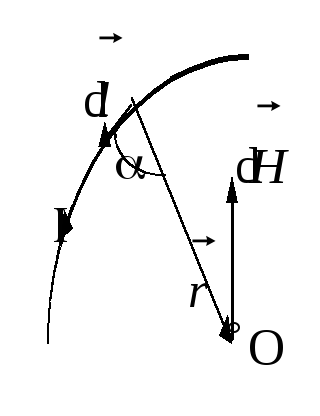
некоторым приближением, условностью, в качестве отношения, аналогичного получае­мому из закона Кулона выражению для напряженности поля точечного заряда, может служить закон Био - Савара - Лапласа. Этот закон устанавливает силу МСП, создаваемого элементарным источни­ком - элементом тока на удалении r от него:

dН = dl sin/4r² или dB = _оdlsin /4r²

где угол  - угол между векторами и .

В векторной форме закон Био - Савара - Лапласа принимает следующий вид:

d= []/4r³ или

= _оd = _о[d]/4r³

Вектор перпендикулярен как вектору так и вектору и направлен в сторону, опреде­ляемую правилом векторного произведения, или правилом буравчика (правого винта): - вращая буравчик рукоятью в плоскости векторов [ ] в направлении протекания тока, получим совпадение поступательного перемещения буравчика с направлением вектора индукции МСП.

Закон Био – Савара - Лапласа носит дифференциальный характер, и полную индукцию В_ или напряженность Н_ МСП в данной точке, создаваемую всем проводником с током, находят путем интегрирования, используя принцип суперпозиции:

_ =  _ или _рез =

Рассмотрим некоторые примеры применения закона Био - Савара - Лапласа для расчета характеристик МСП, создаваемого проводниками (с током) разной формы.

1) Прямолинейный проводник с постоянным током.

Д

ля нахождения характеристик результирующего МСП, создаваемого прямолинейным проводником с током постоянной силы  на расстоянии а от него, выберем на проводнике элемен­тарный отрезок и запишем для него закон Био – Савара - Лапласа. Векторы элементарной индукции от разных элементов проводника с током сонаправлены и векторное суммирование (интегрирование) сводится к арифметическому. Полную индукцию В от всего проводника определим путем интегрирования; для этого три переменные: , r и  в законе Био – Савара - Лапласа: сведем к одной, удобнее всего к :

r = а/sin; [ ] = dl r sin  = r²d. Подставляя их под интеграл, произведем интегрирование; переменная  для проводника изменяется в пределах от ₁ до ₂.

dВ = _оdlsin /4r² = _оIsin² аdsin /4а²sin²  = _оIsin d/4а.

В = = (_оI/4а)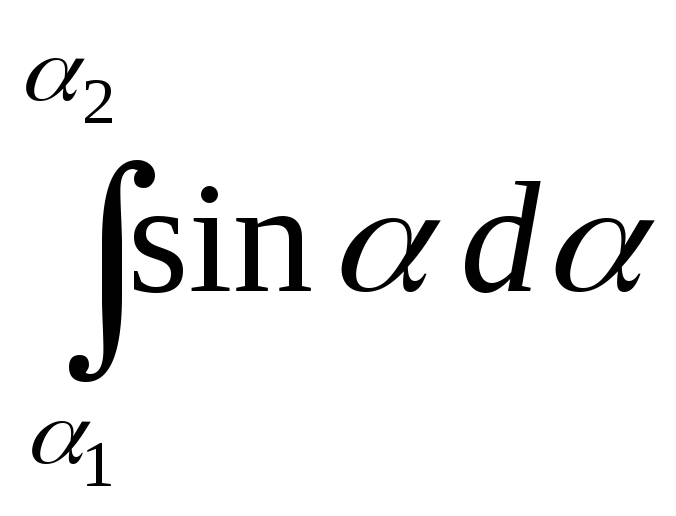 = (_оI/4а)(cos ₁ - cos ₂)

Н = В/_о = (I/4а)(cos ₁ - cos ₂) [Н] = А/м.

В

результате получили довольно простые выраже­ния для индукции и, особенно для напряженности МСП, создаваемого бесконечно длинным прямолинейным провод­ником с постоян­ным током I на удалении а от него.

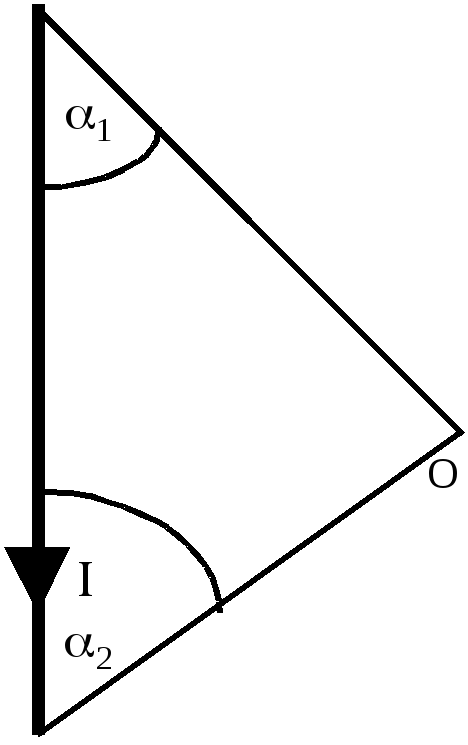
Углы ₁ и ₂ - это углы, под которыми из концов проводника видна точка, в которой ищется индук­ция и/или напряженность МСП. 2) Если проводник имеет бесконечную длину, то для него можно повторить все вышесказанное и проделанное с той лишь разницей, что пределы интегрирования (₁- ₂), характерные для конеч­ного проводника, следует заменить на пределы (0 – ). При этом очевидно, результат получается следую­щим:

В = _оI/2а и Н = I/2а