ЛЕКЦИИ (бакалавры), 1 сем -18- КАНТ– 2011

Бакалавреат-1

Конспекты лекций за 1 семестр, 2011 года.

1. Числовые множества. Натуральные числа N, целые Z, рациональные Q (m / n или периодические десятичные дроби), иррациональные ( m/n или непериодические дроби), действительные R. Числовая ось. Модуль и его свойства: |ab||a|+|b|, |ab|=|a||b|, |a/b|=|a|/|b|. Геометрический смысл величины |x₁ – x₂|. Промежутки [a,b], (a,b], (–, b], (a,+) и т.д. Окрестность конечной точки, её центр и радиус, обозначение . Проколотая окрестность. Окрестности бесконечностей –, +, .

Определение окрестностей через неравенства с модулем и без. Изображение промежутков и окрестностей на числовой оси (пустые или закрашенные точки; квадратные или круглые скобки).

2. Числовые функции. Говорят, что задана функция, если каждому значению хD соответствует единственное число у; множество D называется областью определения функции. Множество значений функции называется областью изменения Е.

Итак, функция = область определения + закон соответствия. Если область определения не указана, то подразумевается, что она совпадает с ОДЗ. Три способа задания функции. (Сомнительность графического способа (толщина линии)!)

Графиком функции называется множество точек плоскости, координаты которых (х,у) удовлетворяют условиям {xD, y = f(x)}.

Элементарные ф-ии :

.

3. Элементарные свойства функций:

а) Знак (график выше оси Х, ниже оси Х), нули функции, точки пересечения с осью Y.

б) Монотонность наглядно – «в гору», «под гору» (любые две точки на кривой удовлетворяют условию выше-ниже). Строгое определение функции, монотонной на множестве М. Пример. у=1/х не является монотонной на области определения!!!

в) Ограниченность на множестве М (сверху, снизу, просто), геометрический смысл, точное определение. Кванторы , , определение ограниченности, отрицание этого определения.

ТЕОРЕМА. Сумма и произведение ограниченных на М функций также ограничены на этом множестве. ДОК-ВО.

Вопрос: верно ли это для частного двух ограниченных на М функций? ( tgx = Sinx/Сosx).

Вопрос: Почему y = Sinx , y = x² ограничены снизу на R, а их произведение – нет.

г) Периодичность, определение и примеры. не является периодической.

д) Обратная функция. Определение: Пусть дана функция y = f(x), xD, yE и пусть уравнение f(x) = y имеет единственное решение x = g(y) для любого yE . Тогда эта зависимость называется обратной функцией для функции y = f(x), xD, yE. Основные тождества. Графики взаимно обратных функций – это одна и та же кривая!

Не всякая функция имеет обратную.

ТЕОРЕМА. Всякая монотонная функция имеет обратную. Объяснение на графике.

ЗАДАЧА. Привести пример немонотонной функции, имеющей обратную.

4. Пределы функций.

Процессы на оси Х: x x₀–0 , x x₀+0 , x – , x+ . (Изобразить на оси Х точки со стрелочками, процессы изображать движением рук). Возможны также случаи х х₀ и х   . Пример. х=(–1)^пп

Аналогично процессы на оси Y: y=f(x) b , – , + .

Графическое определение пределов функции.

Пример. Дать графическое определение предела

.

Изображается кривая, три точки (на оси Х, на оси Y и на кривой) и три стрелки, соответствующие процессам.

Аналогичным образом определяются другие типы пределов.

Примечание. Процесс х а означает, что х может стремится к а как справа так и слева; процесс х  означает, что х может стремится как к + так и к – .

Способы вычисления простеньких пределов: а)Подстановка, б)сокращение и подстановка, в)деление на старшую степень прих .

Замечание. Переменная, по которой вычисляется предел, может быть любой буквой.

ОЧЕВИДНЫЕ арифметические свойства пределов (линейность операции lim, предел произведения, частного).

5. Бесконечно малые и бесконечно большие функции и их свойства.

Определение (предел равен 0 или ), примеры (графические и аналитические). Обязательное указание процесса.

Степенные, показательные, логарифмические бесконечности.

ТЕОРЕМЫ о связи б.м. и б.б. функций. без д-ва, человеческое обоснование (если одно яблоко поделить на 1000 человек, сколько получит каждый?).

ТЕОРЕМА о сумме б.м. и о произведении б.м. на ограниченную. Без д-ва.

ТЕОРЕМА О связи конечного предела с б.м. функцией. f(x)Af(x)=A+(x). Без д-ва. Пример вычисления предела при х  : 2+б.м.

6. Сравнение бесконечно малых и бесконечно больших величин.

Житейский пример. Пусть две положительных величины таковы, что m/n = 0,001. Какая из этих величин меньше и во сколько раз? Аналогичный вопрос для a/b=1000.

Сравнения б.м. и б.б. функций. Определение по аналогии соотношений

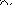
. (для запоминания: f(x) – Очень МАЛАЯ по сравнению с g(x) в данном процессе)

Примеры. Сравнить величины

Важное определение: .

Из него вытекает: !!!

Шкала бесконечностей.

Из графика видно, что . Используя это, найдем

ТЕОРЕМА о замене сомножителя ненулевой константой. Если f(x) А  0 при х х₀ , то f(x)g(x)Ag(x) при х х₀ . Д-во.

ТЕОРЕМА о сохранении главного слагаемого. f(x) + o(f(x))  f(x). Д-во.

ПРИМЕЧАНИЕ. Сохранение главного слагаемого под знаком функции недопустимо для показательных функций, т.е. exp( f(x) + o(f(x)) ) не всегда  exp( f(x)) !!!!!!!

Определение. Если f(x) = g(x) + o(g(x)) при хх₀ , то функция g(x) называется главной частью функции f(x) (или её асимптотикой) при х х₀ (или её асимптотикой в точке х₀).

Пример. Найти асимптотики в нулях, в особых точках и на бесконечности для функций.

. Чему равен y при x = 1000 ?

Построить эскизы графиков по этим асимптотикам.

7. Свойства функций, имеющих конечный предел.

ТЕОРЕМА. Функция, имеющая конечный предел в некотором процессе, ограничена в этом процессе, т.е в некоторой (проколотой) окрестности предельной точки.

Без доказательства. Демонстрация на примере f(x)2 при x - 

ТЕОРЕМА. Если неотрицательная в некотором процессе функция имеет предел в этом процессе, то этот предел неотрицателен.

Без доказательства, с графической иллюстрацией.

Контрпример для ПОЛОЖИТЕЛЬНЫХ функций.

Следствие. Переход к пределу в неравенствах.

Д-во с использованием предыдущей теоремы

ТЕОРЕМА. Если предел функции положителен, то и сама функция положительна, начиная с некоторого момента процесса. Графическая иллюстрация.

ТЕОРЕМА о двух милиционерах. Формулировка и графическая иллюстрация

Первый замечательный предел. . Всё с выводом.

Второй замечательный предел . (без вывода).

Использование второго замечательного предела для вывода следствий

Следствия.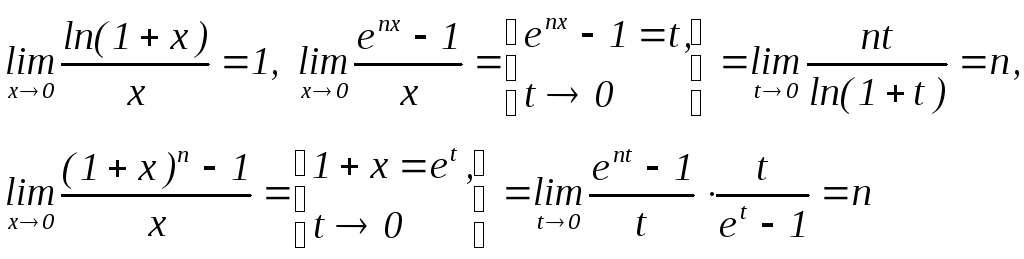

8. Асимптотические формулы.

Напомнить соотношения: 1)

2) f(x)(x)=o(f(x)) , x  x₀ .

При х  0 имеют место формулы (некоторые с выводом):

Sinx = x+ o(x),  Cosx = 1+ x²/2 + o(x² ), tgx = x + o(x),

ln(1+x) = x + o(x), e^x = 1 + x + o(x),   (1 + x)ⁿ = 1+nx+o(x) .

9. Непрерывные функции.

Определение. Функция y = f(x) называется непрерывной в точке х₀ , если

а) она определена в некоторой окрестности этой точки,

б) 

Непрерывность СПРАВА и СЛЕВА. Не давать строгие определения. Лучше всё показать на картинках

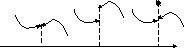
Вывод. Для непрерывной функции предел вычисляется подстановкой:

.

Дать определение «приращения в точке». Примеры. Геометрический смысл.

Печальный опыт. Больше половины публики не может найти у для у=1/х .

Другое определение непрерывности: Бесконечно малому х соответствует бесконечно малое у .

Геометрический смысл непрерывности функции: График рисуется, не отрывая руки от бумаги.

Тонкость: не является непрерывной в нуле! (Она непрерывна справа).

10. Основные теоремы о непрерывных функциях.

ТЕОРЕМА о локальной ограниченности. Д-во. Нарисуйте график функции, которая непрерывна в точке х=2. Покажите, что функция ограничена в некоторой окрестности этой точки (график между двумя горизонталями)

ТЕОРЕМА о сохранении знака непрерывной функции. Д-во. Нарисуйте график функции, которая непрерывна в точке х=2. и f(2)>0. Покажите, что f(x)>0 также и в некоторой окрестности точки х=2.

ТЕОРЕМЫ об арифметических операциях с непрерывными функциями. Сформулировать и предупредить, что для частного непрерывных функций имеются оговорки.

11 Сложная функция. Непрерывность.

Определение. Пусть каждому х из множества D соответствует единственное z из Е (задана z=g(x) на множестве D), а каждому z из Е соответствует единственное y (задана y = f(z) на множестве Е). Это означает, что задана сложная функция y=f(g(x)), xD. Функция f( ) – внешняя, функция g( ) – внутренняя.

Условие существования: Внешняя функция должна быть определена на множестве значений внутренней функции: сложная функция y = ln(–x²) не существует.

Сложная функция называется также суперпозицией.

ТЕОРЕМА о непрерывности сложной функции. Пусть задана сложная функция y = f(g(x)) и пусть внутренняя функция z=g(x) непрерывна в точке х₀ , а внешняя функция f(z) непрерывна в соответствующей точке z₀ = g(x₀). Тогда сложная функция будет непрерывной в точке х₀ .

ОБОСНОВАНИЕ. Дадим х малое приращение х. Тогда функция z=g(x) получит малое (в силу непрерывности g(x)) приращение z. А тогда функция y=f(z) получит малое (в силу непрерывности f(z)) приращение у. Следовательно, малому приращению х соответствует малое приращение у сложной функции y=f(g(x)) , а это означает, что сложная функция непрерывна.

12. Обратная функция. Непрерывность.

Определение обратной функции как решения уравнения y = f(x) относительно х.

Основные тождества для взаимно обратных функций.

Графики взаимно обратных функций – это одна и та же кривая.

ТЕОРЕМА о непрерывности обратной функции. Пусть y = f(x) строго монотонна и непрерывна на (а, b). Тогда у этой функции существует обратная функция, и эта обратная функция является непрерывна.

Д-во крестьянское: 1) существование, т.к. строгая монотонность, 2) непрерывность, т.к. графики взаимообратных функций это одна и та же кривая. Их оба можно нарисовать не отрывая карандаша от бумаги.

13. Непрерывность элементарных функций.

6. Напомнить графики линейной функции, экспоненты и показательной функции, тригонометрических функций. «А теперь самостоятельно напишите: Функция такая-то непрерывна там-то». Рассмотреть

14. Классификация точек разрыва. (Обязательно картинки!!!)

НАПОМИНАНИЕ. Если функция y=f(x) непрерывна в точке х=а , то существуют односторонние пределы и они равныf(a).

ОПРЕДЕЛЕНИЕ. Точка х=а называется точкой устранимого разрыва, если односторонние пределы в этой точке существуют и равны, а значение функции в этой точке не совпадает со значением этих пределов либо функция вообще не определена при х=а.

Примеры. y=sgn²(x) ; .

Обсуждение. Почему разрыв называется устранимым.

ОПРЕДЕЛЕНИЕ. Точка х=а называется точкой разрыва первого рода (скачком), если односторонние пределы существуют и различны. В самой точке функция может быть либо определена, либо не определена.

Примеры. y=sgn(x) ,

(Кусочно-заданная функция, >f:=x–>piecewise(x<1,1-x,x-1); )

ОПРЕДЕЛЕНИЕ. Точка х=а называется точкой разрыва второго рода, если хотя бы один из односторонних пределов не существует.

Примеры. .

.Мнемоническое правило. Разрыв 1-го рода МАЛЕНЬКИЙ, 2-го рода БОЛЬШОЙ (2>1).

15. Функции непрерывные на отрезке.

ОПРЕДЕЛЕНИЕ. Пусть функция определена в правой полуокрестности точки а и пусть . Тогда функция называется непрерывной в точкех=а справа. Аналогичное определение непрерывности в точке слева.

Примеры:    , ,

ОПРЕДЕЛЕНИЕ. Функции y=f(x) называется непрерывной на отрезке [a, b], если её график, соединяющий точки (a,f(a)) и (b,f(b)) можно нарисовать, не отрывая карандаша от бумаги. Задача. Нарисовать график функции, непрерывной на отрезке [–1, 3].

Свойства функций, непрерывных на отрезке.

• Теорема Коши о промежуточном значении. Пусть функция y=f(x) непрерывна на [a,b] и принимает на концах отрезка значения разных знаков. Тогда существует с(a,b) такая, что f( c) = 0. Задача. Нарисовать такую функцию и найти точку х=с. Сколько таких точек может быть?

Примеры аналитические и графические.

Контрпримеры: у=1/(х–2) на [1;3] , у= sgnx–0,5 на [0; 1]

• 1-я теорема ВЕЙЕРШТРАССА. Если функция f(x) непрерывна на отрезке [a,b], то она ограничена на этом отрезке. Самостоятельно убедиться на графике.

Примеры и контрпримеры. а) нет отрезка, б) нет непрерывности

• 2-я теорема ВЕЙЕРШТРАССА. Если функция y=f(x) непрерывна на [a,b], то она достигает на этом отрезке свои max u min. Самостоятельно убедиться на графике.

Примеры и контрпримеры. y=Sgn(x)–x , на отрезке [–1; +1].

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ.

Определение производной. Пусть функция y=f(x) определена в некоторой окрестности точки х₀.

а) Составим приращение функции в этой точке y=f(x₀+x)–f(x₀).

б) Поделим это приращение на х.

в) Найдем предел отношения у/х при х .

Если этот предел существует, то он называется производной функции f(x) в точке х₀. и обозначается через f’(x₀).

Итак, по определению

Определение. Функция y=f(x) наз. дифференцируемой в точке х₀, если существует f’(x₀).

Замечание. Из определения производной вытекает, что дифференцируемая в точке функция должна быть определена в некоторой окрестности этой точки.

*Механический смысл производной: S(t)– перемещение, V(t)=S’(t)– скорость.

Производные по определению (при наличии времени).

А) Производная от константы = 0.

В) Степенная функция у=х^п

…

С) Функции

ТЕОРЕМА. Если функция y=f(x) дифференцируема в точке х₀ , то она непрерывна в этой точке.

Д-во: 1) Дифф  определена в некоторой окрестности точки х₀. (см. опр-е производной). 2) По условию существует предел от прих. Это означает, что y  , т.к иначе предела не существовало бы. След. б/малому приращению по Х соответствует б/малое приращение по Y, т.е. функция непрерывна.

ОБРАТНАЯ ТЕОРЕМА неверна:

У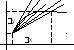равнение касательной. Касательная – это прямая, положение которой определяется предельным положением секущей (рис.)

Вывод: .

• Кривая, имеющая в точке х₀ касательную, называется гладкой в этой точке.

• Дифференцируемая функция имеет гладкий график.

• Гладкая кривая является непрерывной; но непрерывная кривая не обязательно гладкая (ломаная линия).

Геометрический смысл производной: Коэффициент при х , т.е. f’(x₀) - это тангенс угла наклона касательной к оси Х; знаки тангенса, знаки производной, возрастание и убывание функции.

Производные от суммы, произведения, частного.

Предварительные слова: Для любой функции

u(x+x) – u(x) = u  u(x+x) = u(x) + u.

ТЕОРЕМА. Пусть функции u(x), v(x) дифференцируемы в точке х. Тогда их сумма, произведение и частное также будут дифференцируемы в точке х, причем

(u+v)’=u’+v’,  (uv)’=u’v+v’u, (u/v)’=(u’v–v’u)/v² .

В последнем случае предполагаем, что v(x)0 .

Д-во для суммы.

Пример применения: (tgx)’ , (ctgx)’ .

Производная от сложной функции y=f(z), где z=g(x).

Теорема. Пусть внутренняя функция z=g(x) дифференцируема в точке х₀ , а внешняя функция y=f(z) дифференцируема в соответствующей точке z₀=g(x₀). Тогда сложная функция y=f(g(x)) дифференцируема в точке х₀ и при этом производная в этой точке равна

y’=f’(z₀)g’(x₀) .

Д-во: Дадим х₀ приращение х. Тогда внутренняя функция получит приращение z=g(x₀+x)–g(x₀), а внешняя функция получит приращение y=f(x₀+z)–f(z₀). Т.к. g(x) дифференцируема, то она непрерывна, и поэтому z при x. Далее по определению

= f’(z₀)g’(x₀).

Предполагается без д-ва, что сложная функция определена в некоторой окрестности точки х₀ и что при стремлении x к нулю приращение z   , не обращаясь в нуль!

Примеры применения теоремы.

.

Производная обратной функции. Теорема. Если функция у=у(х) дифференцируема в точке х₀, то обратная функция х=х(у) также является дифференцируемой в соответствующей точке у₀ и при этом y’(x₀)x’(y₀)=1.

Д-во: Если прямая функция гладкая, то обратная функция также является гладкой, т.к. это одна и та же кривая (см. рис.). Согласно геометрическому смыслу производной

y’(x₀)=tg , x’(y₀)=tg=tg(=ctg. .

Отсюда y’(x₀) x’(y₀)= tg  ctg=1.

Линеаризация функции.

Теорема о линеаризации. Если функция y=f(x) дифференцируема в точке х₀ , то имеет место асимптотическая формула линеаризации (АФЛ)

Д-во: По условию существует производная, т.е.

…