А+В=В+А; A+(B+C)=(A+B)+C; A+0=A; x(A+B)=xA+xB; (x+y)A=xA+yA; A-A=0; x(yA)=(xy)A

Умножать друг на друга можно только те матрицы, для которых число столбцов первого сомножителя равно числу строк второго сомножителя. Сточку умножаю на стобец, а элемент - сумма умножений.

A*B!=B*A; A*B*C=A*(B*C)=(A*B)*C; A*(B+-C)=A*B+-A*C; A*E=E*A=A; E-единичн. матр.

Произведение любой матрицы и единичной матрицы подходящего размера равно самой матрице: A E = E A = A

Квадратная матрица в нулевой степени дает единичную матрицу того же размера:A^0 = E

При умножении матрицы на обратную ей тоже получается единичная матрица:A A^-1= E

Единичная матрица получается при умножении ортогональной матрицы на её транспонированную матрицу:

A A^T = E

Определитель единичной матрицы равен единице

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц, то есть, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарными преобразованиями строк называют:

перестановку местами любых двух строк матрицы;

умножение на ненулевую константу любой строки матрицы;

прибавление к любой строке матрицы другой строки, умноженной на ненулевое число

Матрицы A и B называют эквивалентными матрицами если от матрицы A к матрице B перешли с помощью элементарных преобразований над строками и обозначают A ~ B.

Ступенчатая матрица — матрица, имеющая m строк, у которой первые r диагональных элементов ненулевые, r ≤ m, а элементы, лежащие ниже диагонали и элементы последних m − r строк равны нулю

Определение. Если у ступенчатой матрицы все опорные элементы равны единице, а под опорными элементами стоят нули, то матрица имеет ступенчатый вид ГауссаВид Гаусса ступенчатый.

Привести матрицу A к ступенчатому виду Гаусса можно при помощи элементарных преобразований строк.

Каждой квадратной матрице A ставится в соответствие число /А/, называемое ее определителемОпределитель матрицы, так, что выполняются следующие свойства:

1) если к матрице применить элементарное преобразование строк первого типа, то определитель изменит знак на противоположный;

2) если к матрице применить элементарное преобразование строк второго типа, то определитель не изменится;

3) если строку матрицы умножить на число, то определитель умножится на это число;

4) определитель верхнетреугольной матрицы равен произведению элементов, стоящих на ее главной диагонали.

Определитель Гауссом: Привести в верхнетреугольный вид, перемножить числа на главной диаганали.

Пусть A — квадратная матрица порядка n. Матрица A^-1, удовлетворяющая вместе с заданной матрицей A равенствам: A^-1*A=A*A^-1=E называется обратной. Матрицу A называют обратимой, если для нее существует обратная, в противном случае — необратимой (Если определитель равен нулю).

Обратная матрица с помощью алг дополнений - метод Крамера

Система может иметь единственное решение.

Система может иметь бесконечное множество решений. Например, . Решением этой системы является любая пара чисел, отличающихся знаком.

И третий случай, когда система вообще не имеет решения. Например, , если бы решение существовало, тоx₁ + x₂ равнялось бы одновременно нулю и единице.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

Условие существования ненулевого решения системы n однородных уравнений с n неизвестными тогда когда определитель=0

Для двух векторов плоскости эквиваленты следующие утверждения:1) векторы линейно независимы;2) векторы образуют базис;3) векторы не коллинеарны;4) векторы нельзя линейно выразить друг через друга;5) определитель, составленный из координат данных векторов, отличен от нуля.

Соответственно, эквивалентны следующие противоположные утверждения:1) векторы линейно зависимы;2) векторы не образуют базиса;3) векторы коллинеарны;4) векторы можно линейно выразить друг через друга;5) определитель, составленный из координат данных векторов, равен нулю.

Рассмотрим более подробно новый, пятый пункт: два вектора плоскости  коллинеарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю

Два вектора плоскости линейно зависимы тогда и только тогда, когда они коллинеарны .

Для того чтобы два вектора плоскости  были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны 

Любой вектор плоскости  единственным образом раскладывается по базису :, где  – действительные числа. Числа  называют координатами вектора в данном базисе.

Также говорят, что вектор  представлен в виде линейной комбинации базисных векторов. То есть, выражение  называют разложением вектора  по базису  или линейной комбинацией базисных векторов.

Определение: три вектора называются компланарными, если существует плоскость, которой они параллельны. Здесь логично добавить, что если такой плоскости не существует, то и векторы будут не компланарны.

Компланарные векторы всегда линейно зависимы, то есть линейно выражаются друг через друга.

три некомпланарных вектора всегда линейно независимы, то есть никоим образом не выражаются друг через друга. И, очевидно, только такие векторы могут образовать базис трёхмерного пространства.

Определение: Базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов , взятых в определённом порядке, при этом любой вектор пространства единственным образом раскладывается по данному базису , где  – координаты вектора  в данном базисе

Для трёх векторов пространства эквиваленты следующие утверждения:1) векторы линейно независимы;2) векторы образуют базис;3) векторы не компланарны;4) векторы нельзя линейно выразить друг через друга;5) определитель, составленный из координат данных векторов, отличен от нуля.

Векторы образуют базис в трехмерном пространстве когда определитель неравен нулю

Ответ напрашивается сам собой. Система линейных уравнений является однородной, если свободный член каждого уравнения системы равен нулю. Например:

Решить однородную систему линейных уравнений

Решение: чтобы решить  однородную систему необходимо записать матрицу системы и с помощью элементарных преобразований привести её к ступенчатому виду. Обратите внимание, что здесь отпадает необходимость записывать вертикальную черту и нулевой столбец свободных членов – ведь что ни делай с нулями, они так и останутся нулями:

(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –3.

(2) К третьей строке прибавили вторую строку, умноженную на –1.

Делить третью строку на 3 не имеет особого смысла.

В результате элементарных преобразований получена эквивалентная однородная система , и, применяя обратный ход метода Гаусса, легко убедиться, что решение единственно.

Ответ: 

Сформулируем очевидный критерий: однородная система линейных уравнений имееттолько тривиальное решение, если ранг матрицы системы (в данном случае 3) равен количеству переменных (в данном случае  – 3 шт.).

азисом системы векторов A₁ , A₂ ,..., A_n называется такая подсистема B₁, B₂ ,...,B_r (каждый из векторов B₁,B₂,...,B_r является одним из векторов A₁ , A₂ ,..., A_n)_, которая удовлетворяет следующим условиям:1. B₁,B₂,...,B_r линейно независимая система векторов;2. любой вектор A_j системы A₁ , A₂ ,..., A_n линейно выражается через векторы B₁,B₂,...,B_r

r — число векторов входящих в базис.

Ранг нулевой матрицы  любых размеров равен нулю

Ранг любого ненулевого вектора-строки (вектора-столбца) равен единице

И вообще – если в матрице произвольных размеров есть хотя бы один ненулевой элемент, то её ранг не меньше единицы

Ранг матрицы по строкам равен рангу матрицы по столбцам.

А чему равен ранг матрицы ? Строки вроде не пропорциональны…, значит, по идее трём. Однако ранг этой матрицы тоже равен двум. Я сложил первые две строки и записал результат внизу, то естьлинейно выразил третью строку через первые две. 

 ранг матрицы не превосходит её минимальной размерности

Определение: ранг матрицы – это максимальное количество линейно независимых строк. Или: ранг матрицы – это максимальное количество линейно независимых столбцов

Базисные столбцы линейнонезависимы и ВСЕ остальные столбцы можно выразить через них

Нахождение базисных столбцов Гауссом: подвести до главной ступенчатой (над единицами на гл диагонали нули)

Столбцы без свободных членов – базисные.

Линейные подпространства могут быть заданы двумя способами: или однородной системой линейных уравненийили линейной оболочной.

Линейное подпространство задано однородной системой линейных уравнений

В задачах в данном случае чаще всего нужно найти размерность и ранг подпространства; или найтифундаментальный набор решений и обозначить базисные и свободные переменные. Отметим некоторые нюансы.

1) Если

{x₁ = x₂ + x₃{x₄ = 2·x₂ − x₃

то x₁, x₄ — базисные переменные, а x₂, x₃ — свободные.

2) Ранг — это количество ненуливых различных строчек, оставшихся в матрице при её решении методом Жордана-Гаусса (метод заключается в том, чтобы в каждом столбце матрицы оставить лишь одну значащую цифру, а все остальные посредством домножения строчек на число и сложения/вычитания обратить в нули)

3) Ранг равен количеству базисных переменных.

4) Размерность — это количество векторов в базисе данного линейного подпространства, максимальное количество линейно-независимых векторов.

5) Размерность равна разности количества переменных и ранга. Это количество свободных переменных.

II) Линейное подпространство задано линейной оболочкой

Линейная оболочка — это набор векторов, которые задают линейное подпространство. Строго говоря, линейная оболочка — это множество всех линейных комбинаций данных векторов. Так же обозначим особенности:

1. Если задана линейная оболочка — ранг набора векторов равен его размерности. С другой стороны в таком случае рангом или размерностью называют минимальное количество линейно независимых векторов в линейном подпространстве.

Задача: найдите ранг, размерность и базис набора векторов а₁ (2,4,1,0,-1), а₂ (1,-1,0,3,2), а₃ (3,9,2,-3,-4), а₄ (-1,7,1,-9,-7)

Решение: Выпишем матрицу и решим её методом Жордана-Гаусса:

Видим, что rank(A) = 2 (строчек две ). Так как дана линейная оболочка, то dim(A) = rank(A) = 2

Итак, в базисе 2 вектора, так как dim(A) = 2. Мы должны выбрать 2 линейно-независимых вектора, которые входят в данное линейное подпространство. Для двух векторов линейная зависимость означает пропорциональность. Значит, выберем 2 непропорциональных вектора. Это, например, а₁ и а₂

Но если в базис бы входило 3 вектора? Пришлось бы опытным путём с помощью матрицы искать 3 линейно независимых.

Множество решений однородной линейной системы относительно n неизвестных является линейным подпространством пространстваRn. Размерность этого подпространства равна n − r, где r − ранг матрицы системы A.

Любой базис пространства решений однородной системы линейных уравнений называется фундаментальной системой решенийоднородной системы.

Иначе говоря, любая упорядоченная совокупность n − r линейно независимых решений однородной линейной системы образуетфундаментальную систему решений однородной системы.

 

Однородная система линейных алгебраических уравнений

с помощью элементарных преобразований может быть приведена к каноническому виду:

 Ранг r матрицы равен 2, число n неизвестных равно 5, система нетривиально совместна. Размерность пространства решений этой однородной системы равна 3: d = n − I = 5 − 2 = 3.

три линейно независимые решения системы

образуют базис пространства решений системы, т.е. образуют её фундаментальную систему решений.

Как найти фундаментальную систему решений линейного уравнения?

Возьмём для примера такую систему линейных уравнений: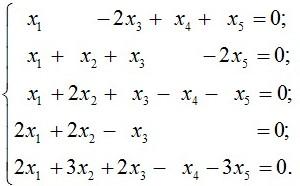Найдём решение этой линейной системы уравнений методом Гаусса. Для начала нам надо выписать матрицу коэффициентов системы.Преобразуем эту матрицу к треугольной. Первую строку переписываем без изменений. И все элементы, что стоят под a11, надо сделать нулями. Что бы сделать ноль в место элемента a21, надо от второй строки вычесть первую, и разность записать во второй строке. Что бы сделать ноль в место элемента a31, надо от третьей строки вычесть первую и разность записать в третьей строке. Что бы сделать ноль в место элемента a41, надо от четвёртой строки вычесть первую умноженную на 2 и разность записать в четвёртой строке. Что бы сделать ноль в место элемента a31, надо от пятой строки вычесть первую умноженную на 2 и разность записать в пятой строке.Первую и вторую строку переписываем без изменений. И все элементы, что стоят под a22, надо сделать нулями. Что бы сделать ноль в место элемента a32, надо от третьей строки вычесть вторую умноженную на 2 и разность записать в третьей строке. Что бы сделать ноль в место элемента a42, надо от четвёртой строки вычесть вторую умноженную на 2 и разность записать в четвёртой строке. Что бы сделать ноль в место элемента a52, надо от пятой строки вычесть вторую умноженную на 3 и разность записать в пятой строке.Видим, что последние три строки – одинаковые, поэтому если от четвёртой и пятой вычесть третью, то они станут нулевыми.По этой матрице записываем новую систему уравнений.Видим, что линейно независимых уравнений у нас, только три, а неизвестных пять, поэтому фундаментальная система решений будет состоять из двух векторов. Значит, нам надо перенести две последние неизвестные вправо.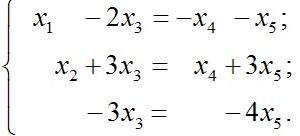Теперь, начинаем выражать те неизвестные, что стоят в левой части через те, что стоят в правой части. Начинаем с последнего уравнения, сначала выразим x3, потом полученный результат подставим во второе уравнение и выразим x2, а потом в первое уравнение и тут выразим x1. 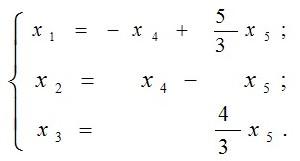Таким образом мы все неизвестные, что стоят в левой части, выразили через неизвестные, что стоят в правой части.После чего вы вместо x4 и x5, можем подставлять любые числа и находить x1, x2 и x3. Каждая такая пятёрка чисел будет корнями нашей изначальной системы уравнений. Что бы найти векторы, что входят вФСР нам надо вместо x4 подставить 1, а вместо x5 подставить 0, найти x1, x2 и x3, а потом наоборот x4=0 и x5=1.