быстрый линальчик
.pdf
Вопрос1!
Доказать, что линейная оболочка системы векторов является подпространством. Нахождение размерности подпространства.
Вопрос2!
Доказать, что множество всех решений однородной системы линейных уравнений с n
неизвестными образует подпространство в R^n.
Вопрос3!
Определить понятие единичного базиса в Rn
Вопрос4!
4 Определить сумму и пересечение подпространств
Пусть и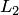
— подпространства линейного пространства.
Пересечением подпространств 
и
называетсямножество векторов, каждый из которых принадлежитодновременно, т.е. пересечение подпрос определяется как обычное пересечение двух множеств.
Алгебраической суммой подпространств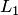 
и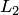
называется множество векторо вида , где . Алгебраическая сумма (короче просто сум подпространств обозначается
1.Пересечение подпространств является подпространством. Поэтому размерности, базиса и т.п. применяются к пересечениям.
2.Сумма подпространств является подпространством.Поэтому понятия размерност базиса и т.п. применяются к суммам.
Теорема о размерности суммы подпространств. Есл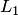и 
и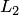 
подпространства конечномерного линейного
пространства 
, то размерность суммы подпространств равна сумме их размерностей без размерности их пересечения (формула Грассмана):
Вопрос5!
Доказать, что сумма подпространств и пересечение подпространств есть подпространство.
Если M1 и M2 — подпростанства простанства V, то M1 + M2 и M1 M2 также являтся подпростанствами в V.
Доказательство. В силу замечания о нулевом векторе и подпростанствах каждое из подпростанств M1 и M2 содержит нулевой вектор. Следовательно, 0 = 0 + 0 M1 + M2 и 0 M1 M2. В частности, множества M1 + M2 и M1 M2 — непустые. Далее, пусть x, y M1 + M2 и t — произвольный скаляр.
Тогда x = x1 + x2 и y = y1 + y2, для некоторых x1, y1 M1 и x2, y2 M2. Учитывая, что M1
иM2 — подпростанства, получаем, что
x+ y = (x1 + x2) + (y1 + y2) = (x1 + y1) + (x2 + y2) M1 + M2, tx = t(x1 + x2) = tx1 + tx2 M1 +
M2.
Следовательно, M1 + M2 — подпростанство в V. Далее, пусть x, y M1 M2 и t — произвольный скаляр. Тогда x, y M1 и x, y M2. Поскольку M1 и M2 — подпростанства, имеем x + y M1, x + y M2, tx M1 и tx M2. Следовательно, x + y M1 M2 и tx M1 M2, и потому M1 M2 — подпростанство в V.
Вопрос6!
Вопрос7!
Доказать теорему о единственном представлении произвольного вектора в виде суммы векторов, принадлежащих данному подпространству и его прямому дополнению.
Вопрос8!
Дать определения сюръективного, инъективного и биективного отображения. Обратное отображение.
Вопрос9!
Дать определение линейного оператора. Привести примеры
Вопрос10!
Определить матрицу линейного оператора в данном базисе. Привести примеры
Вопрос11!
Вывести формулу для нахождения образа вектора в данном базисе при заданной матрице оператора.
Вопрос12!
Дать определения образа и ядра оператора. Привести примеры.
Вопрос13!
Ядро и образ линейного оператора являются линейными подпространствами V, т.е. подмножествами, замкнутыми относительно линейных операций в пространстве.
Вопрос14!
Доказать необходимые и достаточные условия для матрицы, ядра и образа биективного оператора.
-r = n, матрица невырождена
-Ядро – вектор 0
-Образ - Rn
-Взаимно-однозначное соответствие
Вопрос15!
Вывести формулу приобразования матрицы линейного оператора при переходе к другому базису.
Вопрос16!
Разбиение множества матриц одного порядка на классы подобных матриц. Неизменность величины определителя матрицы и величины следа матрицы в каждом классе подобных матриц.
Матрицы в классах подобных матрицах имеют один и тот же характеристический многочлен. Так как он представляется в виде x2 – Tr(A)*x + Det(A) = 0. Отсюда равенство Det(A) и Tr(A) для всех всех матриц.
Вопрос17!
Определить действия с линейными операторами.
Вопрос18!
Произведение линейного оператора. Матрица произведения линейного оператора.
Произведением линейных операторов А и В из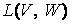 
называется оператор АВ, определяемый следующим образом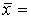: (А В)
А(В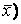
для любого 
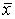из V. Произведение линейных операторов тоже будет линейным оператором.
Справедливы следующие свойства умножения линейных операторов:
1.
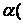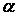А В ) = (
А )В.
2.(А В ) Е = А (В Е ).
3. (А + В)Е = А Е + В Е , Е ( А + В) = Е А + Е В .
Вопрос19!
Условия существования обратного оператора. Матрица обратного оператора.
Вопрос20!
Дать определение собственного вектора и собственного значения линейного оператора. Привести примеры. Свойства собственных векторов данного оператора.
Вопрос21!
Доказать линейную независимость системы собственных векторов оператора , имеющих различные собственные значения.
Вопрос22!
Изложить процесс нахождения собственных векторов и собственных значений линейного оператора.