57. Дать определение по Гейне и по Коши: существует :

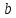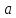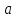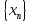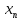Определение левого предела по Гейне: Число называется левым пределом функции в точке , если для любой сходящейся к последовательности , элементы которой меньше , соответствующая последовательность 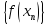сходится к .

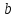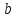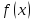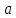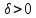Определение левого предела по Коши. Число называется левым пределом функции в точке , если для любого существует такое, что для всех , удовлетворяющих неравенствам 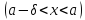выполняется неравенство .

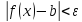65. Дать определения по Гейне и по Коши: существует

По Гейне: число b называется приделом функции f(x) при х→∞ если для любой бесконечно большой последовательности {Xn} значение аргумента соответствует числовой последовательности {f(Xn)} сходится к числи b

По Коши: число b называется приделом функции f(x) при х→∞ если для любого ε>0 существует δ>0 такое что для всех значений аргумента, для которых lxl>δ выполняется равенство lf(x)-bl<ε

66. Дать определения по Гейне и по Коши: существует

По Гейне: число b называется приделом функции f(x) при х→+∞ если для любой бесконечно большой последовательности значений аргумента Xn элементы которой больше нуля Xn>0 соответствует числовой последовательности {f(Xn)} сходится к числи b

По Коши: число b называется приделом функции f(x) при х→+∞ если для любого ε>0 существует δ>0 такое что для всех x, удовлетворяющих неравенство x>δ выполняется равенство lf(x)-bl<ε

67. Дать определения по Гейне и по Коши: существует

По Гейне: число b называется приделом функции f(x) при х→-∞ если для любой бесконечно большой последовательности значений аргумента {Xn} элементы которой больше нуля Xn<0 соответствует числовой последовательности {f(Xn)} сходится к числи b

По Коши: число b называется приделом функции f(x) при х→-∞ если для любого ε>0 существует δ>0 такое что для всех x, удовлетворяющих неравенство x<-δ выполняется равенство lf(x)-bl<ε

78. Первый замечательный придел.

.

79. Второй замечательный придел.

.

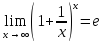80.Четвёртый замечательный предел.

.

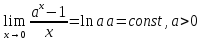81.Пятый замечательный предел.

.

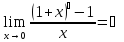82. Третий замечательный предел.

.

83. .

84. = 0

85.=

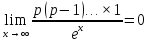
86. Определение функции, непрерывной в точке а: Функция 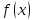называется непрерывной в точке 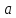, если в этой точке существует предел функции и этот предел равен

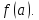
87. Определение функции, непрерывной в точке а справа(слева): Функция называется непрерывной в точке 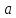справа(слева), если в этой точке существует предел функции справа (слева) и этот предел равен

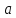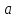88. Определение точки устранимого разрыва функции: Точка называется точкой устранимого разрыва функции , если в точке существуют равные односторонние пределы, но эти пределы не равны значению функции в точк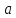е , т.е.

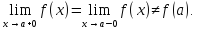
89. Определение точки разрыва функции 1 рода: Точка называется точкой разрыва первого рода функции 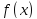, если в этой точке существуют не равные конечные односторонние пределы, т.е.

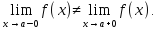
90.Сформулировать теорему о непрерывности сложной ф-ции.

Любой многочлен является непрерывной функцией в любой точке вещественной прямой, а любая дробно-рациональная функция непрерывна в каждой точке, в которой знаменатель дробно-рациональной функции не равен нулю.

Теорема: пусть ф-ция (х) непрерывна в т. х_0, а ф-ция Z= f(y) непрерывна в т. у, где у₀=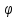 (х₀), тогда ф-ция f[ (х₀)] непрерывна в т. х₀

91.Определение точки разрыва ф-ции 2го рода.

Т. а называется точкой разрыва ф-ции f(x), если в этой точке ф-ция не является непрерывной.

Т. а называется точкой разрыва 1-го рода, если в этой точке существуют неравные конечные односторонние пределы.

Т. а называется точкой разрыва 2-го рода, если хотя бы один из двух односторонних пределов либо не существует, либо является бесконечным.

92. Сформулировать первую теорему Вейерштрасса.

Пусть ф-ция f(x) непрерывна на сегменте [а,в], тогда эта ф-ция ограничена на сегменте [а,в].

93. Сформулировать вторую теорему Вейерштрасса.

Если ф-ция f(x) непрерывна на сегменте [а,в], то она достигает на этом сегменте своих точных граней,т.е. существуют такие точки х₁ и х₂ сегмента [а,в], что sup_[а,в]f(x)= f(x₁); inf _[а,в]f(x)= f(x₂)

94. Теорема о прохождении непрерывной ф-ции через нуль при смене знаков.

Пусть ф-ция f(x) непрерывна на сегменте [а,в], f(а) и f(в) имеют разные знаки.

Существует с принадлежащая [а,в] f(а)=0(в которой значение аргумента=0)

95. Теорема о постоянстве знака непрерывной функции.

Пусть f(x) непрерывна в т. А и f(а)≠0, тога существует δ-окрестность в lim которой f(x) имеет знак = f(а)

96. Определение обратной функции.

Пусть на множестве х задана ф-ция у= f(x), через У обозначим мн-во значений этой ф-ции.Предположим, что для каждого значения у принадл. У можно поставить в соответствие элемент х принадл. Х такой, что f(x)=у следовательно можно говорить о некоторой ф-ции с областью определенияУ областью значений Х.Эту ф-цию будем называть обратной ф-цией f(x) х= f^-‘(у)

97. Теорема о существовании и непрерывности обратной ф-ции.

Пусть ф-ция у= f(x) непрерывна и возрастает (убывает) на сегменте [а,в] при этом f(а)=α, а f(в)=β, тогда на сегменте [α,β]( на сегменте [β,α]) существует обратная к ф-ции f(x), которая непрерывна и возрастает(убывает) на сегменте [α,β]( [β,α])

98. Определение дифференцируемой ф-ции.

Пусть ф-ция f(x) определена на (а,в) и пусть х-некоторая точка принадлеж. (а,в)

ф-ция f(x) называется фифференцируемой в точкех, если ее приращение в этой точке можно представить в виде Δу= f(x+Δх)- f(x)=А Δх+α(Δх) Δх, где А – это постоянная, не зависящая от Δх, а α(Δх) явл бесконечно малой ф-цией при Δх→0

99. Определение производной ф-ции.

Если существует конечный предел разностного отношения при Δх→0, то этот предел называется производной ф-ци f(x) в точке х. Заметим, что если производная существует в каждой точке интервала (а,в), то эта произв сама является ф-цией, определенной на этом интервале.

100.Первый дифференциал ф-ции.

Dy=(x)dx

101. Теорема о производной суммы, разности, произведения и частного двух ф-ций.

Если ф-ция U(x) и V(x) диф-емы в некот. Т. х , то сумма, разность, произведение и частное этих ф-ций(в случ частного V(x)≠0 в т. х ).Диф-мой в т. х и при этом справ нер-ва [U(x) ±V(x)]’=U’(x)± V’(x); [U(x)V(x) ]’= U’(x) V(x)+ V’(x) U(x);(ну и частное писать долго(()

102. Теорема о производной сложной ф-ции.

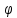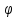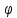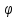Если х= (t) диференц в некоторой т. t, а у= f(x) диф-ма в т. (t), то f[ (t)] – диф-ма в т. t и при этом справ. Нер-во {f[ (t)]}’= f’[ (t)] ’(t)

103. Теорема о производной обратной ф-ции.

Пусть ф-ция у= f(x) непрерывна и монотонна в некоторой окрестн т. х кроме того пусть ф-ция f(x) диф-ма в т. х и ее f¹(x) в данной точке ≠0, тогда в окрестности т. f(x) определена обратная ф-ция х= f¹(у), которая монотонна, непрерывна и диф-ма в т. f(x)

104. Формула Лейбница для производной порядка n для произведения двух ф-ций.

[U(x)V(x) ]⁽ⁿ⁾=c^k_nU^(n-k)(x)V^(k)(x)

105. Таблица производных элементарных ф-ций.

1.(х^α)’=α х^α-1 2.(а^х)’= а^хln а 3.(log_аx)’=1/xlnа 4.(sinx)’=cosx 5.(cosx)’=-sinx 6.(tgx)’=1/cos²x 7.(ctgx)’=-1/sin²x 8.(arcsinx)’=1/(1-x²)^1/2 9.(arccsx)’=-1/(1-x²)^1/2 10.(arctgx)’=1/(1-x²) 11. (arcctgx)’=-1/(1-x²)

106. Сформулировать в виде теоремы свойство инвариантности формы первого дифференциала.

dy= f^-‘(x) универсальная формула

Справедлива в случае не только когда аргум х является независимой переменной, но и в случае, когда арг х представл собой диф-мую ф-цию от t

107. Дать определение точки локального максимума ф-ции y=f(x) и критической точки ф-ции y=f(x).

Т. х области опред ф-ции у= f(x) называется точкой локального максим.(минимума) если существует такая окрестность т х₀, что для любого х из указанной окрестности справ.нер-во f(x)≤ f(x₀)( f(x)≥ f(x₀)). Если х₀ явл точкой лок макс(мин), то наз-ся точкой лок экстремума

108.поебень.

Если ф-ция f(x) диф-ма в т х₀ и в этой точке имеет лок экстремум, то произв в т х₀=0

114. Теорема Ролля.

Пусть ф-ция f(x) непрерывна на сегменте [а,в] и диф-ма на инт (а,в) кроме этого пусть f(а)=f(в), тогда существует такая т ξ принадл (а,в), f^-‘(ξ)=0

115. Теорема Лагранжа.

Пусть ф-ция f(x) непрерывна на сегменте [а,в] и диф-ма на инт (а,в) тогда существует такая т ξ принадл (а,в), что справ нер-во f(а)-f(в)= f^-‘(ξ)( в- а)

116. Теорема Коши.

Пусть ф-ции f(x) и g(x) непрерывны на сегменте [а,в] и диф-мы на инт (а,в), кроме этого g’(x)≠0 в кажд точке х принадл (а,в), тогда существ такая т ξ принадл (а,в),что справ нер-во (f(а)-f(в))/(g(b)-g(a))=f’(ξ)/g’(ξ)

117. 1-е правило Лопиталя.

Пусть ф-ции f(x) и g(x) диф-мы в некот окрестности т а , за исключение быть может самой т а. Пусть пределы f(x) = g(x) существуют и равны0 и g’(x)≠0 всюду в указанной окр а, тогда если существует конечный или бесконечный 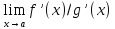, то и существ и при этом они равны(пределы)

118. 2-е правило Лопиталя.

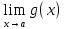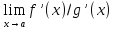Если ф-ции f(x) и g(x) диф-мы в некот окрестности т а , за исключение быть может самой т а. и равны и кроме этого g’(x)≠0 в указанной окр а, тогда если существует , то и существ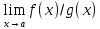 и при этом они равны(пределы).