Лекція № 18
Тема: Лінійні неоднорідні системи
Диференціальних рівнянь. Знаходження
часткових розв’язків лінійної неоднорідної
системи диференціальних рівнянь методом
Лагранжа.
Розглянемо лінійну неоднорідну систему диференціальних рівнянь:
(1)
Теорема: Якщо відомо загальний розв’язок відповідної однорідної системи, то розв’язування неоднорідної системи зводиться до квадратур.
Доведення:
Нехай
-
загальний розв’язок відповідної
лінійної однорідної системи диференціальних
рівнянь. Введемо нові функції
так, щоб:
були
розв’язками неоднорідної системи
рівнянь. Підставимо ці функції в систему:
Провівши аналогічні міркування
для 2-го, 3-го, ... , n-го
рівнянь робимо висновок, що
є частковим розв’язком системи (1).
Нехай нам відомо загальний розв’язок відповідної однорідної системи для (1):
Частковий розв’язок
неоднорідної системи шукатимемо у
вигляді загального розв’язку відповідної
однорідної системи вважаючи
функціями від х.
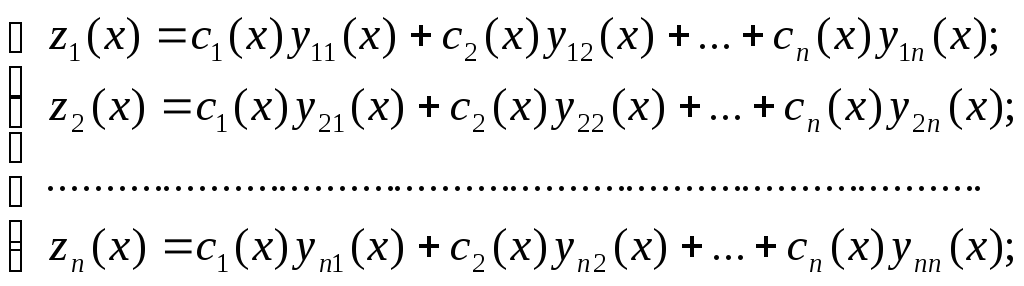
Підставимо
в
перше рівняння системи (1):
Перегрупуємо:
Виконавши аналогічні дії що до 2-го, 3-го, і n-го рівнянь матимемо:
Отримали лінійну неоднорідну
алгебраїчну систему рівнянь відносно
Визначник основної матриці буде:
За Кантором має і при тому єдиний
розв’язок.
Тоді:
Для визначення
отримали звичайне диференціальне
рівняння
порядку.
Тоді:
Приклад:
Розв’язати систему диференціальних рівнянь:
Знайдемо розв’язок відповідної однорідної системи:
Підставимо функції в систему:
Маємо:
Тоді:
