Формула Ліувіля-Остроградського

Нехай n- лінійно-незалежних частинних розв’язків рівняння (2). Тоді це рівняння можна представити у вигляді:

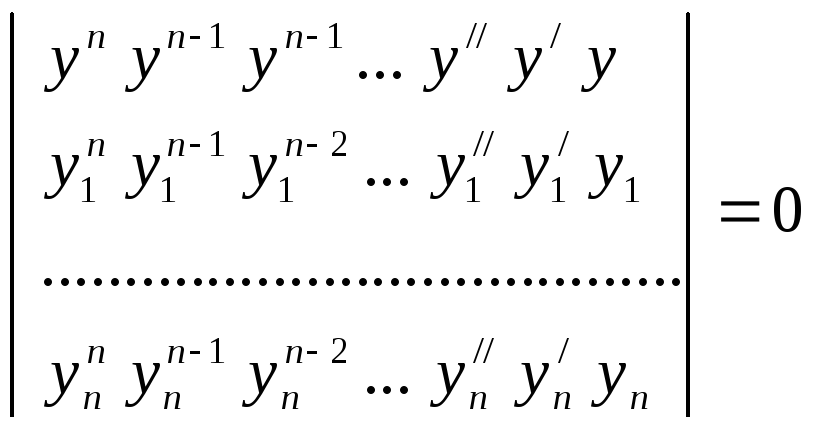(4)

Дійсно рівняння (4) еквівалентне рівнянню (2). Оскільки підставивши в нього довільний розв’язок рівняння (1) отримаємо в лівій частині (4) визначник, що має 2 однакових рядки. Розкладемо ліву частину рівняння (4) за елементами першого рядка. Отримаємо:

Тоді рівняння (4) врахувавши, що - (визначник Вронського),

.

Оскільки це рівняння тотожне рівнянню (2), то прирівнюючи коефіцієнти при однакових похідних матимемо:

; , ... , , ... , ;

Знайдемо залежність від W.

Озн. Похідною визначника n-ого порядку зветься сума n визначників n-ого порядку перший рядок (стовпець) першого визначника є похідні елементів першого рядка, інші без змін і.т.д., n-ий рядок (стовпець) n-ого визначника складається з похідних елементів цього рядка, а інші без змін. Візьмемо похідну від W по х:

Отже , . Вважаючи функцію заданою, а Вронський W невідомий то інтеграл рівняння відносно W дістанемо:

(5),

де с – довільна стала. Якщо задати початкову умову , то матимемо:

(6).

Формули (5) і (6) дають змогу знаходити визначник Вронського фундаментальної системи розв’язків рівняння (2) не маючи ще цієї системи, звуть формулами Ліувіля-Остроградського.

Приклад:

Знайти диференціальне рівняння, для якого функції , скл. ФСР (фундаментальна система розв’язку).

Розв’язок:

Використаємо (4):

; ,

- шукане диференціальне рівняння.

Загальним розв’язком неоднорідного рівняння (1) є сума будь-якого його частинного розв’язку a(x) і загального розв’язку U(x) однорідного рівняння (2):

; або y(x) = U(x) + V(x),

Дійсно:

Теорема 4:

Частинний розв’язок V(x) рівняння: (7) можна подати у вигляді суми:

, де - відповідно розв’язки рівнянь ;

Доведення:

Дійсно , . Додавши отримаємо:

.

Отже сума є розв’язком рівняння (7).

Властивість суперпозиції розв’язків:

Якщо функції є розв’язками рівняння , , тобто , то функція , - const є розв’язком рівняння .

Теорема 5:

Якщо диференціальне рівняння (2) має розв’язок виду U(x) + V(x), то кожна з функцій U(x) і V(x) є розв’язком диференціального рівняння (7).

Доведення:

Дійсно за адитивною властивістю оператора маємо:

.

Звідси слідує, що L [ U(x) ] = 0, L [ V(x)] = 0.

Якщо рівняння L [y] = e(x) і (x), де всі - дійсний має розв’язок , то дійсна частина U(x) і уявна V(x) є відповідно розв’язками рівнянь

L [y] = f(x) і L [y] = (x).

(Доведемо аналогічно до попереднього випадку).

Лекція № 12

Тема: Метод варіації довільної сталої (Лагранжа).

Розв’язування неоднорідних лінійних

диференціальних рівнянь n-го порядку.

Відомо див. лекцію 10-11 що загальний розв’язок неоднорідного рівняння (1) (Л. 10-11), завжди можна знайти якщо відомо загальний розв’язок рівняння (2) (Л. 10-11) і будь-який частинний розв’язок рівняння (1) (Л. 10-11).

Для знаходження частинних розв’язків неоднорідного рівняння існує метод варіації довільної сталої. Ще його наз. метод Лагранжа.

Нехай маємо загальний інтеграл рівняння (2) (Л. 10-11).

(1) де - довільні дійсні сталі.

Частинний розв’язок рівняння (1) шукаємо у вигляді (1) вважаючи, що - є довільні функції від x ( їх нам потрібно конкретно знайти ).

. Диференціюємо по x дане рівняння:

.

Вважаємо, що має виконуватись:

Тоді:

Диференціюємо отриманий вираз по x.

Знову вважатимемо такими, що

Тоді:

Підставивши отримані значення похідних невідомої функції у рівняння (1) (Л. 10-11) і зробивши елементарні алгебраїчні перетворення. Матимемо:

Як бачимо вирази при тотожно рівні нулю, оскільки є лінійно-незалежними розв’язками рівняння (1) (Л. 10-11). Отже функції повинні одночасно задовольняти записані вище умови. Тобто маємо систему:

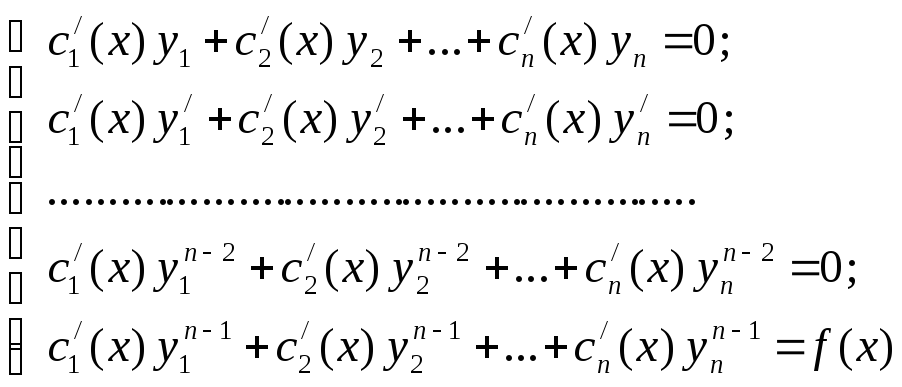
Отримали систему n лінійних рівнянь з n-невідомими. Оскільки визначник даної системи є визначником Вронського для функцій , а ці функції є лінійно-незалежні, то він не рівний нулю, а отже наша система має єдиний розв’язок.

Розв’язавши систему матимемо:

Знайдемо невідомі коефіцієнти , тоді:

, де - довільні сталі.

Тоді частковий розв’язок рівняння (1) (Л. 10-11), матиме вигляд:

Тепер ми можемо записати загальний розв’язок рівняння (1):

Приклад:

Знайти загальний розв’язок рівняння ( використати метод варіації довільної сталої ). Складемо відповідне однорідне рівняння.