Аналитическое выражение поля δт:

Под ΔТ понимается приращение модуля полного вектора напряжённости магнитного поля, т.е. разность между реально существующим значением поля Т и его теоретически ожидаемым, нормальным значением Т_о в данной точке.,

- магнитный азимут составляющей Н_аном (угол между Н_а и Н_о).

(Т_а/Т_о)² → мала.

- наклонение вектора Т_о;

- угол между векторами Т_о и Н_а, который определяется

.

Так как Т_а << Т_о, то и

, - справедливо для тел любой формы.

На северном полюсе, где .

На южном .

На магнитном экваторе .

, т.е. на магнитном экваторе при любом напр-ии : .

Если , то территория высоких широт (магнитные бури, северное сияние).

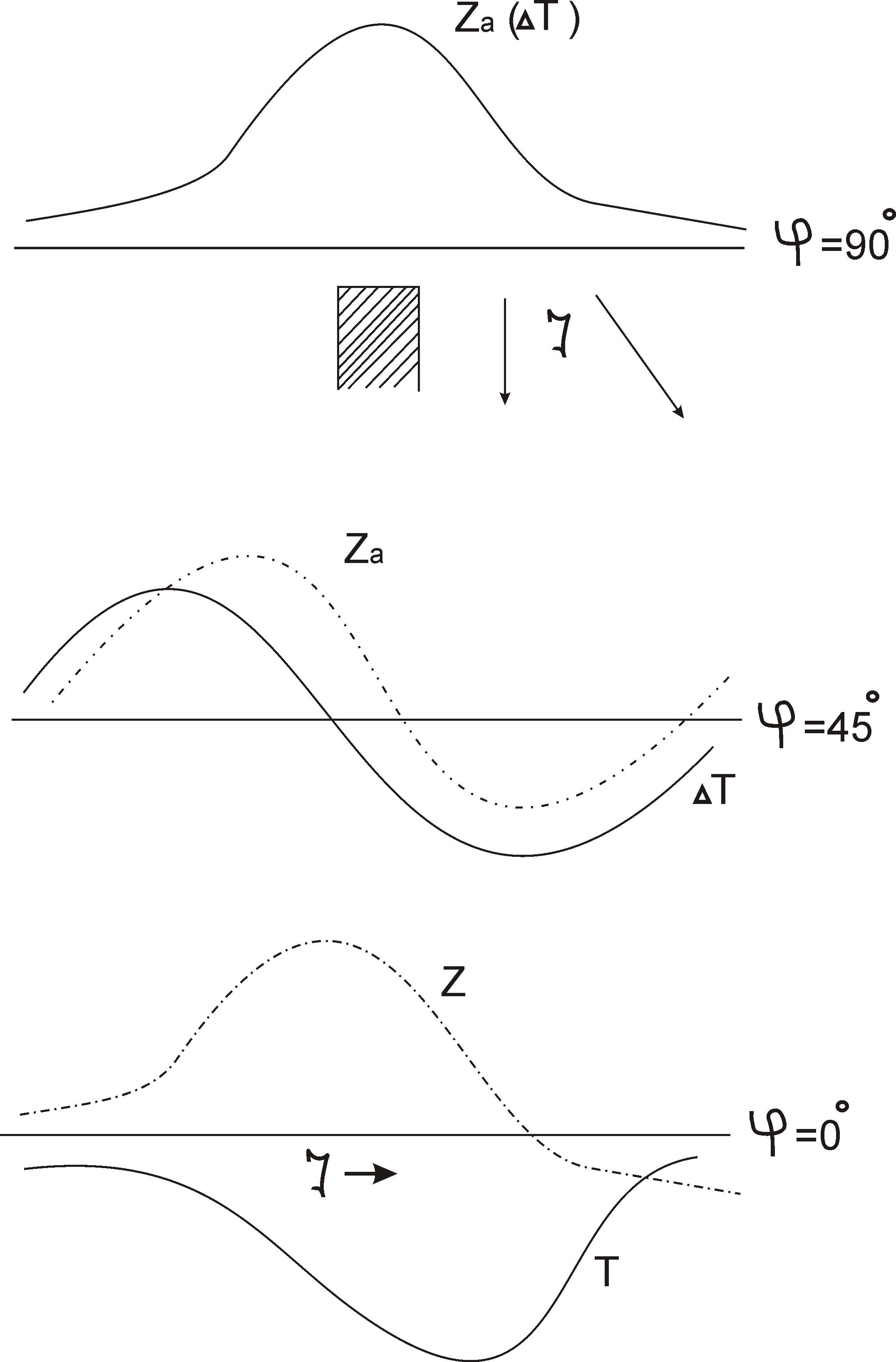
Аномалии ΔТ и вертикального пласта, намагниченного современным земным магнитным полем в различных магнитных широтах.

Общее аналитическое выражения составляющих напряжённости магнитного поля намагниченных тел

Магнитный потенциал элементарного диполя

,

- магнитный момент диполя;

- расстояние от центра диполя до точки, в которой определяется её потенциал.

- угол между напряжением и .

Потенциал магнитного тела, занимающего объём при :

, (1)

,

где , , ,

, , - проекции на соответствующие оси.

- аналитическое выражение потенциала.

Если совпадает с одной из координатных осей, то

,

-

составляющие напряженности магнитного поля есть частные производные магнитного потенциала по соответствующим направлениям, взятые с обратным знаком.

(2)

(2)

Составляющие напряжения магнитного поля при , совпадающей по направлению с одной из координатных осей, приводятся к виду:

(3)

В этих выражениях дифференцирование выполняется по координатам точки наблюдения (х; у; z), а интегрирование по координатам тела , поэтому дифференцирование может быть проведено под знаком интеграла, учитывая, что

,

Из этих выражений следует, что

. (5)

Подставив (4) в (2) получаем соотношение, связывающее составляющие напряженности магнитного поля при намагниченности произвольного направления и при ориентировании по осям прямоугольной системы координат.

(6)

С учётом (5):

(7)

Обозначим через i наклонение вектора , то есть угол между вектором и её проекцией на плоскость ХОУ.

А – угол между проекциями вектора на ось Х и на плоскость ХОУ.

Пространственное положение вектора намагниченности:

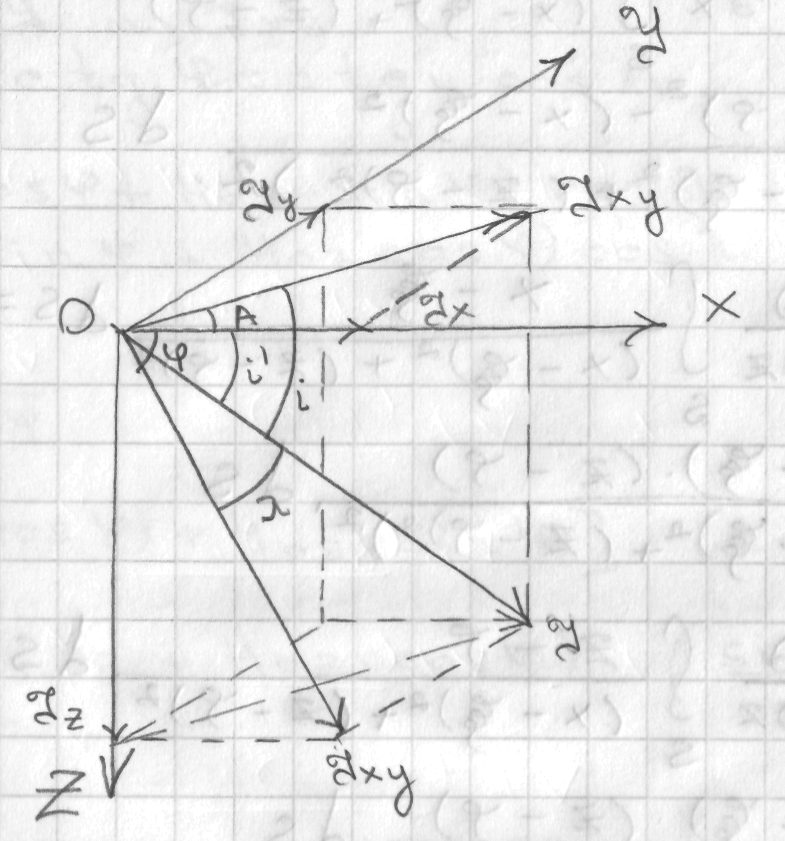
(8)

С учётом (5):

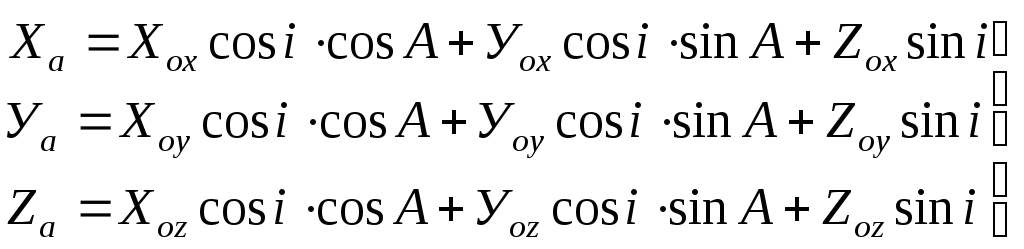(9)

Рассмотрим случай, когда тело считаем вытянутым бесконечно по оси У. При этом условии магнитный потенциал с изменением У остаётся постоянным и его производные по этой переменной равны нулю.

На основании формулы (3) имеем:

,

S - площадь сечения тела плоскостью XOZ;

- элемент площадки;

- элемент длины вдоль оси У.

(10)

Если тела бесконечны по простиранию, то .

С учетом (8) и (9):

(11)

Удобнее пользоваться, когда коэффициентами при и будут функции угла, лежащего в плоскости ХОZ . Обозначим через угол между проекциями на плоскость ХОZ () и осью Х.

- угол между У и .

Тогда , и

(12)

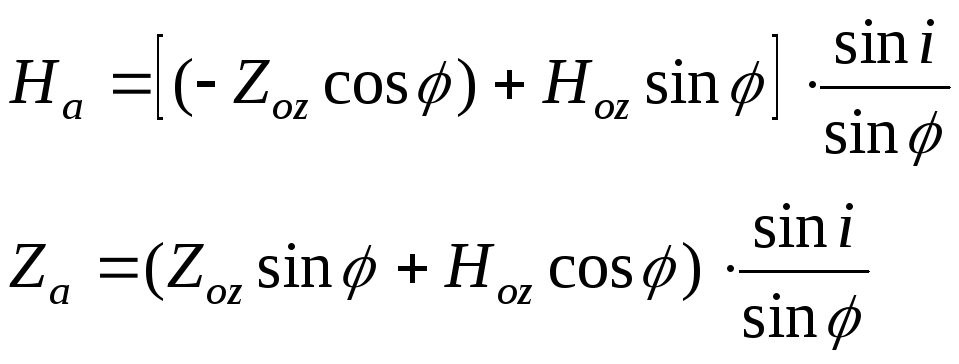
В случае, если известен угол падения г.п. (при условии, что он отсчитывается от «+» направления оси Х и тело намагничено так, что вектор намагниченности лежит в плоскости падения), то

, где

Z_n, H_n - соответственно вертикальная и горизонтальная составляющие над пластом.

На основании теоремы Гаусса

,

S- замкнутая поверхность, ограничивающая объем;

J_n - проекция вектора намагниченности на внешнюю нормаль к элементу поверхности dS.

Вывод: магнитные аномалии созданы только поверхностными, а не объёмными распределениями источников поля, поэтому условно можно считать, что плоские границы тела, параллельные , магнитного поля не создают и что знаки магнетизма на двух параллельных плоскостях тела противоположны. Эти допущения часто применяют при количественных расчётах.

\Лекция №