Пример 3

Задается: схема нагружения балки (рис. 14), длины участков балки: 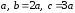, распределенная нагрузка интенсивностью , величина сосредоточенной силы , величина изгибающего момента .

Требуется: построить эпюры перерезывающей силы и изгибающего момента при известной нагрузке и схеме нагружения балки.

Рис. 14. Схема нагружения балки.

1. Определение опорных реакций (рис. 14).

Для определения опорных реакций составляются уравнения равновесия балки:

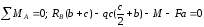, откуда .

, откуда .

Проверка: .

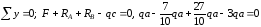2. Разбивка балки на участки.

2. Для построения эпюры перерезывающей силы и изгибающего момента необходимо рассмотреть три участка с координатами и (рис. 14).

3. Определение законов изменения перерезывающей силы 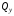и изгибающего момента по участкам балки. Начало рассматриваемых участков необходимо обозначать точкой, текущее значение стрелкой. Начало последующего участка начинается на границе предыдущего участка.

1. Первый участок (рис. 15).

Рис. 15. К определению 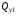и на первом участке.

Координата для первого участка изменяется в пределах . Уравнения равновесия для отсеченной (левой) части балки имеют вид:

.

На первом участке перерезывающая сила постоянна по длине участка .

.

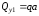Изгибающий момент на границах участка принимает значения:

при , при .

2. Второй участок (рис. 16).

Рис. 16. К определению и на втором участке.

Координата для второго участка изменяется в пределах . Уравнения равновесия для отсеченной (левой) части балки имеют вид:

.

На втором участке перерезывающая сила постоянна по длине участка и равна .

.

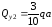Изгибающий момент на границах участка принимает значения:

при ,

при .

3.3. Третий участок (рис. 17).

Рис. 17. К определению и на третьем участке.

Координата для третьего участка изменяется в пределах . Уравнения равновесия для отсеченной (правой) части балки имеют вид:

.

Перерезывающая сила на границах участка принимает значения:

при ,

при .

.

Изгибающий момент на границах участка принимает значения:

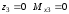при , при .

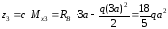В координатах M_x3-z₃ полученное выражение изгибающего момента M_x3 описывает кривую второго порядка. Определим выпуклость кривой:

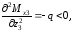следовательно кривая выпукла вверх.

Условие экстремума кривой , следовательно, функция 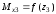имеет экстремум при .

Вычислим величину изгибающего момента при :

.

По результатам вычислений строятся эпюры поперечной (перерезывающей) силы и изгибающего момента (рис. 18).

4. Выполняем проверку правильности построения эпюр и .

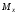   1. На участке СВ, где действует распределенная нагрузка q:

• эпюра - наклонная прямая;

• эпюра - кривая второго порядка;

• в сечении =0, а изгибающий момент принимает экстремальное значение .

2. В сечениях К, А, С и В, где приложены сосредоточенные силы на эпюре имеют место «скачки» на величину приложенных сил.

3. В сечении К, где приложен сосредоточенный момент на эпюре 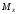имеет место «скачок» на величину данного момента.

4. На участках балки, где положительна эпюра 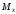возрастает.

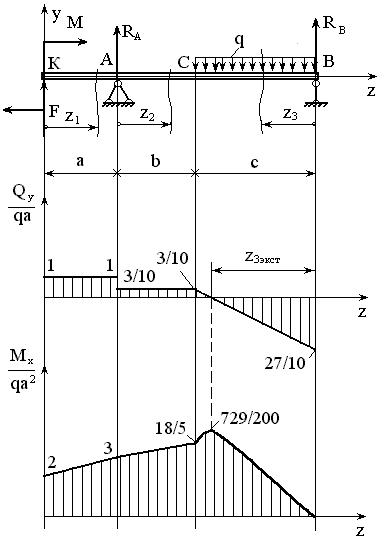
Рис. 18. Расчетная схема бруса, эпюры поперечной силы 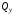и изгибающего момента .