Плоскости частного положения

а. Проецирующие плоскости Плоскость, перпендикулярная одной из плоскостей проекций, называется проецирующей. Горизонтально проецирующая плоскость - плоскость, перпендикулярная П₁ (рис. 2.3.4). Р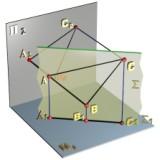ис. 2.3.4

Горизонтальная проекция плоскости вырождается в прямую линию ₁, положение которой соответствует положению плоскости в пространстве (₁ = П₁). Фронтальная проекция плоскости представляет собой множество точек, совпадающее с множеством точек плоскости П₂ (₂ = П₂). Горизонтальная проекция любой геометрической фигуры, принадлежащей плоскости , например треугольника АВС, совпадает с горизонтальной проекцией ₁ плоскости . Показанные на рис. 2.3.4 углы и - величины углов наклона плоскости соответственно к фронтальной и профильной плоскостям проекций.

Фронтально проецируюшая плоскость - плоскость, перпендикулярная П₂ (рис. 2.3.5). Фронтальная проекция такой плоскости вырождается в прямую линию ₂, положение которой соответствует положению плоскости в пространстве (₂ = П₂). Горизонтальная проекция представляет собой множество точек, совпадающих с множеством точек плоскости П₁ (₁ = П₁). Р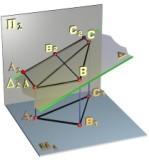ис. 2.3.5

Фронтальная проекция любой геометрической фигуры, принадлежащей плоскости , например треугольника ABC, совпадает с фронтальной проекцией ₂ плоскости . Показанные на рис. 2.3.5,б углы и - величины углов наклона плоскости к горизонтальной и профильной плоскостям проекций. Профильно проецирующая плоскость - плоскость, перпендикулярная П₃, (рис. 2.3.6). Профильная проекция плоскости вырождается в прямую ₃, положение которой соответствует положению плоскости в пространстве (₃ = П₃). Горизонтальная и фронтальная проекции представляют собой множество точек, совпадающих соответственно с множеством точек плоскостей П₁ и П₂. Р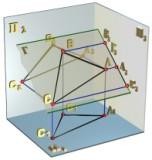ис 2.3.6.

Профильная проекция любой геометрической фигуры, принадлежащей плоскости Г, например треугольника АВС, совпадает с профильной проекцией Г₃ плоскости Г. Показанные на рис. 2.3.6 углы и - величины углов наклона плоскости Г к горизонтальной и фронтальной плоскостям проекций.

6. Плоскости уровня

Плоскость, параллельная одной из плоскостей проекций, называется плоскостью уровня. Горизонтальная плоскость уровня - плоскость, параллельная П₁ (рис. 2.3.7). Р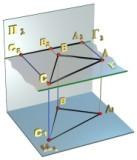ис 2.3.7

Горизонтальная плоскость уровня Г перпендикулярна плоскостям П₂ и П₃ т. е. является фронтально и профильно проецирующей одновременно и обладает, следовательно, свойствами каждой из них. Любая геометрическая фигура Ф, принадлежащая плоскости Г (рис. 2.3.7), проецируется на горизонтальную плоскость проекций в конгруэнтную ей фигуру Ф₁, например:

ABC A₁B₁C₁ ABC

Фронтальная плоскость уровня - плоскость, параллельная П₂ (рис. 2.3.8). Р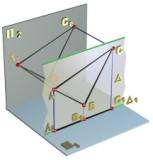ис 2.3.8

Фронтальная плоскость уровня перпендикулярна плоскостям П₁ и П₃ т. е. является горизонтально и профильно проецирующей одновременно и обладает, следовательно, свойствами каждой из них. Любая геометрическая фигура Ф, принадлежащая плоскости , проецируется на фронтальную плоскость проекций в конгруэнтную ей фигуру Ф₂, например;

ABC A₂B₂C₂ ABC

Профильная плоскость уровня - плоскость, параллельная П₃ (рис. 2.3.9). Р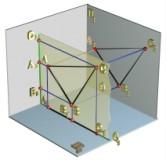ис 2.3.9

Профильная плоскость уровня перпендикулярна плоскостям П₂, и П₁, т. е. является горизонтально и фронтально проецирующей одновременно и обладает, следовательно, свойствами каждой из них. Любая фигура Ф, принадлежащая плоскости , проецируется на профильную плоскость проекций в конгруэнтную ей фигуру Ф₃, например:

ABC A₃B₃C₃ ABC