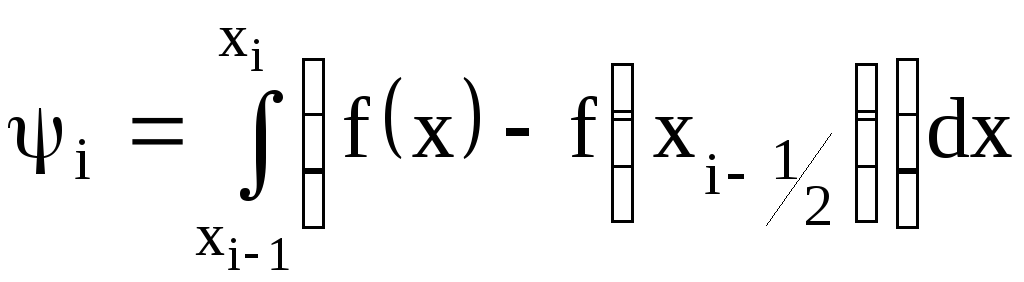1 Численное интегрирование

1.1 Основные методы численного интегрирования

В настоящем параграфе рассматриваются способы приближенного вычисления определенных интегралов

(1.1)

основанные на замене интеграла конечной суммой

(1.2)

где c_k – числовые коэффициенты и x_k – точки отрезка [a, b], k = 0, 1, …, n. Приближенное равенство

называется квадратурной формулой, а сумма вида (1.2) – квадратурной суммой. Точки x_k называются узлами квадратурной формулы, а числа c_k – коэффициентами квадратурной формулы. Разность

называется погрешностью квадратурной формулы. Погрешность зависит как от расположения узлов, так и от выбора коэффициентов. При оценке погрешности в приводимых ниже примерах функция f(x) предполагается достаточно гладкой.

Введем на [a,b] равномерную сетку с шагом h, т.е. множество точек

_h = {x_i = a + ih, i = 0,1,…,N, hN = b – a},

и представим интеграл (1.1) в виде суммы интегралов по частичным отрезкам:

Для построения формулы численного интегрирования на всем отрезке [a,b] достаточно построить квадратурную формулу для интеграла

(1.3)

на частичном отрезке [x_i-1,x_i] и воспользоваться свойством аддитивности определенного интеграла.

Формула прямоугольников.

Пользуясь малостью h, заменим интеграл (1.3) выражением , где . = x_i – 0,5h.

Тогда получим формулу

(1.4)

которая называется формулой прямоугольников на частичном отрезке [x_i-1,x_i].

Погрешность формулы (1.4) определяется величиной

которую легко оценить с помощью формулы Тейлора. Действительно, запишем _i в виде

(1.5)

и воспользуемся разложением

где _i = _i(x)  [x_i-1,x_i]. Тогда из (1.5) получим

Обозначая , оценим _i следующим образом:

Таким образом, для погрешности формулы прямоугольников на частичном отрезке справедлива оценка

(1.6)

т.е. формула имеет погрешность О(h³) при h  0.

Заметим, что оценка (1.6) является неулучшаемой, т.е. существует функция f(x), для которой (1.6) выполняется со знаком равенства. Действительно, для f(x) = (x – x_i-1/2)² имеем М_2,i = 2,

f(x_i-1/2) = 0 и

Суммируя равенства (1.4) по i от 1 до N, получим составную формулу прямоугольников (центральных прямоугольников)

(1.7)

Погрешность этой формулы

равна сумме погрешностей по всем частичным отрезкам,

Отсюда, обозначая , получим

(1.8)

т.е. погрешность формулы прямоугольников на всем отрезке есть величина О(h²).

В этом случае говорят, что квадратурная формула имеет второй порядок точности.

Замечание. Можно также использовать формулы прямоугольников при ином расположении узлов, например, такие формулы (формулы левых и правых прямоугольников соответственно):

Однако, из-за нарушения симметрии погрешность таких формул является величиной О(h).

Формула трапеций.

На частичном отрезке эта формула имеет вид

(1.9)

и получается путем замены подынтегральной функции f(x) интерполяционным многочленом первой степени, построенным по узлам x_i-1, x_i, т.е. функцией

Для оценки погрешности достаточно вспомнить, что

Отсюда получим

и, следовательно,

(1.10)

Оценка (1.10) неулучшаема, так как в ней достигается равенство, например, для f(x) = (x – x_i)².

Составная формула трапеций имеет вид

(1.11)

где f_i = f(x_i), i = 0, 1, …, N, x_i = a + ih, hN = b – a.

Погрешность этой формулы оценивается следующим образом:

Таким образом, формула трапеций имеет, так же как и формула прямоугольников, второй порядок точности,  = О(h²), но ее погрешность оценивается величиной в два раза большей (см. (1.8)).

Формула Симпсона.

При аппроксимации интеграла (1.3) заменим функцию f(x) параболой, проходящей через точки (x_j, f(x_j)), j = i – 1, i – 0,5, i, т.е. представим приближенно f(x) в виде

f(x)  L_2,i(x), x  [x_i-1, x_i],

где L_2,i(x) – интерполяционный многочлен Лагранжа второй степени,

(1.12)

Проводя интегрирование, получим

Таким образом, приходим к приближенному равенству

(1.13)

которое называется формулой Симпсона или формулой парабол.

На всем отрезке [a, b] формула Симпсона имеет вид

Чтобы не использовать дробных индексов, можно обозначить

x_i = a + 0,5hi, f_i = f(x_i), i = 0, 1, …, 2N, hN = b - a

и записать формулу Симпсона в виде

(1.14)

Прежде чем переходить к оценке погрешности формулы (1.13), заметим, что она является точной для любого многочлена третьей степени, т.е. имеет место точное равенство

если, f(x) = a₀ + a₁x + a₂x² + a₃x³. Это утверждение нетрудно проверить непосредственно, что и предоставляется сделать читателю.

Для оценки погрешности формулы Симпсона построим многочлен третьей степени Н₃(х) такой, что

H₃(x_i-1) = f(x_i-1), H₃(x_i-1/2) = f(x_i-1/2),

Известно, что такой многочлен существует и единственен. Он построен в явном виде. Однако нам даже не потребуется явный вид многочлена Н₃(х). Вспоминая, что формула Симпсона точна для любого многочлена третьей степени, получим

(1.15)

Представим теперь f(x) в виде

f(x) = H3(x) + ri(x), x  [xi-1, xi],

(1.16)

где r_i(x) – погрешность интерполирования многочленом Н₃(х). Интегрируя (1.16) и учитывая (1.15) получим

(1.17)

Имеем

поэтому для погрешности _i получаем оценку

где .

Вычисляя интеграл, приходим окончательно к оценке

(1.18)

Погрешность составной формулы Симпсона (1.14) оценивается так:

Отсюда видно, что формула Симпсона существенно точнее, чем формулы прямоугольников и трапеций. На частичном отрезке она имеет точность О(h⁵), а на всем отрезке – О(h⁴).