5.3 Означення I властивостi простих та складених чисел. Решето Ератосфена. Канонiчна форма натурального числа. Розподiл простих чисел серед чисел натурального ряду.

Номери ваших індивідуальних завдань обчислюються за формулою (А + 25k)(mod74), k = 0  5, де A  порядковий № за журналом,  порядковий номер навчальної групи. Вибираються номери записані нежирним шрифтом.

Зміст задач та завдань.

3.5. Чи є числа

5.3.5. а) 127, 919;

5.3.2. б) 1033, 1643;

5.3.3. в) 1657, 2647;

5.3.3. г) 2773, 3163;

5.3.4. д) 3621, 3623;

5.3.5. е) 3631, 3767;

5.3.5. є) 3769, 7429 простими?

3.2. Знайти всi простi числа, якi мiстяться мiж числами:

5.3.6. а) 1 i 100; 5.3.10. д) 1250 i 1300;

5.3.7. б) 100 i 150; 5.3.15. е) 2300 i 2350;

5.3.8. в) 150 i 200; 5.3.12. є) 2550 i 2600;

5.3.9. г) 550 i 600; 5.3.13. ж) 4300 i 4350.

3.3. Знайти канонiчний розклад числа n, якщо:

5.3.14. а) n = 160; 5.3.19. е) n = 1800;

5.3.15. б) n = 494; 5.3.20. є) n = 3551;

5.3.16. в) n = 1001; 5.3.25. ж) n = 82798848;

5.3.17. г) n = 1009; 5.3.22. з) n = 81057226635000.

5.3.18. д) n = 1769.

3.4. Довести, що дане число a є складеним, якщо:

5.3.23. а) ;

5.3.24. б) (теорема Софii Жермен);

5.3.25. в) , n > 1;

5.3.26. г) ;

5.3.27. д) , n > 5.

3.5. Знайти канонiчний розклад числа а, якщо:

5.3.28. а) a = ; 5.3.32. д) a = ;

5.3.29. б) a = ; 5.3.33. е) a = ;

5.3.30. в) a = ; 5.3.34. є) a = ;

5.3.35. г) a = ;

3.6. Знайти таке просте число n, щоб простими були також числа:

5.3.35. а) n + 5; 5.3.39. д) n + 4 i n + 14;

5.3.36. б) ; 5.3.40. е) n + 2 i n + 4;

5.3.37. в) ; 5.3.45. є) i ;

5.3.38. г) n + 10; 5.3.42. ж) 2n + 1 i 4n +5.

5.3.44. 3.7. Довести, що три числа n, n + m, n + n не можуть бути одночасно прос-тими, якщо n > 3 i натуральнi числа m i n дають при дiленнi на 3 вiдповiдно остачi 1 i 2.

5.3.45. 3.8. Довести, що з усiх цiлих чисел виду 2n + 1, де n – просте число, тiльки одне є точним кубом.

3.9. Довести, що одночасно простими не можуть бути такi числа:

5.3.46. а) n + 5 i n + 10;

5.3.47. б) n, n + 2, n + 5;

5.3.48. в) i , де n > 2.

5.3.49. 3.10. Нехай n  просте число i n > 5. Довести, що n² при дiленнi на 30 дає остачу 1 або 19.

3.15. Нехай n_k є k-те просте число (, , , i т.д.). Довести, що:

5.3.50. а) , причому рiвнiсть виконується тiльки при k = 1;

5.3.55. б) , де k 5;

5.3.52. в) ,

5.3.53. г) де n i n > 2.

5.3.54. 3.12. Довести, що коли пронумерувати всi простi числа, починаючи з 5, тобто , , i т.д., то > 3n.

5.3.55. 3.13. Нехай , n є N. Показати, що коли є просте число, то простим є також число n.

Примiтка. Простi числа виду називаються числами Мерсенна². Нинi вiдомо 27 чисел Мерсенна, причому 27е число дiстали при n = = 44497. Скiнченною чи нескiнченною є множина чисел Мерсенна невiдомо.

5.3.56. 3.14. Нехай , n є N. Довести, що коли просте число, то , де k  деяке цiле невiд'ємне число.

Примiтка. Простi числа виду називаються числами Ферма³. Досi не знайдено жодного простого числа виду при k > 5 (при k = 0, 1, 2, 3, 4 числа є простими), а також невiдомо, скiнченною чи нескiнченною є множина чисел Ферма.

5.3.57. 3.15. Довести, що кратно 24, якщо n i q  простi числа, бiльшi вiд 3.

5.3.58. 3.16. 3найти всi простi числа, якi є одночасно сумами i рiзницями простих чисел.

5.3.59. 3.17. Нехай р  просте число i р 5. Довести, що 24.

5.3.60. 3.18. Довести, що для будь-якого n N знайдеться таке х N, що nx + 1 є складене.

3.19. Знайти натуральне число n, якщо:

5.3.65. а) де деякi натуральні числа;

5.3.62. б) , де деякi натуральні числа.

5.3.63. 3.20. Довести, що мiж натуральними числами n i n!, де n > 2, мiститься, принаймнi, одне просте число.

3.25. Знайти n послiдовних складених натуральних чисел, якщо:

5.3.64. а) n = 10;

5.3.65. б) n = 12;

5.3.66. в) n = 100;

5.3.67. г) n =1000;

5.3.68. д) n = k.

3.22. Довести нескiнченнiсть множини простих чисел виду:

5.3.69. а) р =3k + 2, k N;

5.3.70. б) р = 3k + 1, ;

5.3.75. в) р = 4k + 1, ;

5.3.72. г) р = 4k + 3, ;

5.3.73. д) р = 6k + 1, ;

5.3.74. е) р = 6k + 5, .

5.4 Ланцюговi дроби. Пiдхiднi дроби ланцюгового дробу. Практичне використання неперервних дробів. Розв'язання у цілих числах лінійного рівняння з двома невідомими. Застосування методу ланцюгових дробів для факторизації цілих чисел.

Номери ваших індивідуальних завдань обчислюються за формулою (А + 25k)(mod113), k = 0  5, де A  порядковий № за журналом,  порядковий номер навчальної групи. Вибираються номери записані нежирним шрифтом.

Зміст задач та завдань.

4.5. Розкласти в ланцюгові дроби і обчислити їхні підхідні дроби для раціональних чисел:

5.4.1. а) ; 5.4.7. є) ;

5.4.2. б) ; 5.4.8. ж) ;

5.4.3. в) 2,55; 5.4.9. з) ;

5.4.4. г) ; 5.4.10. к) ;

5.4.5. д) ; 5.4.11. л) .

5.4.6. е) ;

4.2. За допомогою розкладу в ланцюгові дроби скоротити дроби:

5.4.12. а) ; 5.4.16. д) ; 5.4.20. з) ;

5.4.13. б) ; 5.4.17. е) ; 5.4.21. к) ;

5.4.14. в) ; 5.4.18. є) ; 5.4.22. л) .

5.4.15. г) ; 5.4.19. ж) ;

4.3. Знайти звичайні нескоротні дроби, що відповідають ланцюговим дробам:

5.4.23. а) [2; 1, 3, 4, 2]; 5.4.29. є) [  3; 1, 2, 1, 1, 5];

5.4.24. б) [2; 1, 19, 1, 3]; 5.4.30. ж) [  5; 2, 1, 1, 3, 2];

5.4.25. в) [2; 1, 1, 3, 1, 2]; 5.4.31. з) [1; 3, 2, 4, 3, 1, 1, 1, 5];

5.4.26. г) [1; 1, 2, 3, 4]; 5.4.32. к) [a; a, a, a, a];

5.4.27. д) [0; 4, 1, 2, 5, 6]; 5.4.33. л) [a; b, a, b, a].

5.4.28. е) [  2; 1, 3, 1, 1, 5];

5.4.34. 4.4. Нехай передостанній підхідний дріб у розкладі раціонального числа в ланцюговий дріб. Довести, що (a, b) = (1)^n1B_n1 a + (1)ⁿA_{n 1}b.

35. 4.5. Користуючись результатом задачі 4.4., розв'язати задачу 4.3.

6. Розв’язати рівняння:

5.4.36. а) ; 5.4.37. б) .

5.4.38. 4.7. Знайти ланцюговий дріб якщо , .

5.4.39. 4.8. Нехай для деякого скінченного ланцюгового дробу маємо , , . Знайти .

5.4.40. 4.9. Треба побудувати зубчасту передачу за допомогою двох валів з кількістю зубців, що дорівнює відношенню 587:113. Чи можна замінити це відношення чисельниками і знаменниками, але похибкою, яка не перевищує 0,001? Як зміниться відповідь, коли: а) початкове відношення 355:113, а похибка 0,002; б) початкове відношення 12532:3921, а похибка 0,00005?

4.10. Розв'язати в цілих числах рівняння:

5.4.41. а) 38х + 117у = 209; 5.4.46. е) 37х + 23у = 15;

5.4.42. б) 119х  68у = 34; 5.4.47. є) 53х + 17у = 25;

5.4.43. в) 41х + 114у = 5; 5.4.48. ж) 64х  39у = 15;

5.4.44. г) 49х + 9у = 400; 5.4.49. з) 3827х + 3293у = 189;

5.4.45. д) 12х + 31у = 170; 5.4.50. к) 571х + 359у =  10.

4.15. Розв’язати в натуральних числах рiвняння:

5.4.51. а)

5.4.52. б)

5.4.53. в) .

5.4.54. 4.12. Розкласти число 100 на суму таких двох натуральних чисел, щоб одне з них ділилось на 7, а друге  на 15.

5.4.55. 4.13. Для настилання пiдлоги завширшки 3 м є дошки завширшки 11 i 13 см. Скiльки треба дощок рiзної ширини, якщо довжина кiмнати i довжина дощок однаковi, а дошки кладуть вздовж кiмнати?

5.4.56. 4.14. Для перевезення зерна є мiшки по 60 i 80 кг. Скiльки треба таких мiшкiв для перевезення 440 кг зерна?

5.4.57. 4.15. Скiльки бiлетiв 30 i 50 коп. можна купити на 14 крб. 90 коп.?

5.4.58. 4.16. Купили 30 птахiв за 30 монет однiєї вартостi; причому за кожних трьох горобцiв заплатили 1 монету, за кожнi двi горлиці також одну монету і за кожного голуба  по дві монети. Скільки купили птахів кожного виду?

5.4.59. 4.17. 26 студентів посадили разом 88 дерев, причому кожен студент І, ІІ і ІІІ курсу повинен був посадити відповідно 6, 4 і 2 дерева. Скільки було студентів І, ІІ і ІІІ курсу?

4.18. Розкласти в ланцюгові дроби такі квадратичні ірраціональності:

5.4.60. а) ; 5.4.61. б) ; 5.4.62. в) ; 5.4.63. г) ; 5.4.64. д) ; 5.4.65. е) ; 5.4.66. є) ; 5.4.67. ж) ; 5.4.68. з) ; 5.4.69. к) ; 5.4.70. л) ; 5.4.71. м) ; 5.4.72. н) .

4.19. Шляхом розкладення в ланцюговий дріб факторизувати числа: 5.4.73. а) 3337; 5.4.74. б) 2813; 5.4.75. в) 1177; 5.4.76. г) 1537; 5.4.77. д) 2147; 5.4.78. е) 2627; 5.4.79. є) 7361; 5.4.80. ж) 6169; 5.4.81. з) 4199; 5.4.82. к) 1577; 5.4.83. л) 12095.

4.20. Знайти квадратні рівняння з цілими коефіцієнтами, корені яких розкладаються в такі нескінченні періодичні ланцюгові дроби:

5.4.84. а) [10; (10, 20)]; 5.4.88. д) [(2, 4, 1, 3)];

5.4.85. б) [9; (1, 1, 2, 4, 2, 1, 1, 18)]; 5.4.89. е) [2; 1, 2, (1, 1, 3)];

5.4.86. в) [2; (1, 1, 3)]; 5.4.90. є) [1; 2, (3, 4)].

5.4.87. г) [1; (1, 2, 2, 1)];

4.21. Знайти квадратичну ірраціональність , якщо:

5.4.91. а) ; 5.4.92. б) .

4.22. Розкласти в ланцюговий дріб:

5.4.93. а) ; 5.4.95. в) ;

5.4.94. б) ; 5.4.96. г) .

5.4.97. 4.23. Знайти підхідні дроби у розкладі , якщо .

5.4.98. 4.24. Знайти другий підхідний дріб у розкладі кореня рівняння .

4.24. Довести, що:

5.4.99. а) ;

5.4.100. б) при розкладі ірраціональності в ланцюговий дріб;

5.4.101. в) дріб , є нескоротним;

5.4.102. г) ;

5.4.103. д) для дробу , в якому , ;

5.4.104. е) ;

5.4.105. є) ;

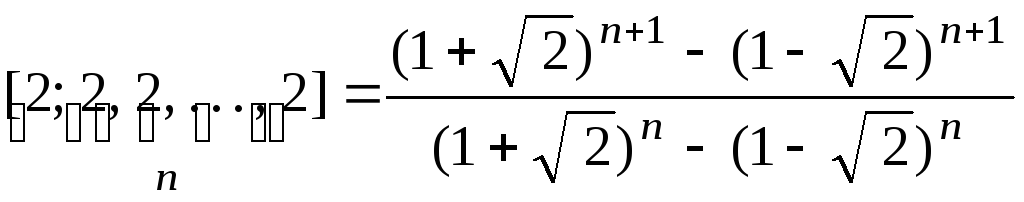5.4.106. ж) , якщо ;

5.4.107. з) або для заданого дійсного додатного числа і натурального числа ;

5.4.108. к) є підхідним дробом розкладу дійсного додатного числа у ланцюговий дріб, якщо і ;

26. Довести, що:

5.4.109. а) додатний корінь тричлена , де натуральні числа, розкладається в нескінченний чистий періодичний ланцюговий дріб, довжина періоду якого дорівнює 2;

5.4.109. б) квадратне рівняння з цілими коефіцієнтами має другий корінь , якщо перший його корінь є число ;

5.4.110. в) квадратне рівняння з цілими коефіцієнтами має корінь , якщо перший його корінь є число ;

5.4.111. г) числа і пропорційні числам і ;

5.4.112. д) ірраціональність виду розкладається в ланцюговий дріб, період якого починається з другої неповної частки.

5.4.113. 4.27. Знайти загальний вигляд квадратичних ірраціональностей, які розкладаються в ланцюговий дріб з однаковими неповними частками.