5.2. Найбiльший спiльний дiльник I найменше спiльне кратне та способи знаходження їх. Взаємно простi числа

Номери ваших індивідуальних завдань обчислюються за формулою (А + 25k)(mod100), k = 0  5, де A  порядковий № за журналом,  порядковий номер навчальної групи. Вибираються номери записані нежирним шрифтом.

Зміст задач та завдань.

2.1. Знайти найбiльший дiльник чисел:

5.2.1. а) 0 i 0; 5.2.7. є) 2585 i 7975;

5.2.2. б) 0 i 7; 5.2.8. ж) 2091 i 1681;

5.2.3. в)  231 i 546; 5.2.9. з) 3763 i 3337;

5.2.4. г) 1001 i 6253; 5.2.10. к) 6791400 i 178500;

5.2.5. д) 1066 i 1970; 5.2.11. л) 6791400 i 178500;

5.2.6. е) 1173 i 323; 5.2.12. м) чисел n та n +5.

2.2. Знайти найбiльший дiльник таких чисел:

5.2.7. а) 819, 702 i 689; 5.2.19. є) 42598, 2324 i 498;

5.2.8. б) 3059, 2737 i 943; 5.2.20. ж) 1023, 1518 i 14883;

5.2.9. в) 2737, 9163 i 9639; 5.2.21. з) 3655, 2516, 731 i 663;

5.2.10. г) 299, 391 i 667; 5.2.22. к) 91467, 3660 i 3360;

5.2.11. д) 588, 2058 i 2849; 5.2.23. л) Трьох послiдовних чи5.2.12. е) 31605, 13524, 12915 i 11067; сел n, n +1, n +2;

2.3. Знайти найменше спiльне кратне чисел:

5.2.13. а) 0 i 0; 5.2.29. е) 252 i 468;

5.2.14. б) 0 i 1; 5.2.30. є) 279 i 372;

5.2.15. в) 360 i 504; 5.2.31. ж) 178 i 387;

5.2.16. г) 187 i 533; 5.2.32. з) чисел n i n + 5.

5.2.17. д)  2520 i 6600;

2.4. Знайти найменше спiльне кратне чисел:

5.2.18. а) 126, 420 i 525; 5.2.36. г) n, n + 1 i n + 2;

5.2.19. б) 91, 252 i 462; 5.2.37. д) 1058, 1403 i 3266;

5.2.20. в) 84, 147 i 245; 5.2.38. е) 356, 1068 i 1424.

2.5. Знайти лiнiйне зображення найбільшего спільного дільника чисел:

5.2.21. а) 21 i 51; 5.2.44. е) 1786 i 705;

5.2.22. б)  26 i 174; 5.2.45. є) 822 i 173;

5.2.23. в) 899 i 493; 5.2.46. ж) 4373 i -826;

5.2.24. г) 1445 i 629; 5.2.47. з)  3791 i 3285.

5.2.25. д) 903 i 731;

2.6. Довести, що для довiльних натуральних a i b:

5.2.26. а) (a, b) = (a + b, a + 2b);

5.2.27. б) (a, b) = (2a + 2b, 3a + 4b);

5.2.28. в) (a, b) = (7a + 5b, 4a + 3b);

5.2.29. г) (a, b) = (3a + 5b, 8a + 13b);

5.2.30. д) (a, b) = (4a + 3b, 5a + 4b);

5.2.31. е) (a, b) = (ma + nb, ka + lb), де m, n, k, l  натуральнi числа, причому .

2.7. Знайти натуральнi числа a i b, якщо:

5.2.32. а) 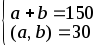; 5.2.61. ж) ;

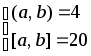5.2.33. б) ; 5.2.62. з) ;

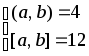5.2.34. в) 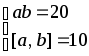; 5.2.63. к) ;

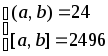5.2.35. г) 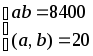; 5.2.64. л) ;

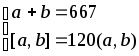5.2.36. д) 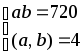; 5.2.65. м) ;

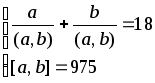5.2.37. е) 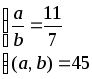; 5.2.66. н)

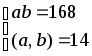
5.2.38. є) ;

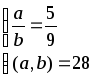2.8. Довести, що для довiльних натуральних a, b, c:

5.2.39. а) (a, b) = ( a, b) = (a, a ± b) = (a ± b, b);

5.2.40. б) (ab, bc, ca) кратно (a, b, c)²;

5.2.41. г) (a, b, c) = , якщо a, b, c  непарні числа;

5.2.42. д) [a, b, c] = ;

5.2.43. е) (a, b)(a, c)(b, c)[a, b][a, c][b, c] = a²b²c²;

5.2.44. є) abc = [a, b, c](ab, ac, bc);

5.2.45. ж) (a, [b, c]) = [(a, b), (a, c)];

5.2.46. з) [a, (b, c)] = ([a, b], [a, c]);

5.2.47. к) (aa₁, bb₁, ab₁, a₁b) = dd₁, якщо d = (a, b) i d₁ = (a₁, b₁);

5.2.48. л) ([a, b], (a, b)) = (a, b);

5.2.49. м) ([a, b], ab) = [a, b];

2.9. Довести, що для довiльних натуральних a, b, c:

5.2.50. а) (a, a +1) = (a +1, 2a + 1) = (a, 2a +1) = 1;

5.2.51. б) (a, 2a + 1) = (a, 2a  1) = 1;

5.2.52. в) ;

5.2.53. г) (14a + 3, 21a + 4) = 1;

5.2.54. д) (b  a, b) = 1, якщо (a, b) = 1;

5.2.55. е) (a + b, ab) = 1, якщо (a, b) = 1;

5.2.56. є) (a, a + b) = (a + b, 2a + b) = (a, 2a + b) = 1, якщо (a, b) = 1;

5.2.57. ж) (ac, b) = (c, b), зокрема с кратно (ac, b), якщо (a, b) = 1;

5.2.58. з) (a + b, a  b) = 1, або 2, якщо (a, b) = 1;

5.2.59. к) , якщо (a, b) = 1;

5.2.60. л) (11a + 2b, 18a + 5b) = 1, або 19, якщо (a, b) = 1;

5.2.61. м) ;

5.2.62. н) .

2.10. Знайти найбiльший дiльник чисел:

5.2.63. a) i , якщо а  цiле, а m i n  натуральнi;

5.2.64. б) i 2a + 3, якщо а  цiле;

5.2.65. в) i .

5.2.66. 2.11. Довести, що з п'яти послiдовних чисел завжди можна вибрати одне, взаємопросте з усiма iншими.

2.12. Довести, що

5.2.67. а) кратне 1897, де n  натуральне число;

5.2.68. б) n(n + 1)(n + 2) кратне 504, якщо n + 1 є кубом натурального числа;

5.2.69. в) кратне 30, якщо a  цiле, n  невiд'ємне число;

5.2.70. г) a³ b³ кратне тодi i тiльки тодi, коли a  b кратно , де a, b  цiлi непарнi числа, а n  натуральне число;

5.2.71. д) (a + 1, a^2k + 1) = 1, якщо a  парне натуральне число, k  натуральне число.