Тема 2. Числовi функцiї.

2.5. Число I сума натуральних дiльникiв. Цiла I дробова частини дiйсного числа. Функцiя Ейлера. Узагальнена функцiя Ейлера.

1. Знайти суму і число дiльникiв числа 680.

Р о з в ' я з а н н я: знаходимо канонічний розклад числа 680:

680 = 2^35^117^5.

Тодi

t(680) = (3 +1)(1 +1)(1 +1) = 16,

.

Дiльники числа 680 дiстанемо, коли розкриємо дужки у виразi

(1 + 2 + 4 + 8)(1 + 5)(1 + 17).

Матимемо:

1, 2, 4, 8, 5, 10, 20, 40, 17, 34, 68, 136, 85, 170, 340, 680.

2. Знайти натуральне х, якщо воно має тiльки 2 рiзних простих дiльники i , .

Р о з в'я з а н н я. Оскiльки число х має тiльки два рiзних простих дiльники (нехай це будуть числа p i q), то канонiчний розклад х має вигляд: , де y i z  натуральнi числа. Тодi

t(x) = (y +1)(z +1), .

Оскiльки 6, то (y +1)(z +1) = 6. Внаслiдок того, що числа y i z натуральні, y = 1, z = 2 або навпаки. Тодi x = pq² i, то (p + 1)(q² + q + 1). Оскільки , то (p + 1)(q² + q + 1) = 28.

Через те що p i q  рiзнi простi числа, слiд розглянути такі можливі випадки: p +1 = 4, q² + q + 1 = 7 або навпаки. Якщо p +1 = 4, q² + q + 1 = 7, то p = 3, , тодi x = 3^12² = 12. Якщо p + 1 = 7, q² + q + 1 = 4, то p = 6, що супере-чить вибору числа р. Отже, єдиним числом, яке задовольняє умову задачi, є число х = 12.

3. Знайти натуральне число n, якщо i , де натуральні числа.

Р о з в'я з а н н я. Оскiльки

,

то

600 =.

Звiдси

3²5³ = .

Ця рiвнiсть можлива тiльки при .Тодi n = 3^25³ = 1125.

4. Знайти кiлькiсть нулiв, якими закiнчується число 295!.

Р о з в'я з а н н я. Щоб розв'язати задачу, треба знайти канонiчний розклад заданого числа. Справдi, якщо , то кiлькiсть нулiв, якими закiнчується число, равно m, де m  меньше з чисел k i s, a k i s  показники чисел 2 i 5 вiдповiдно в канонiчному розкладi числа n!. Оскiльки до канонiчного розкладу n! просте 5 входить з меньшим показником, нiж просте 2, то для розв'язання задачi досить знайти s, з яким просте число 5 входить до добутку n!. Як вiдомо, s знаходять за формулою

.

Оскiльки 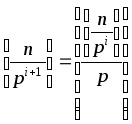, то для нашого прикладу маємо

.

Отже, число 295! закiнчується 72 нулями.

5. Довести, що, добуток усiх дiльників числа n дорівнює .

Д о в е д е н н я. Дільникі d числа у загальному випадку мають вигляд , де , . Добуток всіх дільників тоді можна подати так . Кожний з дільників включатиме по одному з співмножників кожного з m наборів: , , . . . , . Отже, з цих дільників можна побудувати усі дільники числа n. Кожне з чисел може увійти у дільники побудовані іншими числами (що входять у число )) способами. Тому число увійде в добуток D всіх дільників числа n рівно разів. В результаті приходимо до висновку, що свавільне просте число буде подано у добутку всіх дільників числа n у вигляді , а для добутку всіх дільників числа n можна записати подання

.

Тема 3. Теорія порівнянь з арифметичними застосуваннями

3.6 Порівняння в кільці цілих чисел та їхні найпростіші властивості

1. Чи порівняні числа 78, 210 і 346 з числом 27 за модулем 11?

Р о з в’я з а н н я. Віднімемо від даних чисел число 27. Дістанемо 51, 173 і 319. З них тільки 319 ділиться на 11, а тому тільки 346 порівняно з 27 за модулем 11, тобто 346  27(mod 11).

2. Довести, що коли 100a + 10b + c  0(mod 21), то a  2b + 4c  0(mod 21), a, b, c  Z.

Д о в е д е н н я. Нехай 100a + 10b + c  0(mod 21). Помноживши обидві частини цього порівняння на 4, матимемо

400a + 40b + 4c  0(mod 21). (1)

При цьому мають місце порівняння:

400a  a(mod 21), бо 400a – a = 399a 21, (2)

40b  – 2b (mod 21), бо 40b – (–2b) = 42b 21, (3)

4c  4c (mod 21), бо 4c – 4c = 0 25. (4)

Додавши почленно ці порівняння, дістанемо

400a + 40b + 4c  a  2b + 4c (mod 21). (5)

Беручи до уваги конгруенцію (1), матимемо

a  2b + 4c  0 (mod 21).

3. Знайти остачу иід ділення 1532⁵  1 на 9.

Р о з в ’ я з а н н я . Зрозуміло, що нераціонально знаходити число 1532⁵  1, а потім остачу від ділення цього числа на 9. Слід скористатися властивостями порівнянь за модулем 9. Нам треба знайти таке ціле невід’ємне число x, що (mod 9) і x < 9. Оскільки 1530 9, то 1532⁵  (1532  1530)⁵(mod 9), тобто 1532⁵  2⁵ (mod 9). Проте 2⁵ = 32  5 (mod 9). Отже, 1532⁵  5 (mod 9). Віднімемо почленно від цього порівняння порівняння 1  1(mod 9). Матимемо 1532⁵  1. Оскільки 0 < 4 < 9, то x = 4. Отже, число 1532⁵  1 при діленні на 9 дає остачу 4.

4. Довести, що числа виду 3+ 2, n  N є складеними.

Р о з в’я з а н н я. Оскільки 4   1 (mod 5), то 2^{4n + 1} = 24²ⁿ  2 (mod 5). Тоді число 2^{4n + 1} має вид 5k + 2, де k  N, а тому 3+ 2 = 3^{5k + 2} + 2 при деякому k. Оскільки , a , то 3^{5k + 2} + 2 = 9 243^k + 2  0 (mod 11). Отже, 3+ 2 ділиться на 15. Беручи до уваги нерівність 3+ 2 > 11, приходимо висновку, що 3+ 2 є складене число.