Тема 5. Теорія подільності в кільці цілих чисел
5.4 Ланцюговi дроби. Пiдхiднi дроби ланцюгового дробу
-
Розкласти в ланцюговий дріб число
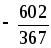і знайти всі підхідні дроби.
Р
о з в я
з а н н я. Якщо
додатний дріб, то застосовуємо алгоритм
Евкліда. Якщо
,
то спочатку подаємо його у вигляді
,
де
натуральне
число, а
правильний
дріб. Отже маємо
.
Далі, за алгоритмом Евкліда дістаємо
-
367
132
264
2
132
103
103
1
103
29
87
3
29
16
16
1
16
13
13
1
13
3
12
4
31
3
3
0
Отже,
,
зокрема,
,
.
Для обчислення підхідних дробів складаємо
таблицю 3.
Т а б л и ц я 3
-
k
1
0
1
2
3
4
5
6
7
qk
2
2
1
3
1
1
4
3
Ak
1
2
3
5
18
23
41
187
602
Bk
0
1
2
3
11
14
25
114
367
Звідси:
Зауваження
1.
Оскільки
то нижні дві клітинки останнього
стовпчика в таблиці для обчислювання
підхідних дробів є своєрідною перевіркою
правильності виконання всіх обчислень.
2.
Якщо звичайний дріб
розкласти в ланцюговий, то останній
підхідний дріб
буде нескоротний, ланцюговий дріб дає
змогу водночас скорочувати дріб
.
3.
Обчисливши всі підхідні дроби за даним
ланцюговим дробом
[q0;
q1,
q2,
..., qn]
можна дістати нескоротний дріб
,
що відповідає йому.
-
Ірраціональне число
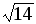розкласти в ланцюговий дріб і обчислити
з точністю до 0,0001 значення .
Р
о з в' я з а н н я. Щоб розкласти дійсне
число
в ланцюговий дріб, використовують
алгоритм Ейлера
алгоритм виділення цілої частини. У
згоді з приведеним раніше алгоритм
Ейлера записується таким чином
=
q0
+
,
де q0
=
і
>1;
=
q1
+
,
де q1
=
і
>1;
=
q2
+
,
де q2
=
i
>1,
. . . . . . . . . . . . . . . . . . .
Про
послiдовнiсть q0;
q1,
q2,
... кажуть, що її побудовано з числа
за допомогою алгоритму видiлення цiлої
частини. Всi члени цiєї послiдовностi
цiлi числа, причому
для i
=
1, 2, ....
Процес
побудови цiєї послiдовностi закiнчується
тодi, коли деяке
n
буде
цiлим числом (тобто тодi, коли
n+1
=
1).
Якщо
рацiональне число, тобто
=
,
де a
Z,
b
N,
то застосовуючи алгоритм Евклiда до
i до чисел a
i
b,
дiстанемо ту саму послiдовнiсть. Тодi
матимемо скiнченну послiдовнiсть q0;
q1,
q2,
..., qn
i
розклад числа
=
в скiнченний ланцюговий дрiб:
Якщо
iррацiональне число, то, очевидно,
послiдовнiсть q0;
q1,
q2,
... нескiнченна (тодi всi
i
> 1, i
=
1, 2, ...).
Використовуючи
алгоритм видiлення цiлої частини для
числа
,
маємо:
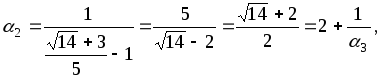
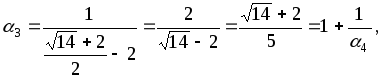
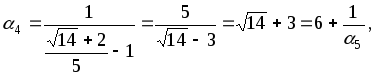
За
наближене значення
можна взяти один з пiдхiдних дробiв
побудованого ланцюгового дробу. Для
обчислення пiдхiдних дробiв складаємо
таблицю (табл. 4)
Таблиця 4
-
k
1
0
1
2
3
4
5
6
7
...
qk
3
1
2
1
6
1
2
1
...
Ak
1
3
4
11
15
101
116
333
449
...
Bk
0
1
1
3
4
27
31
89
120
...
Отже,
=
.
Для обчислень можна скористатися і схемою за таблицею2 (табл.5).
Таблиця 5
-
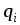
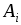
1
1
0
0
1
3
3
1
3
5
1
4
2
2
2
2
153
3
2
5
1
230
4
3
1
6
383
5
3
5
1
613
6
2
2
2
3448
7
2
5
1
4061
8
3
1
6
1638
...
...
...
...
...
Як
вiдомо, похибка наближення числа
пiдхiднiм дробом
не перевищує
або
.
Оскiльки
в даному разi
< 0,0001, то за наближення
з точнiстю до 0,0001 можна взяти пiдхiдний
дрiб
,
тобто
3,7416.
Зауваження.
Будь-який наступний за
пiдхiднiй дрiб буде точнiшим рацiональним
наближенням до
.
Проте краще вибирати за наближення той
з пiдхiдних дробiв, в якого знаменник
найменший.
3.
Знайти квадратичну iррацiональнiсть
,
якщо
= [4; 3, (2, 1)].
Розв’язання. Перетворимо спочатку нескiнченний чистий перiодичний ланцюговий дрiб, який дiстаємо iз заданого ланцюгового дробу пiсля того, як вiдкинемо цифри, що стоять до перiоду:
y
=
[(2, 1)] = 2
.
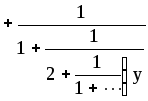Маємо
y
= 2
,
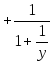Звідки
.
Оскiльки
y
додатна квадратична iррацiональнiсть,
то y
=
1 +
.
Тепер перетворимо в квадратичну
iррацiональнiсть заданий нескiнченний
мiшаний перiодичний ланцюговий дрiб:
[4;
3, (2, 1)] = [4; 3, y]
= 4 +
.
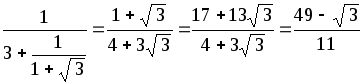Отже,
[4;
3, (2, 1)] =
.
4. Розв’язати в цiлих числах рiвняння: 117x + 343y = 119.
Р о з в’я з а н н я. Запишемо це рiвняння так:
117( x) + 343y = 119.
Визначимо невiдомi x та y. Загальний розв’язок у цiлих числах рiвняння ax + by = c, де a, b, c цiлi числа й (a, b) = 1, подамо у виглядi
x
=
(1)n-1c
+
bt
y
=
(1)nc
at,
де
t
довiльне цiле число, а An-1
i
Bn-1
чисельник i знаменник передостаннього
пiдхiдного дробу розкладу
у ланцюговий дрiб.
У цьому разi a = 117, b = 343, (117, 343) = 5.
Розкладемо
дрiб
в ланцюговий: a
=
[0; 2, 1, 13, 1, 1, 1, 2].
Отже,
n
=
7. Обчислимо
=
A6
i
=
B6.
Маємо A6
=
44, B6
=
129.
То одним з окремих розв’язкiв є
x0 = (1)6·119·129 = 15351, y0 = (1)7·119·44 = 5236.
Згiдно з формулами (2), загальний розв'язок рiвняння запишемо як
x = 15351 + 343t, y= 5236 117t,
або
x = 15351 343t, y = 5236 117t.
Маємо порiвняно великi за абсолютною величиною окремi значення для x0 i y0, проте iз загального розв'язку можна дiстати iншi окремi значення для x i y, якi будуть найменшi за абсолютною величиною. Нехай t = 44. Тодi
x = 84 + 343k, y = 29 + 117k (тут замiнено t на k).
Зауваження.
1. У розглянутому прикладі значення x i y можна було визначити відразу.
Справді,
розкладаючи
в ланцюговий дріб, дістаємо
.
Тоді
n
=
8, a
=
117, b
=
343, c
=
119,
=
A7
=
44,
=
B7
=
129. Згідно з формулами (2),
x0 = (1)7·119·129 = 15351, y0 = (1)8·119·( 44) = 5236.
Отже, x = 15351 343t, y = 5236 117t.
При t = 45 маємо той самий результат, що й раніше:
x = 84 + 343t, y = 29 + 117t.
-
Часто при розв'язуванні аналогічних задач треба обчислити тільки підхідний дріб
.
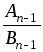Проте
доцільно заповнювати всю таблицю для
підхідніх дробів, оскільки, обчисливши
дріб
,
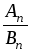можна перевірити розв'язання.
4.
Факторізувати число
шляхом розкладення кореня квадратного
з цього числа в ланцюговий дріб. У цій
задачі скористуємося результатами (5)
і (6): Обчислюємо
= 76,
.
Далі
для
розраховуємо
,
,
и
остача от ділення числа
на число
.
Результати розрахунків за навденими
формулам зведені у таблицю 4.
Таблиця 4
-
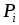
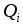
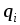
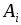
1
1
0
0
1
76
76
1
76
95 = 519
1
77
2
19
58 = 229
1
153
3
39
75 = 352
1
230
4
36
61
1
383
5
25
86 = 243
1
613
6
61
25 = 52
5
3448
7
64
71
1
4061
8
7
82 = 241
1
1638
9
75
3
50
З
таблиці дістаємо:
.
З цього рівняння маємо
103.
Отже, 5871 = 57103.
Другим
вариантом рішення буде 753
= 5232
= (1531638)2
= 40322 +
.
Отже, в данному випадку маємо (4032
15, 5871) = 103. В той же час (4032 + 15, 5871) = 57.