5.9. Порівняння першого степеня з одним невідомим та їх застосування.

Номери ваших індивідуальних завдань обчислюються за формулою (А + 25k)(mod 130), k = 0  5, де A  порядковий № за журналом,  порядковий номер навчальної групи. Вибираються номери записані нежирним шрифтом.

Зміст задач та завдань

9.5. За способом спроб розв’язати такі порівняння:

5.9.1. а) 2x  1(mod 3); 5.9.5. д) 4x  6(mod 10);

5.9.2. б) 8x  3(mod 4); 5.9.6. е) 12x  1(mod 7);

5.9.3. в) 6x  7(mod 5); 5.9.7. є) 5x  7(mod 11);

5.9.4. г) 3x  22(mod 7); 5.9.8. ж) 8x  16(mod 12).

9.2. За штучним способом розв’язати такі порівняння:

5.9.9. а) 7x  8(mod 13); д) 16x  50(mod 23);

5.9.10. б) 6x  11(mod 14); 5.9.13. е) 25x  1(mod 37);

5.9.11. в) 8x  10(mod 14); 5.9.14. є) 17x  23(mod 41);

5.9.12. г) 11x  -32(mod 27); 5.9.15. ж) 32x  43(mod 39).

9.3. За способом Ейлера розв’язати такі порівняння:

5.9.16. а) 5x  7(mod 13); 5.9.21. д) 27x  11(mod 34);

5.9.17. б) 29x  3(mod 12); 5.9.22. е) 24x  1(mod 15);

5.9.18. в) 5x  26(mod 12); 5.9.23. є) 15x  23(mod 22);

5.9.19. г) 8x  17(mod 19); 5.9.24. ж) 12x  51(mod 39).

9.4. Застосовуючи ланцюгові дроби, розв’язати такі порівняння:

5.9.25. а) 15x  37(mod 98); 5.9.31. є) 192x  9(mod 327);

5.9.26. б) 32x  182(mod 119); 5.9.32. ж) 365x  50(mod 395);

5.9.27. в) 105x  72(mod 147); 5.9.33. з) 639x  177(mod 924);

5.9.28. г) 97x  53(mod 169); 5.9.34. к) 1296x  1105(mod 2413);

5.9.29. д) 50x  67(mod 177); 5.9.35. л) 1215x  560(mod 2755);

5.9.30. е) 69x  393(mod 201); 5.9.36. м) 1919x  1717(mod 4009).

9.5. Застосовуючи класи лишків, розв’язати такі порівняння:

5.9.37. а) 21x  17(mod 23); 5.9.41. д) 28x  33(mod 35);

5.9.38. б) 5x  7(mod 24); 5.9.42. е) 12x  24(mod 30);

5.9.39. в) 17x  19(mod 24); 5.9.43. є) 9x  18(mod 41);

5.9.40. г) 13x  1(mod 30); 5.9.44. ж) 11x  31(mod 50);

9.6. Розв’язати штучним способом порівняння:

5.9.45. а) 5x  7(mod 13); 5.9.49. д) 27x  11(mod 34);

5.9.46. б) 29x  3(mod 12); 5.9.50. е) 24x  1(mod 15);

5.9.47. в) 5x  26(mod 12); 5.9.51. є) 15x  23(mod 22);

5.9.48. г) 8x  17(mod 19); 5.9.52. ж) 12x  51(mod 39).

5.9.52. з) 21x  17(mod 23); 5.9.56. м) 28x  33(mod 35);

5.9.53. и) 5 x  7(mod 24); 5.9.57. н) 12 x  24(mod 30);

5.9.54. к) 17 x  19(mod 24); 5.9.58. о) 9 x  18(mod 41);

5.9.55. л) 13x  1(mod 30); 5.9.59. п) 11x  31(mod 50).

9.7. Розв’язати такі порівняння:

5.9.60. а) (a + b)x  a² + b²(mod ab), (a, b) = 1;

5.9.61. б) (a² + b²)x  a - b(mod ab), (a, b) = 1;

5.9.62. в) (a + b)²x  a² - b²(mod ab), (a, b) = 1;

5.9.63. г) (a – b)x  a² + b²(mod ab), (a, b) = 1;

5.9.64. д) 2x  1+ p(mod p), де p  просте непарне число;

5.9.65. е) (m – 1)x  1(mod m);

5.9.66. є) (m + 1)²x  a(mod m);

5.9.67. ж) ax  1(mod p), де p  просте число і (a, p) = 1;

9.8. Скласти порівняння першого степеня з одним невідомим за модулем 15 так, щоб вона мала:

5.9.68. а) єдиний розв’язок;

5.9.69. б) 3 або 5 розв’язків;

5.9.70. в) 2, 4, 6, 14 розв’язків;

14.9. Розв’язати в цілих числах невизначені рівняння:

5.9.71. а) 2x + 3y = 4; 5.9.78. ж) 17x – 16y = 31;

5.9.72. б) 4x – 3y = 2; 5.9.79. з) 91x – 28y =35;

5.9.73. в) 3x + 4y = 13; 5.9.80. к) 17x – 39y = 26;

5.9.74. г) 5x + 4y = 3; 5.9.81. л) 50x – 42y =34;

5.9.75. д) 3x + 8y = 5; 5.9.82. м) 47x – 105y = 4;

5.9.76. е) 17x + 13y = 1; 5.9.83. н) 47x – 111y = 89;

5.9.77. є) 23x + 15y = 19;

9.10. Розв’язати системи порівнянь:

5.9.84. а) 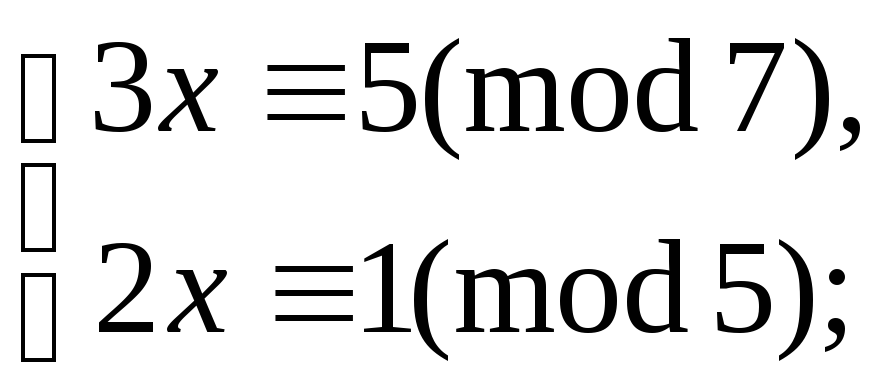5.9.88. д)

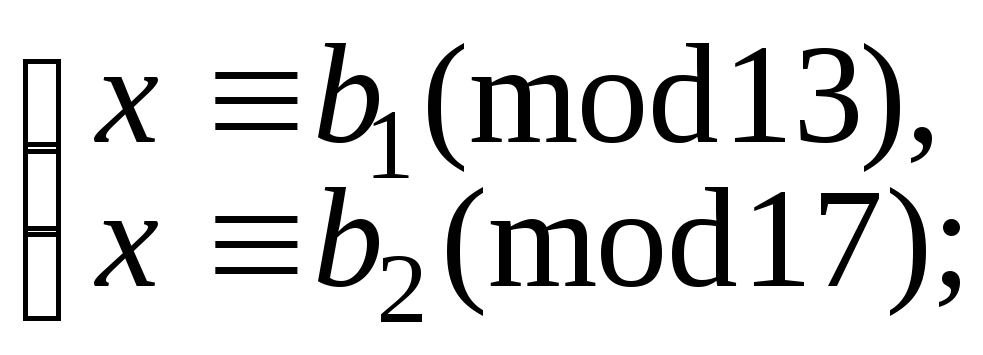
5.9.85. б) 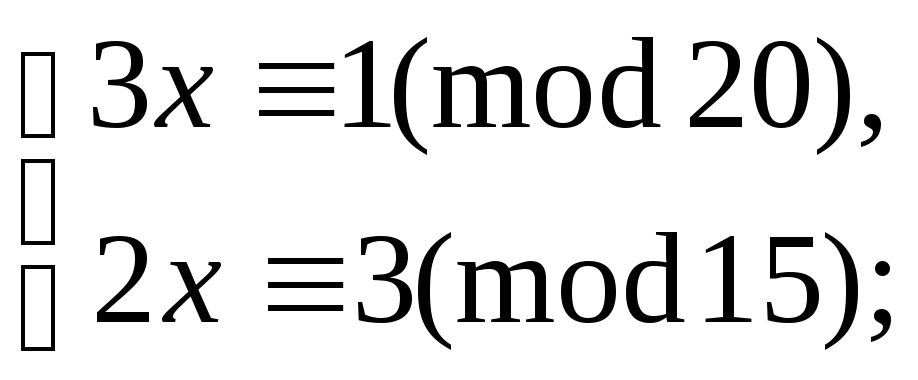5.9.89. е)

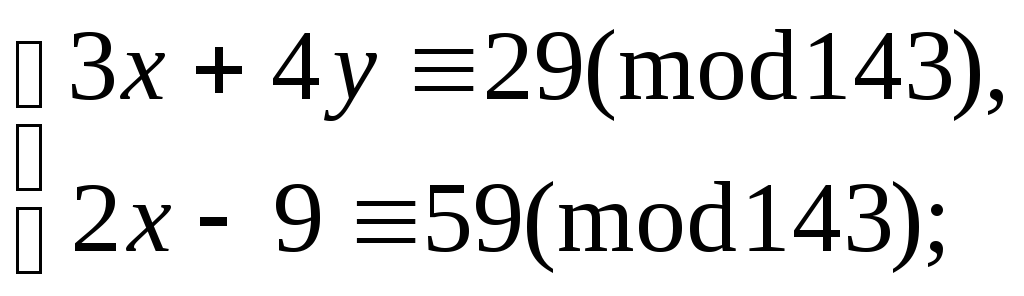
5.9.86. в) 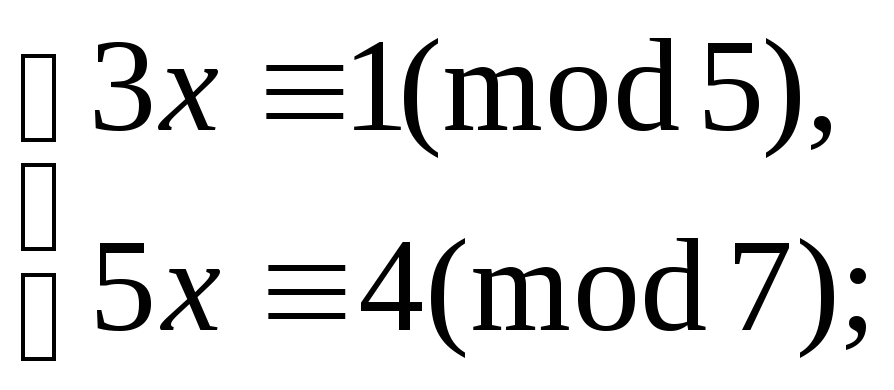5.9.90. є)

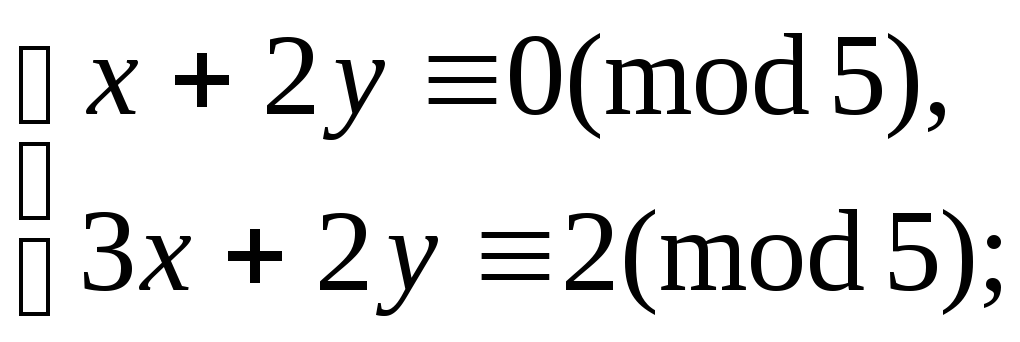
5.9.87. г) 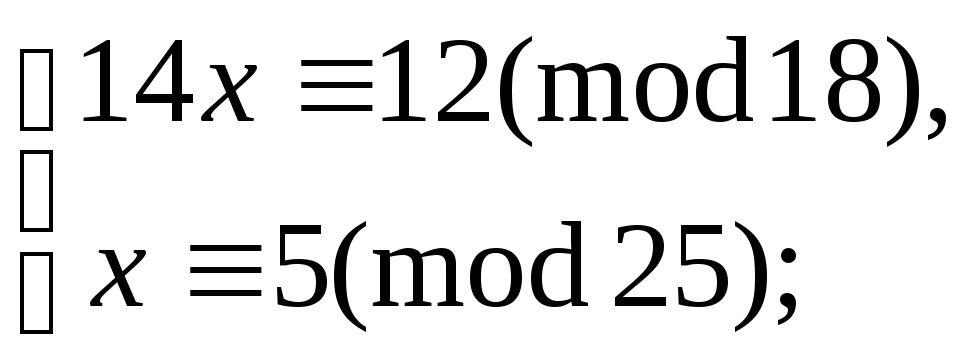5.9.91. ж)

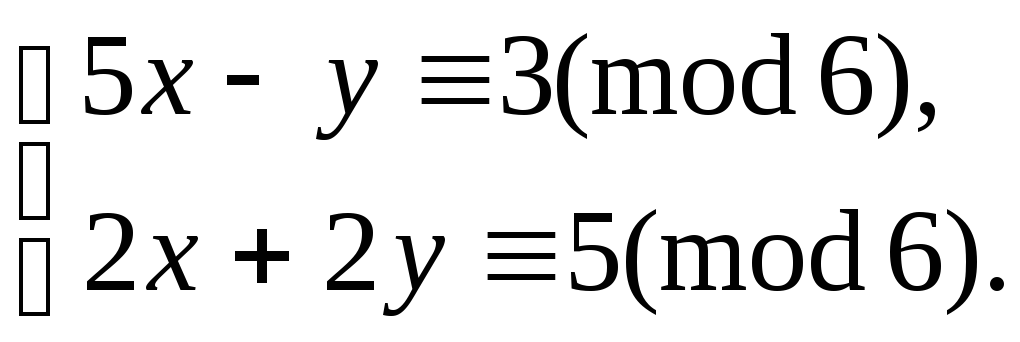
9.15. Розв’язати системи порівнянь:

5.9.92. а) 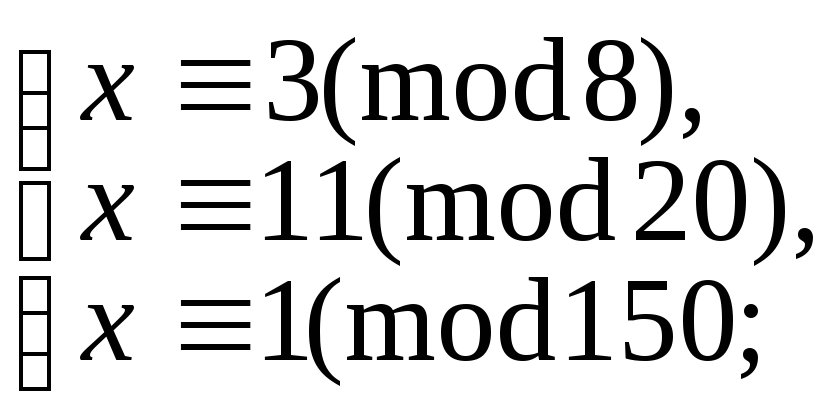5.9.98. е)

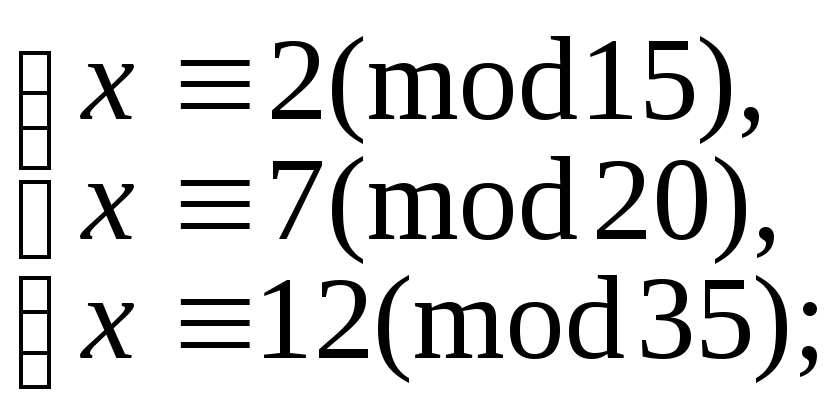
5.9.93. б) 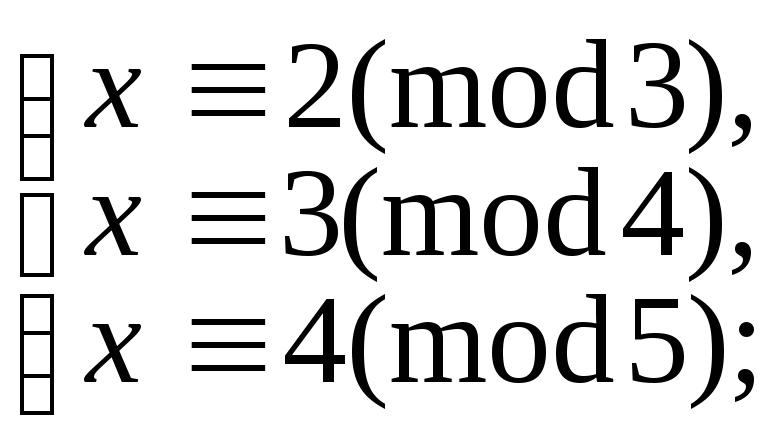5.9.99. є)

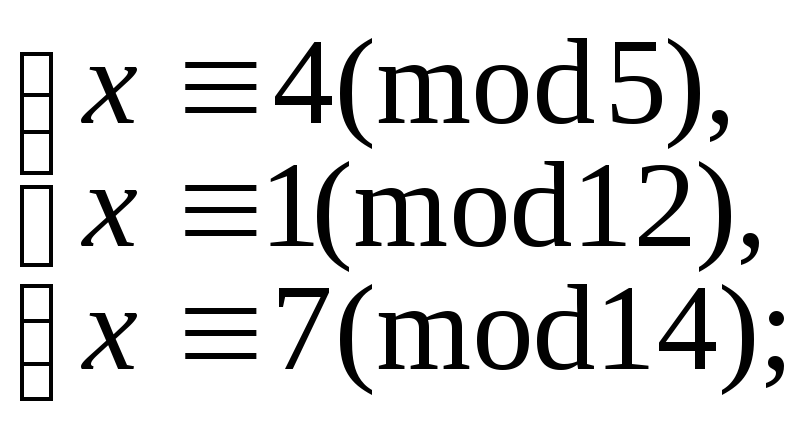
5.9.94. в) 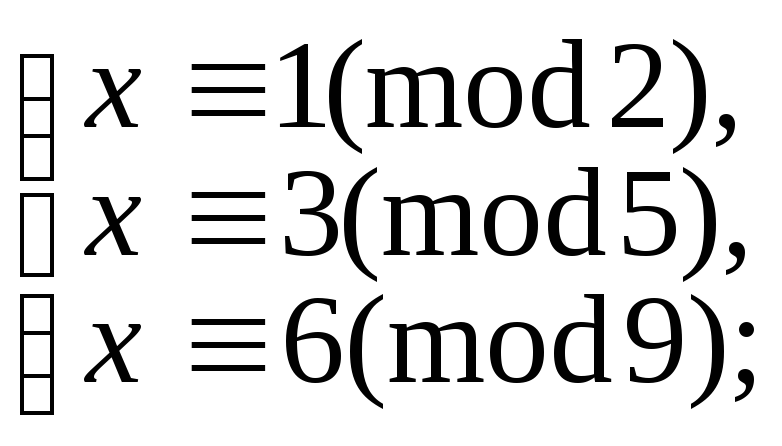5.9.100. з)

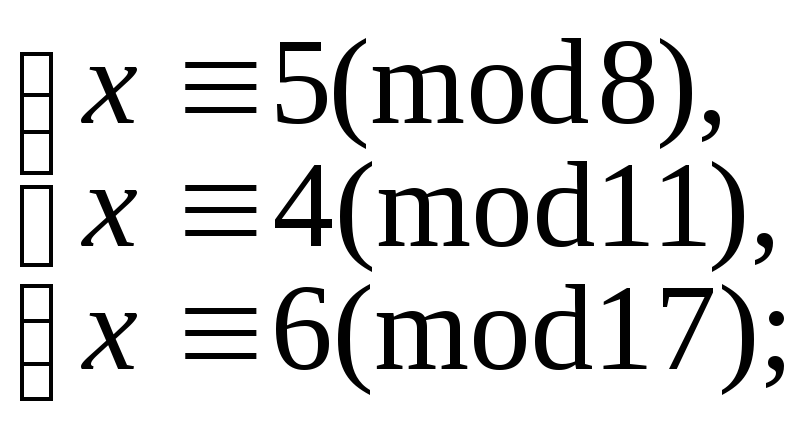
5.9.95. г) 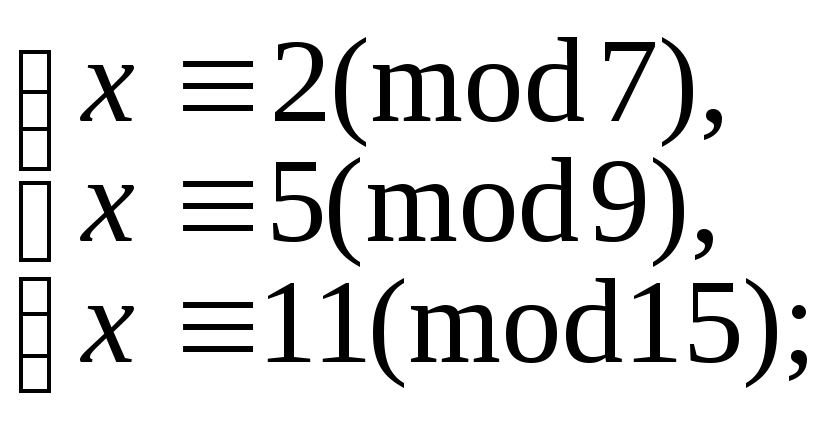5.9.101. к)

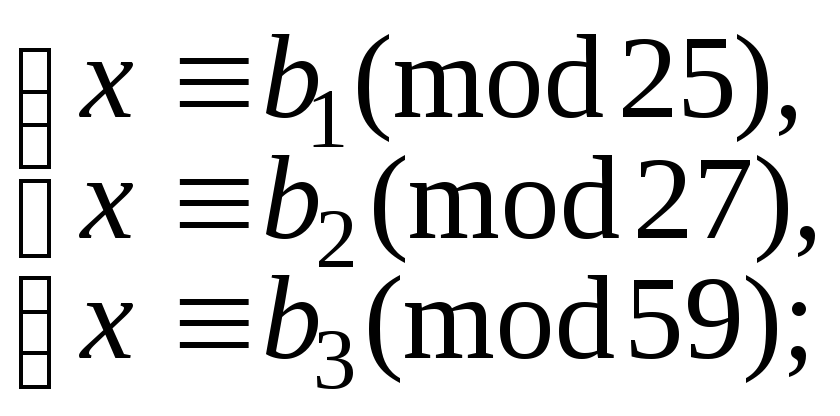
5.9.96. д) 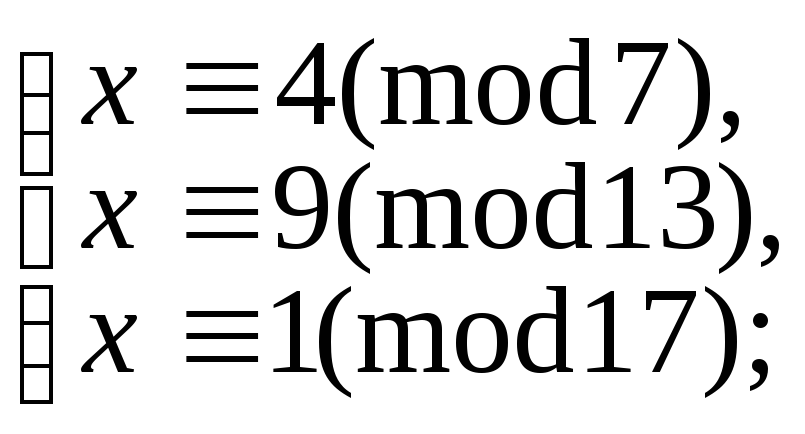5.9.102. л)

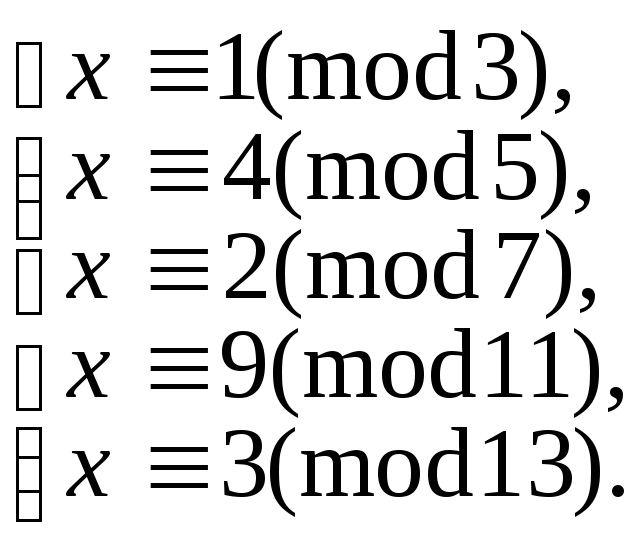
5.9.97. е)

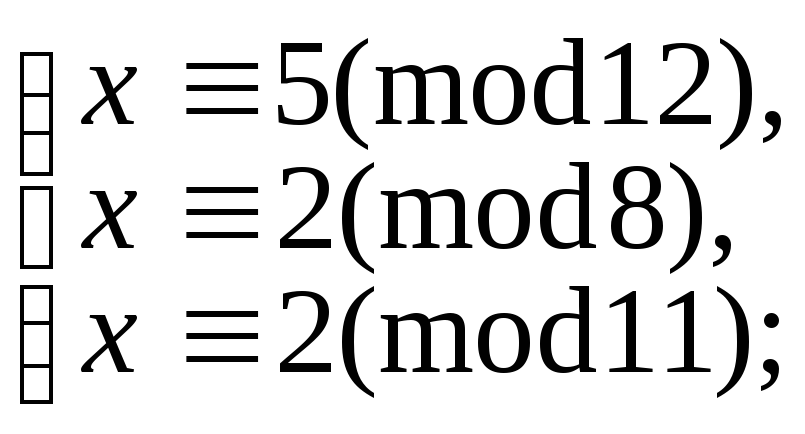
9.12. Розв’язати системи порівнянь:

5.9.103. а) 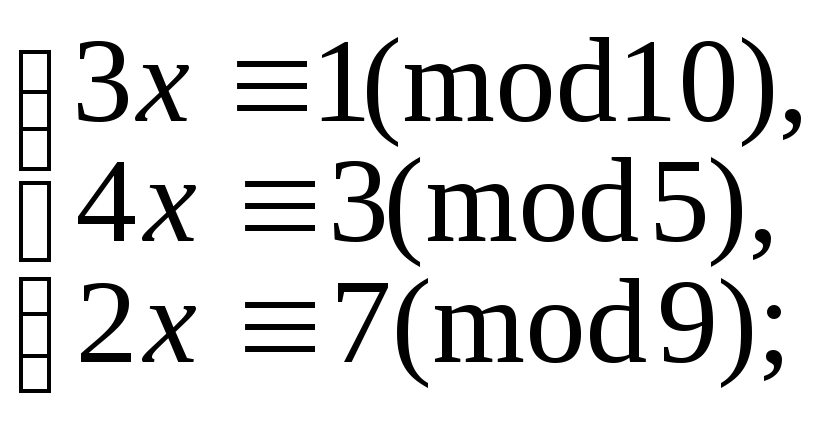5.9.107. д)

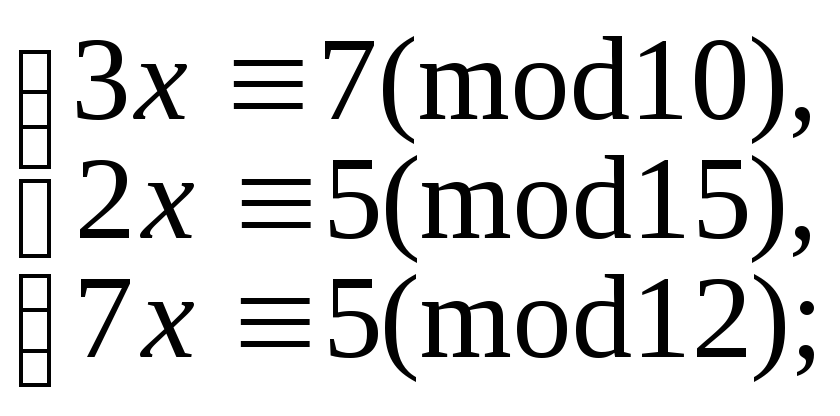
5.9.104. б) 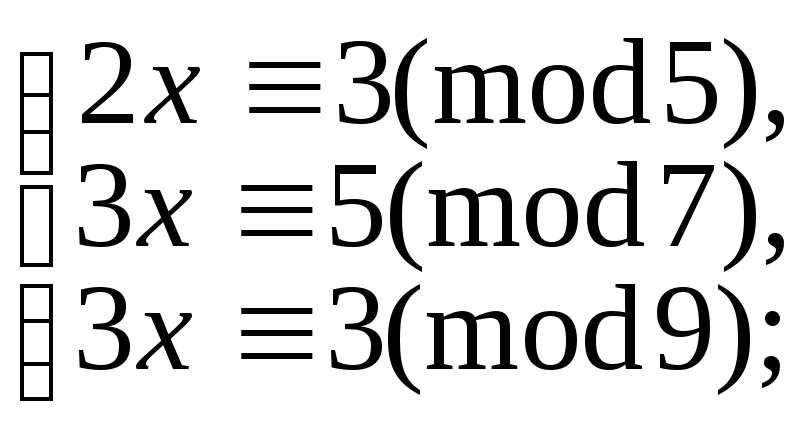5.9.108. е)

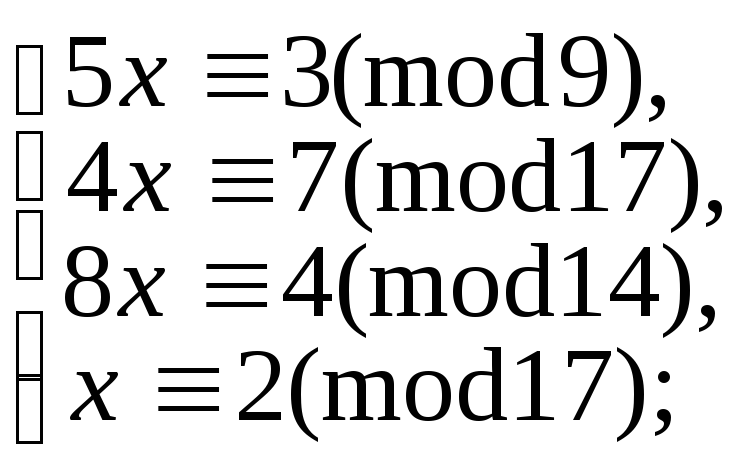
5.9.105. в) 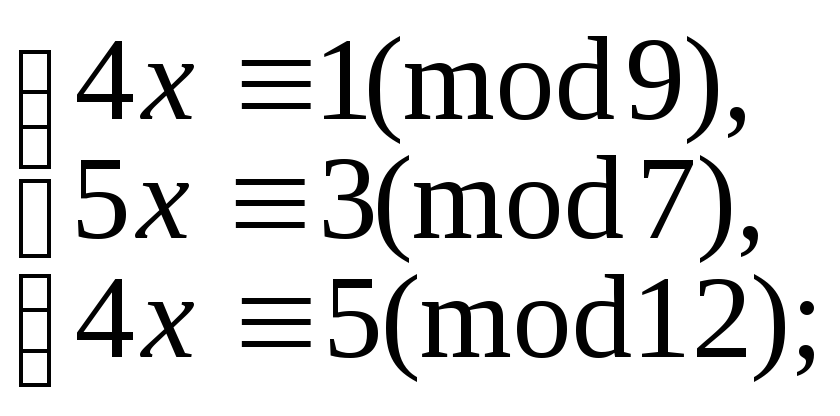5.9.109. є)

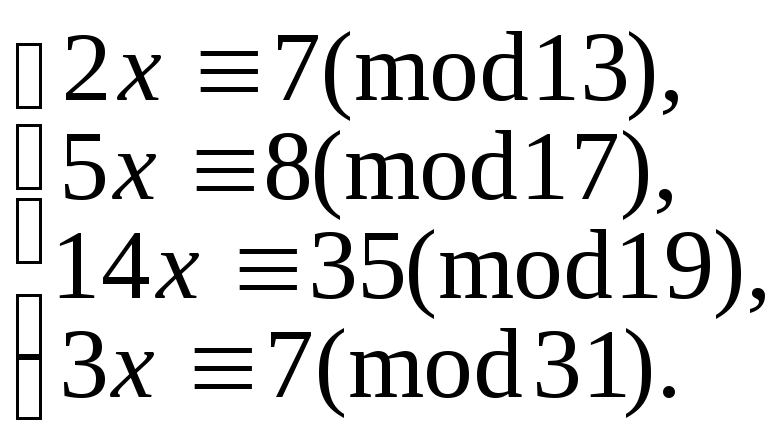
5.9.106. г)

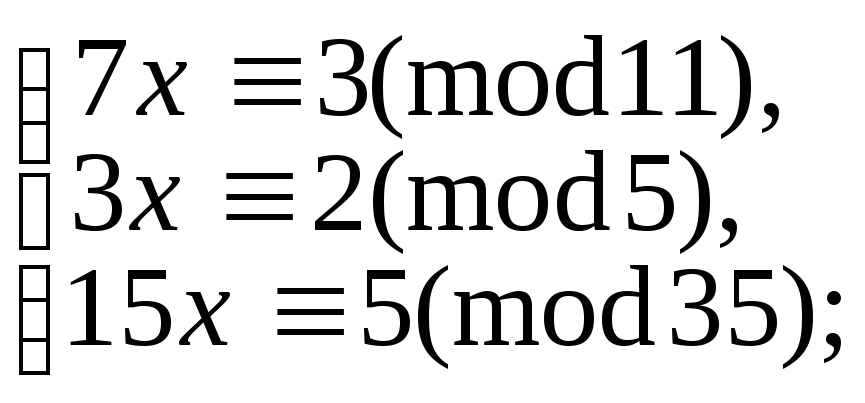
5.9.110. 9.13. Знайти точки з цілими координатами, які лежать на прямих , 2x + 9y = 15 і 5x – 13y = 12 на одному перпендикулярі до осі абсцис.

9.14. При яких значеннях a мають розв’язки такі системи:

5.9.111. а) 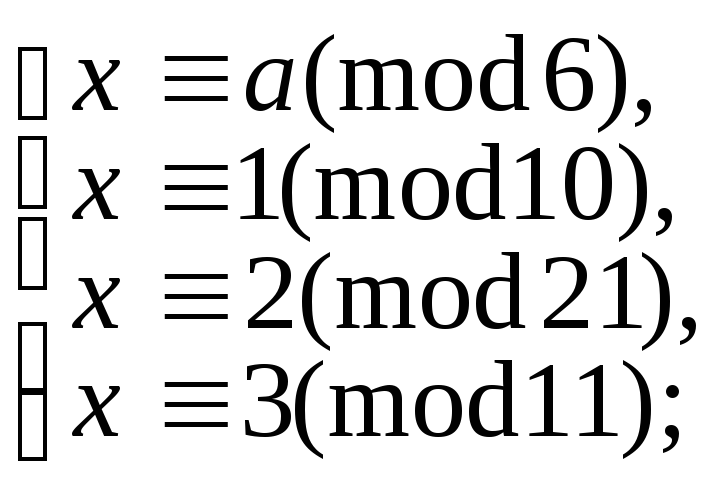5.9.113. в)

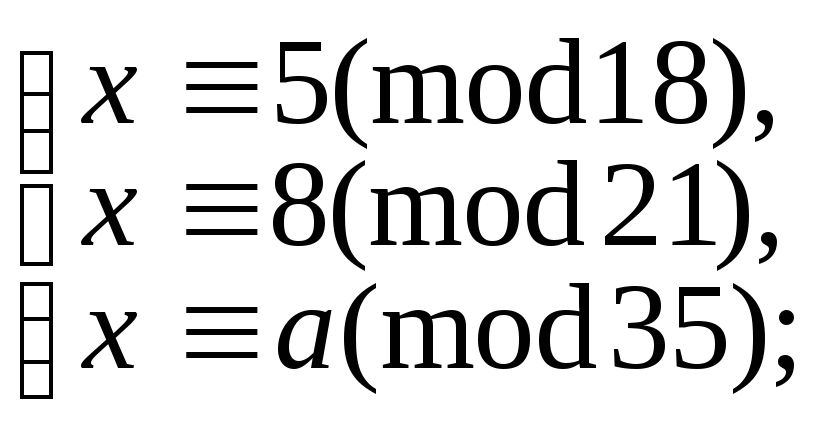
5.9.112. б) 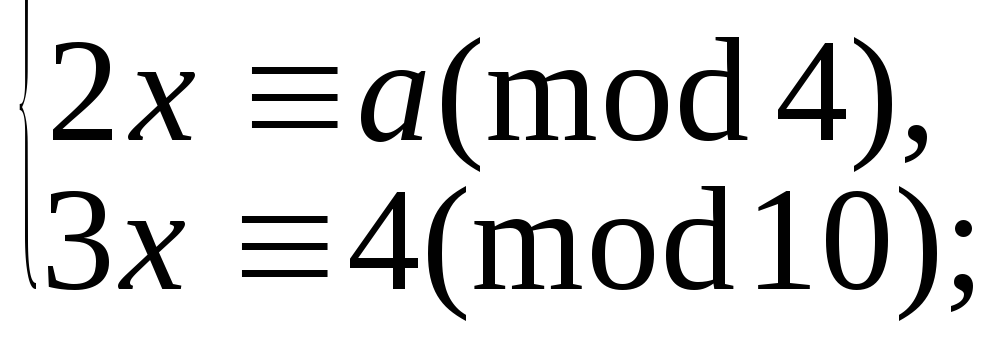5.9.113. г)

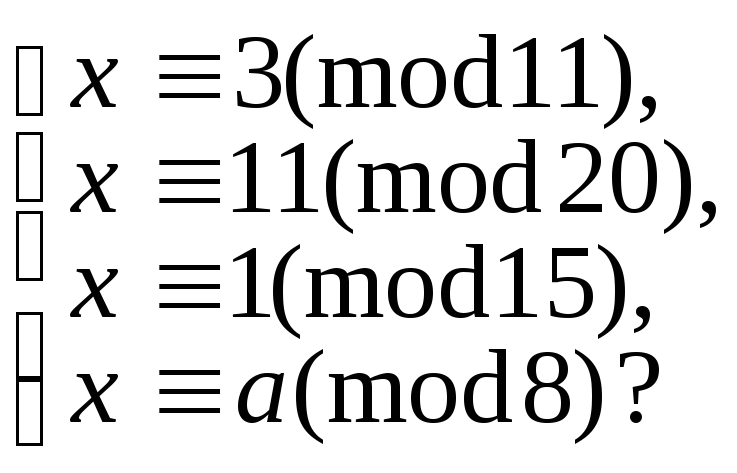
5.9.114. 9.15. Знайти хоча б одне значення m , при якому несумісною є система:

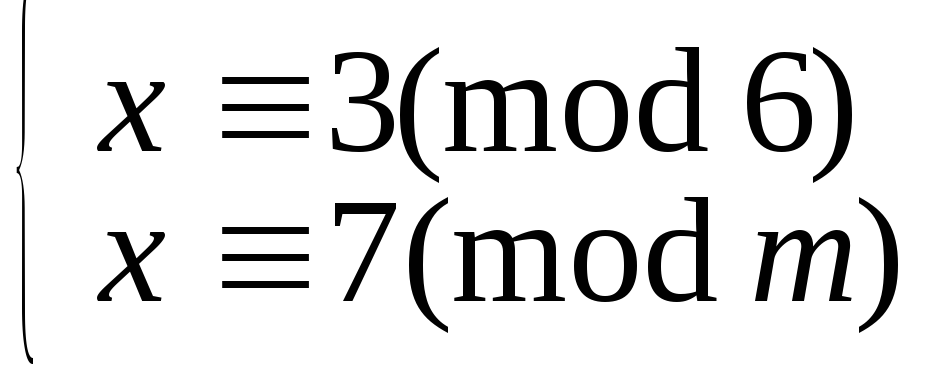
5.9.115. 9.16. Скільки точок з цілими координатами лежать на прямій між прямими x =  100 і x = 150?

5.9.116. 9.17. Довести , що в середині прямокутника, обмеженого прямими , x = 5 і y = 1, y = 2, на прямій 3x – 7y = 1 не має жодної точки з цілими координатами.

14.18. Скільки точок з цілими координатами лежать на заданих прямих між точками з абсцисами a₁ і a₂ :

5.9.117. а) 10x – 11y = 15, a₁ = 30, a₂ = 50;

5.9.118. б) 31x – 47y =23, a₁ = 23, a₂ = 50;

5.9.119. в) 101x – 39y = 89, a₁ = 0, a₂ = 100;

5.9.120. г) 8x – 13y + 6 = 0, a₁ =  100, a₂ = 150;

5.9.121. д) 7x + 29y = 584, a₁ = 20, a₂ = 160;

5.9.122. е) 90x – 74y = 50, a₁ = 100, a₂ = 200?

5.9.123. 9.19. Нехай точки А і В мають цілі координати А(x₁, y₁), B(x₂, y₂). Довести, що на відрізку АВ число внутрішніх точок з цілими координатами дорівнює d 1, де d = (y₁ – y₂, x₁ – x₂).

9.20. Через скільки точок з цілими координатами проходять сторони трикутника з вершинами:

5.9.123. а) А(2, 3), В(7, 8), С(13, 5);

5.9.124. б) А(2, 1), В(20, 7), С(8, 15)?

5.9.125. 9.25. Знайти відстань r між сусідніми точками з цілими координатами, які лежать на прямій ax + by = c, (a, b) = 5.

5.9.126. 9.22. При якій умові дріб можна подати у вигляді суми двох дробів із знаменниками a і b (a, b, c  )?

5.9.127. 9.23. Відгадати день народження, якщо сума добутків числа місяця на 12 і номера місяця на 31 дорівнює 339. У чому суть відгадування?

5.9.128. 9.24. Для первезення зерна є мішки по 60 і 80 кг. Скільки таких мішків потрібно для перевезення 440 кг зерна?

5.9.129. 9.25. На будівництво газопроводу на трасу завдовжки 283 м було доставлено труби, довжина яких 5 і 7 м. Скільки труб доставили?

5.9.130. 9.26. Скільки квитків по 30 і 50 коп. можна купити на 14 крб. 90 коп.?