Технічне завдання

Даний курсовий проект являє собою ескізний проект цифрової системи передачі з ІКМ та містить наступні етапи:

1. Вибір частоти дискретизації телефонних сигналів, розрахунок кількості розрядів у кодовому слові і захищеності від шуму квантування на виходах каналів ЦСП.

2. Розробка структурної схеми прикінцевого устаткування ЦСП.

3. Розробка структури часових циклів первинної ЦСП і розрахунок тактової частоти цифрового сигналу без розрахунку синхронізації. Побудова сигналу на виході регенератора (у коді КВП-3/HDB-3) для заданої кодової послідовності символів.

4. Розрахунок максимальних довжин ділянок регенерації та вибір типу кабелю.

5. Оцінка надійності лінійного тракту ЦСП.

Вихідні дані до курсового проекту наведено в табл. Б.1 додатку Б. Вони визначаються порядковим номером студента у журналі академічної групи.

Зауваження: Завдання і вихідні дані разом з номером варіанта повинні бути наведені у технічному завданні пояснювальної записки.

Методичні вказівки по виконанню курсового проекту

1 Вибір частоти дискретизації телефонних сигналів, розрахунок кількості розрядів у кодовому слові і захищеності від шуму квантування на виходах каналів цсп

1.1 Завдання для виконання розділу 1

Вибрати частоту дискретизації f_Д телефонних сигналів, обґрунтувати вибір. Вибрати й обґрунтувати вибір характеристики компресії. Визначити кількість розрядів у кодовому слові m, необхідну для забезпечення необхідної захищеності гармонічного сигналу від шуму квантування A_З.КВ. у каналах розроблюваної ЦСП у пункті прийому. Для знайденої кількості розрядів розрахувати і побудувати залежність захищеності гармонійного сигналу від шуму квантування в пункті прийому як функції рівня цього сигналу. Під час розрахунку прийняти, що рівень перевантаження кодера складає 0 дБ. Визначити діапазон зміни рівня вхідного сигналу (у дБ), у якому захищеність від шуму квантування на прийомі залишається не нижче заданої в табл. Б1.

1.2 Методичні вказівки по виконанню завдання

Вибір частоти дискретизації f_Д здійснюють на основі теореми В.А. Котельникова. У тексті пояснювальної записки треба обґрунтувати вибір номіналу частоти дискретизації, навести спектральну діаграму АІМ сигналу і вказати на ній розрахункові значення частот.

Розрахунок кількості розрядів у кодовому слові m виконують на основі заданої величини захищеності від шуму квантування на виході каналу A_З.КВ. і кількості переприйомів по ТЧ n. Згадайте, у чому суть операції квантування, що таке рівномірне і нерівномірне квантування. Обґрунтуйте, чому в системах з ІКМ і ЧРК, призначених для передачі телефонних сигналів, треба застосовувати нерівномірне квантування з характеристикою компресії, близькою до логарифмічної.

Вибір частоти дискретизації здійснюється на основі теореми В.А. Котельникова, згідно з якою неперервний сигнал u(t), що має спектр S(ω), обмежений частотою ω_в = 2πF_в, цілком визначається відліками його миттєвих значень u(k∙t), що відстоять друг від друга на інтервали Δt ≤ 1 / (2F_в). Доведення цієї теореми засновано на розкладанні функції в ряд виду:

. (1.1)

Імпульсна послідовність, отримана в результаті дискретизації, являє собою АІМ сигнал, закон зміни амплітуди якого відповідає вихідному коливанню.

Розглянемо вимоги, що висуваються до вибору частоти дискретизації, з точки зору можливості виділення первинного сигналу при прийомі за рахунок використання фільтрації низькочастотної частини спектра. На рис. 1.1 а зображений спектр первинного сигналу, а на рис. 1.1 б-г – спектри S_В(ω) при різних співвідношеннях між ω_В і ω_Д. Якщо відповідно до теореми Котельникова обрано ω_Д = 2 ω_в, спектр дискретизованого сигналу має вигляд, показаний на рис. 1.1 6. Частина спектра, що повинна бути відфільтрована, на рисунку заштрихована. Видно, що при ω_Д = 2·ω_в частоти ω_в і (ω_Д - ω_в) збігаються, і спектр первинного сигналу може бути відокремлений від нижньої бічної смуги АІМ сигналу, що лежить у діапазоні від (ω_Д - ω_в) до ω_д, тільки за допомогою ФНЧ з ідеальною АЧХ. Такий фільтр, як відомо, реалізувати фізично неможливо. Тому на практиці вибирають ω_Д > 2·ω_в (рис. 1.1 в). У цьому випадку спектри в смугах частот 0ω_в і (ω_Д - ω_в) ω_д рознесені, і можна виділити первинний сигнал реальним фільтром. При дискретизації телефонного сигналу зі спектром 0,33,4 кГц частоту дискретизації вибирають рівною 8 кГц. При ω_Д < 2ω_в спектри вихідного сигналу перекриваються (рис. 1 (г)), і їхнє розмежування неможливе.

Отриманий у результаті часової дискретизації АІМ сигнал є неперервним за рівнем. Для перетворення його в дискретний сигнал необхідно здійснити операцію квантування.

У курсовому проекті необхідно обчислити частоту дискретизації.

Згідно з рекомендацією МСЕ частота дискретизації вибирається з умови:

f_Д = (2,2 ... 2,4)·F_В, (1.2)

де F_В – верхня частота вихідного сигналу; F_В = 3,4 кГц.

f_Д = 2,35·3,4 = 8 кГц;

Т_д = 1 / f_Д = 1 / 8·10 ³ = 0,125·10 ^{- 3} сек = 125 мксек.

При квантуванні сигналів відстань між найближчими дозволеними рівнями називається кроком квантування. Шкала квантування називається рівномірною, якщо всі кроки квантування однакові, і нерівномірною, якщо крок квантування по шкалі непостійний.

Квантування сигналів супроводжується певною похибкою, яка тим менша, чим менший крок квантування.

При рівномірному квантуванні захищеність від шумів квантування мала для слабких сигналів і збільшується з ростом рівня сигналу. Тому, якщо вибрати інтервал квантування, що забезпечує необхідну захищеність для слабких сигналів, то для великих сигналів ця захищеність виявиться невиправдано великою. Крім того, при рівномірному квантуванні і забезпеченні необхідної захищеності для слабких сигналів число рівнів квантування різко зросте.

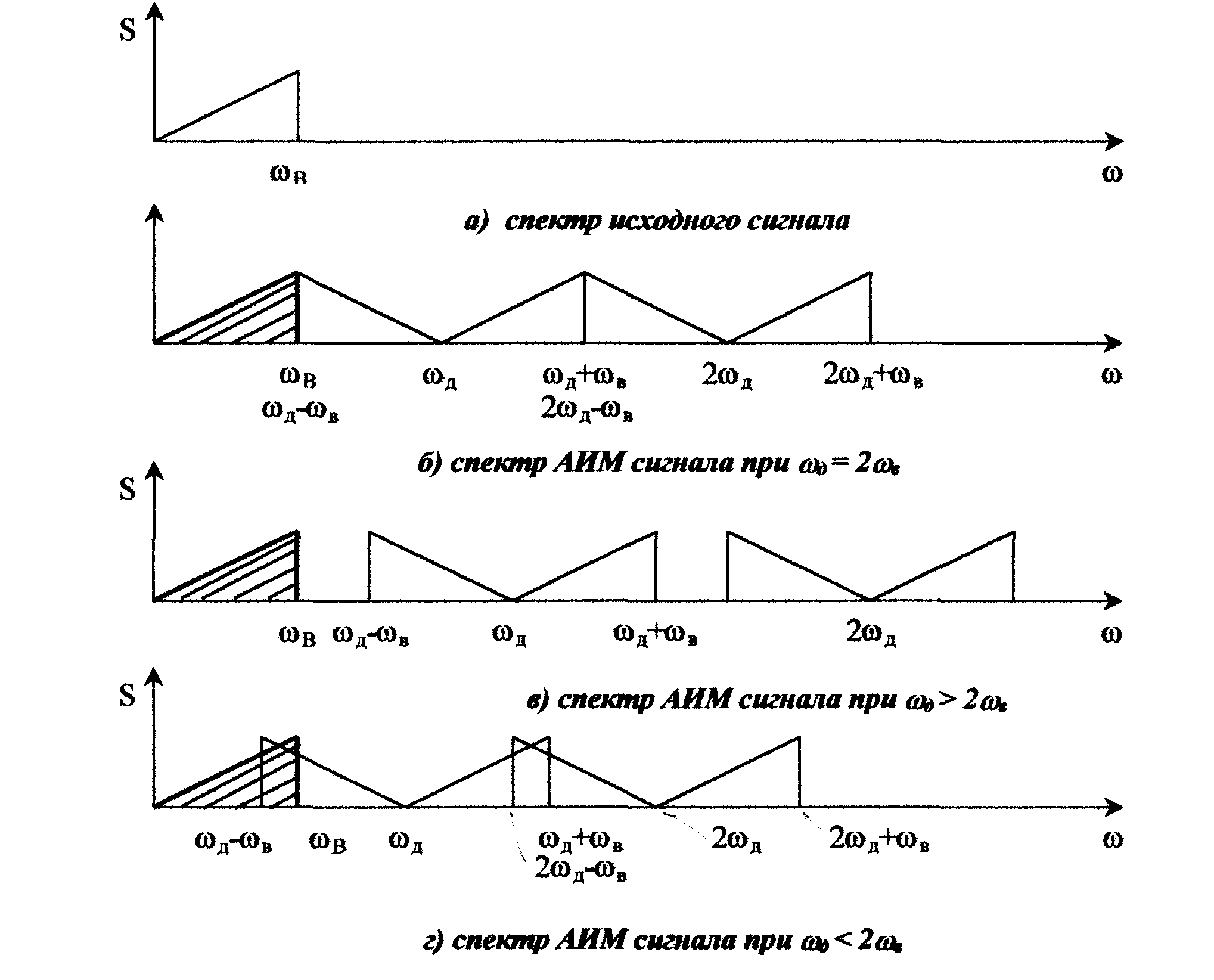
Рисунок 1.1 – Вплив частоти дискретизації на можливість відновлення сигналу за допомогою фільтру

Число рівнів квантування N_кв однозначно пов'язане з числом розрядів m:

N_кв = 2 ^m. (1.3)

Для забезпечення захищеності в 30 дБ число рівнів квантування повинно дорівнювати 4096, а число розрядів кодової комбінації дорівнює 12. Це ускладнює устаткування, тому від кодування з рівномірним квантуванням переходять до кодування з нерівномірним квантуванням.

Сутність нерівномірного квантування полягає в тому, що для слабких сигналів інтервал квантування обирається малим, таким, щоб забезпечити необхідну захищеність, а для великих сигналів інтервал квантування обирається досить великим, щоб забезпечити захищеність таку ж, як і для слабких сигналів. Необхідно намагатися, щоб захищеність залишалася постійною для будь-яких значень рівня сигналу. Нерівномірне квантування приводить до зменшення числа рівнів квантування, а отже, дозволяє зменшити число розрядів кодової комбінації. Необхідної захищеності можна досягти при 8-розрядній кодовій комбінації.

Технічно реалізувати нерівномірне квантування доволі складно. Тому використовується ідея, за допомогою якої забезпечується сталість захищеності для сигналів. З цією метою стискається динамічний діапазон сигналу на передавальному боці. Це досягається шляхом реалізації сегментарної амплітудної характеристики (табл. 1.1). А далі здійснюється рівномірне квантування.

Таблиця 1.1 – Параметри сегментарної амплітудної характеристики

Номер сегменту	Розмір кроку квантування	Верхня межа сегменту
7	64·Δ	U0
6	32·Δ	U0 / 2
5	16·Δ	U0 / 4
4	8·Δ	U0 / 8
3	4·Δ	U0 / 16
2	2·Δ	U0 / 32
1	1·Δ	U0 / 64
0	1·Δ	U0 / 128

де U₀ - рівень перевантаження в у.о.; Δ - крок дискретизації в у.о.

Поряд з логарифмічними характеристиками компресії типу μ у системах з ІКМ велике поширення одержали логарифмічні характеристики компресії типу А (А = 87,6 / 13), вони описуються виразами:

(1.4)

де x = U_ВХ/U₀; U_ВХ – амплітуда відліку аналогового сигналу.

Такий закон компресії називають А - законом. Абсолютне значення відношення сигнал-шум при А и μ законі приблизно рівні, якщо А обрано рівним μ.

Рекомендується застосовувати компресію, засновану на 16 - сегментній характеристиці, що відповідає А - закону (А = 87,6 / 13). У цьому випадку весь динамічний діапазон поділяють на 16 відрізків (сегментів) - по вісім для кожної полярності. У межах кожного сегменту крок квантування незмінний, а при переході до наступного сегменту подвоюється. Оскільки характеристика компресії є непарною функцією, звичайно розглядають її позитивну гілку.

Відносний рівень сигналу обчислюється як

р = 20·ℓg (U_ВХ/U₀). (1.5)

Максимум захищеності в діапазоні рівнів -∞ ≤ р ≤ –36 дБ досягається при р = 20·ℓg (1/64) ≈ - 36 дБ і складає

= 6·m - 10, дБ, (1.6)

де m - кількість розрядів у кодовому слові.

При –36 дБ ≤ р ≤ 0 захищеність від помилки квантування змінюється несуттєво, оскільки при збільшенні рівня сигналу збільшуються і похибки квантування (за рахунок збільшення кроку). При р > 0 настає перевантаження кодера і захищеність різко спадає.

Мінімальна величина захищеності нижче, ніж розрахована по формулі (1.6), приблизно на 2 дБ; окрім того, слід врахувати апаратурні похибки, які зазвичай становлять 4 ... 5 дБ. Таким чином, мінімальну величину захищеності від помилок квантування при нерівномірному квантуванні з характеристикою А в діапазоні рівнів –36 дБ ≤ р ≤ 0 можна оцінити наступним чином:

≈ 6 · m – (16 ... 17), дБ. (1.7)

Якщо в ЦСП, що розробляється, передбачені переприйоми по ТЧ, то захищеність на виході будь-якого з каналів буде меншою за розраховану по формулі (1.7). Зазвичай вважають, що помилки квантування, що вносяться при кожному переприйомі, не корельовані і тому сумуються за законом додавання потужностей. Отже,

= 6 · m – (16 ... 17) – 10 · ℓg (n + 1), дБ, (1.8)

де n – кількість переприйомів по ТЧ.

Звідси випливає формула для визначення кількості розрядів у кодовому слові:

m = Ц {[ + 10 · ℓg (n + 1) + (16 ... 17)] / 6}, (1.9)

де Ц - найближче ціле число, більше за число, яке стоїть у фігурних дужках.

Нехай m = 8, n = 2. Визначаємо за формулою (1.8) мінімальну величину захищеності сигналу в пункті прийому у діапазоні рівнів –36 дБ ≤ р ≤ 0 дБ:

= 6 · m – (16 ... 17) – 10 · ℓg (n + 1) = 48 - 16 - 10 · ℓg 3 ≈ 27 дБ.

Максимальна величина захищеності у тому ж діапазоні буде приблизно на З дБ більше за мінімальну

= + 3 = 27 + 3 = 30 дБ.

Креслимо на графіку горизонтальні прямі, що відповідають розрахованим і (рис.1.2). Захищеність при р = - 36 дБ приблизно на 2 дБ вище, ніж

= + 2 = 27 + 2 = 29 дБ.

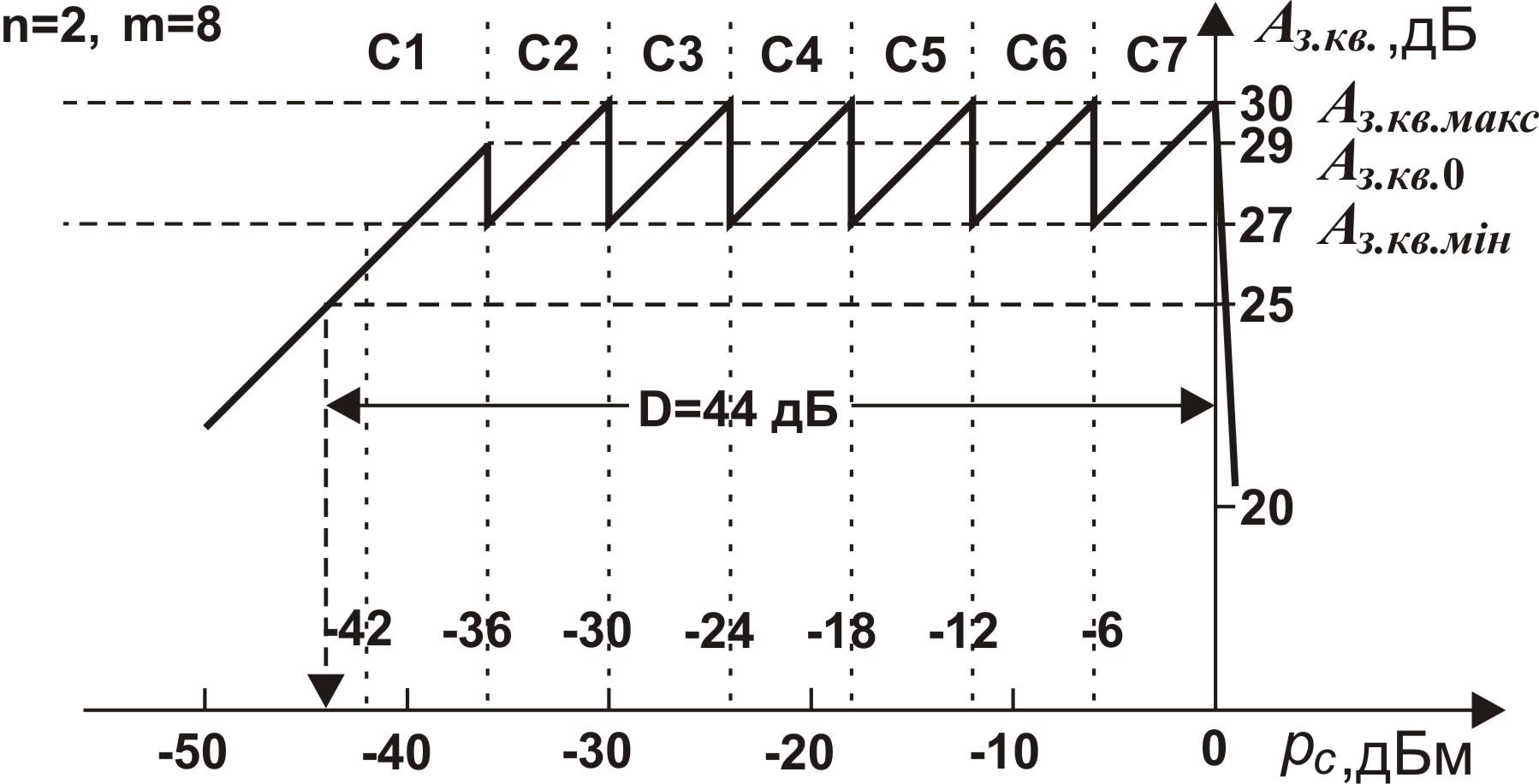
Рисунок 1.2 – Залежність захищеності від шуму квантування від рівня сигналу

Значення захищеності від шуму квантування в діапазоні рівнів - 36 ≤ p ≤ 0 дБ лежать між цими прямими. У діапазоні - ∞ < р ≤ - 72 дБ рівень шуму квантування дорівнює рівню сигналу, і захищеність дорівнює 0. У діапазоні - 72 ≤ p ≤ - 36 дБ квантування є рівномірним, і тому зменшується на 1 дБ при зменшенні рівня сигналу на таку ж величину. При p > 0 настає перевантаження кодеру і захищеність різко спадає.

Діапазон зміни рівня сигналу, у якому захищеність залишається не нижче ніж завада, знаходять безпосередньо з рис.1.2. При = 25 дБ він складає D = 44 дБ.