10

Міністерство освіти і науки України

Національний університет “Львівська політехніка”

Синтез сигналів за фур’є Методичні вказівки до лабораторної роботи № 4

з предмету “Сигнали та процеси в радіоелектроніці”,

для студентів базового напряму “Радіотехніка”

Затверджено

на засіданні кафедри

“Теоретична радіотехніка

та радіовимірювання”

Протокол № 6 від 26 березня 2010 р.

Львів - 2010

Синтез сигналів за Фур’є. Методичні вказівки до лабораторної роботи №4 з предмету “Сигнали та процеси в радіоелектроніці” для студентів базового напряму “Радіотехніка” /Упорядники: Желяк Р.І., Мелень М.В.- Львів: НУ ЛП, 2010. - с. 10.

Упорядники: Желяк Р.І., проф., канд. техн. наук,

Мелень м.В., доц., канд. Техн. Наук.

Рецензенти: Волочій Б.Ю., проф., докт. техн. наук,

Бондарєв А.П., проф., докт. техн. наук.

Відповідальний за випуск: Надобко О.В., доц., канд. техн. наук.

© Желяк Р.І., Мелень М.В., 2010

1. Мета роботи

Метою роботи е вивчення методів аналізу і синтезу складних сигналів за допомогою систем ортогональних елементарних гармонічних функцій.

2. Основні положення

З математики відомо, що довільну складну функцію завжди можна подати у вигляді суми простих (елементарних) функцій , тобто подати її у вигляді узагальненого ряду Фур’є:

, (1)

де - коефіцієнти узагальненого ряду Фур’є – значення проекцій складної функції на координатні осі багатовимірного простору, що задаються простими елементарними функціями .

З (1) випливає, що будь який складний сигнал можна точно описати безмежною сумою зважених ортогональних елементарних сигналів , тобто розкласти його в узагальнений ряд Фур’є. Проте при практичному розв’язку багатьох інженерних задач замість ряду (1) використовують вкорочений ряд Фур’є:

, (2)

який описує заданий сигнал з деякою допустимою похибкою, середньоквадратичне значення якої залежить від числа врахованих коефіцієнтів ряду N і оцінюється виразом:

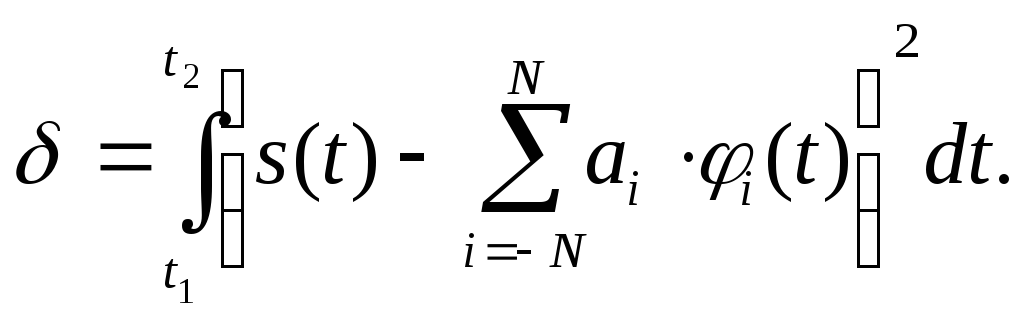(3)

Величина  називається середньою квадратичною похибкою апроксимації (подання) рядом заданого сигналу s(t).

Якщо для неперервного сигналу можна вибрати a_i так, щоб при збільшенні кількості членів ряду величина  ставала достатньо малою, то сукупність ортого-нальних функцій {f_i (t)} називається повною, а ряд (2) в цьому випадку називається збіжним в середньому.

В загальному випадку елементарні функції можуть бути довільними, проте, якщо потрібно забезпечити умову взаємної незалежності значень коефіці-єнтів узагальненого ряду Фур’є, елементарні функції повинні задовольняти умову ортогональності на деякому відрізку часу (t₁, t₂):

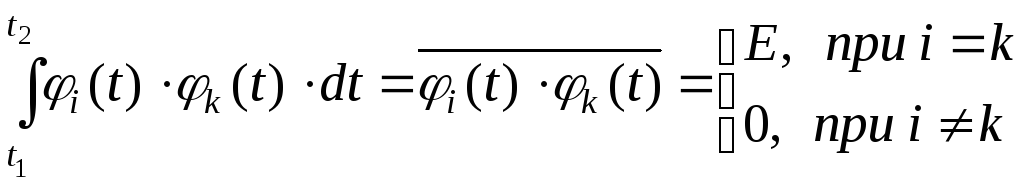, (4)

де

У цьому випадку сукупність функцій називають системою ортогональних функцій на відрізку (t₁, t₂).

Якщо при цьому додатково виконується умова

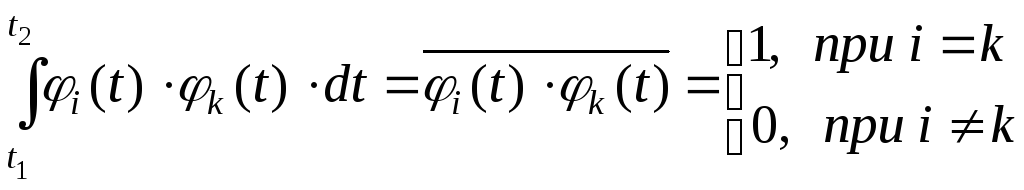, (5)

то систему елементарних функцій {} називають ортонормованою.

В даному випадку, для періодичних сигналів (n – довільне ціле число; Т – період повторення) елементарні функції повинні задовольняти умову періодичності .

Неважко довести, що використання при розкладі сигналу в ряд (1) елементарних ортогональних або ортонормованих функцій дозволяє одноз-начно визначати коефіцієнти а_і ряду у вибраному координатному базисі:

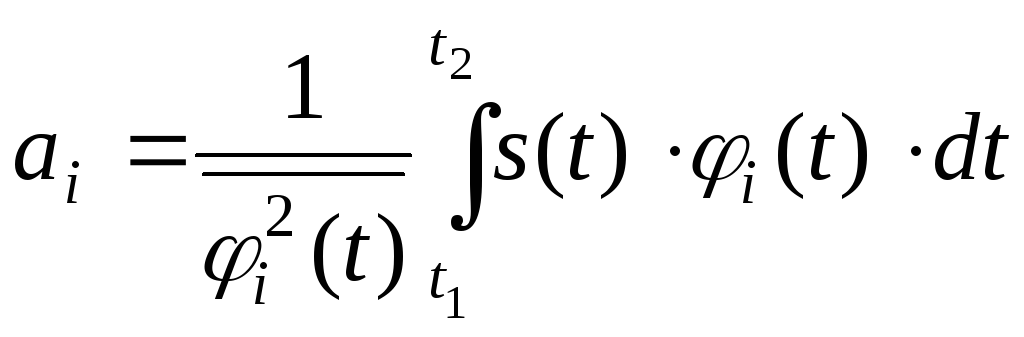. (6)

Аналіз показує, що визначення коефіцієнтів ряду а_і за формулою (4) забезпечує мінімальну середню квадратичну похибку апроксимації сигналу рядом (1) або (2).

Вибір виду ортогональних функцій, за якими проводиться розклад складного сигналу на суму елементарних сигналів залежить від форми і властивостей склад-ного сигналу. Так для періодичних сигналів, миттєве значення яких монотонно змінюється в часі, найчастіше використовується система гармонічних функцій з кратними аргументами ( і (або) , ) та система експоненціальних функцій з кратними комплексними аргументами (, ).

У цьому випадку сигнал може бути поданий рядом:

або

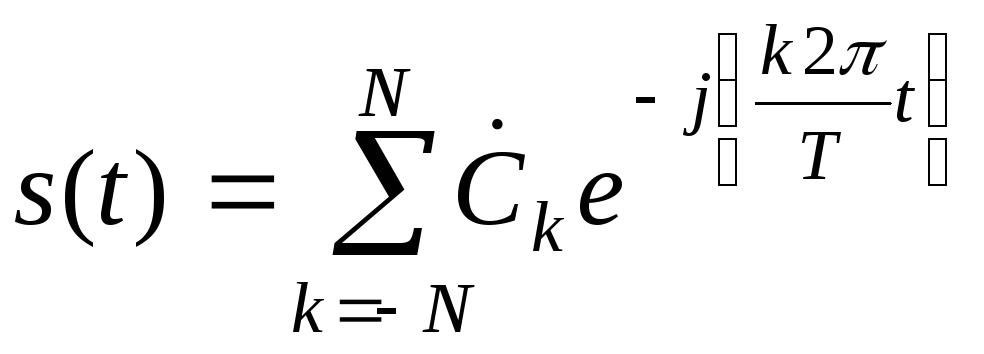, (7)

в яких коефіцієнти , , та розраховуються за допомогою формул:

; ; ; (8)

; ; .

Ряд (7) подає коливання у вигляді суми постійної складової (, або ), та гармонічних коливань (з амплітудами , , і початковими фазами ) з кратними частотами, які називають гармоніками. Найнижчу частоту коливань має перша (основна) гармоніка. Її значення визначається періодом повторення сигналу - .

Н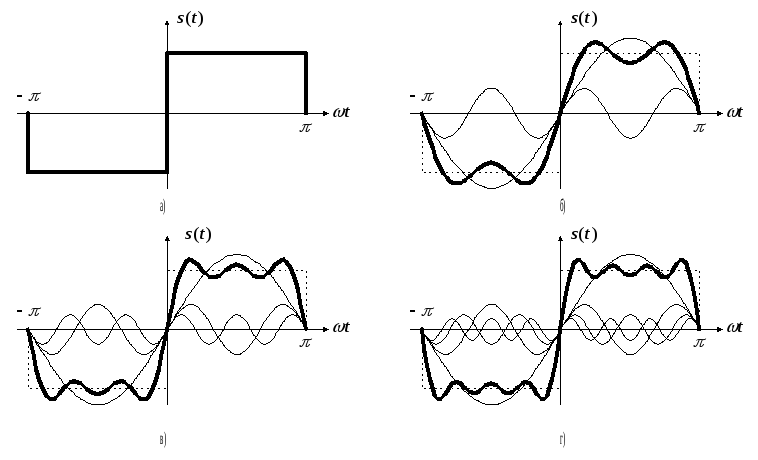 а рис. 1, б, в, г штриховими лініями показані часові залежності окремих гар-монічних складових з кратними частотами, а суцільними лініями - результат сумування цих гармонік (на рис. 1, б – сума першої і третьої гармонік, на рис. 1, в сума доповнена п’ятою, а на рис. 1, г - сьомою гармоніками).

Рис. 1. Часові залежності періодичної послідовності прямокутних імпульсів –а) та суми вкороченого ряду Фур’є для k=3 – б); k=5 – в); та k=7 – г).

З поданих рисунків випливає, що із збільшенням кількості гармонік сума ряду наближається до заданого сигналу усюди, крім точок розриву сигналу , де утворюється викид. При величина цього викиду лише на 18% відрізняється

від заданого сигналу. Згаданий дефект збіжності ряду в математиці отримав назву “явище Гібса”. Зауважимо, що при відсутності стрибкоподібних змін ряд Фур’є швидко збігається до в усіх точках.

Доцільно відзначити, що подібним способом можна синтезувати і сигнали з різними видами модуляції. У цьому випадку потрібно сумувати гармонічні сигнали з частотами, з яких складається відповідний сигнал. Наприклад, для синтезу сигналу з однотональною амплітудною модуляцією потрібно просумувати три гармонічних коливання з частотами f₀ - , f₀ та f₀ + . Для синтезу сигналу з однотональною односмуговою амплітудною модуляцією потрібно просумувати два гармонічних коливання з частотами f₀ та f₀ +  або f₀ -  та f₀. Для синтезу сигналу з однотональною балансною амплітудною модуляцією потрібно просумувати два гармонічних коливання з частотами f₀ +  та f₀ - .