2.4. Пример выполнения задания 5
В
пространстве даны точки А(2;
0; 1), В(2; 1; 1), С(4; 1;
3), S(1;
1; 0). Сделаем схематично чертеж пирамиды
А
а)
длину ребра АВ можно найти как длину
вектора
.
Т.к.
,
то
.
Уравнения ребра найдем как уравнения прямой, проходящей через две заданные точки
.
В нашем случае
,
канонические
уравнения ребра АВ.
Замечание: форма записи канонических уравнений прямой является условной и в ней не деление на ноль, а отношение.
б)
грань АВС образована векторами
и
,
причем
.
Найдем векторное произведение этих векторов
(такой определитель лучше вычислять разложением по элементам первой строки).
Используя геометрическое свойство векторного произведения, получаем площадь грани АВС
.
В
качестве нормального вектора
плоскости АВС можно взять векторное
произведение
,
но лучше предварительно его сократить
на 2, т.е. получаем
.
Уравнение плоскости АВС найдем как
уравнение плоскости, проходящей через
заданную точку
перпендикулярно заданному вектору
:
.
В качестве точки М0 можно взять любую из точек плоскости АВС, например точку А, тогда получаем
общее
уравнение плоскости АВС.
в)
длину высоты SH
можно найти как расстояние от точки S
до плоскости АВС. Для этого общее
уравнение плоскости
приведем к нормальному виду. Т.к.
нормальный вектор плоскости,
его
длина,
нормальное
уравнение плоскости.
Подставим координаты точки S(1; 1; 0) в полученное уравнение и возьмем модуль полученного числа
.
Так
как
нормальный вектор плоскости АВС, то он
является направляющим вектором высоты
SH
и уравнения высоты можно найти как
уравнения прямой, проходящей через
заданную точку
параллельно заданному вектору
:
.
В нашем случае
канонические
уравнения высоты SH.
г) проекцией вершины S на плоскость АВС является точка Н, которую можно найти как точку пересечения плоскости АВС и прямой SH. Для этого канонические уравнения прямой SH приведем к параметрическим уравнениям
,
Подставим эти уравнения в уравнение плоскости АВС
Полученное значение t подставим в параметрические уравнения
т.е.
д) проекцией ребра АS на грань АВС является прямая АН, уравнения которой можно найти как уравнения прямой проходящей через две заданные точки:
.
Т.к. проекция проходит через точки А и Н, то ее уравнения имеют вид
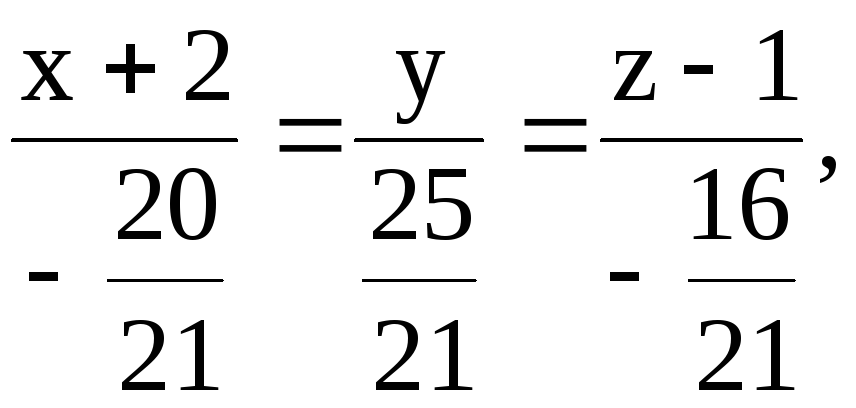
канонические
уравнения проекции.
е)
уравнения искомой прямой можно найти
как уравнение прямой, проходящей через
заданную точку
параллельно заданному вектору
т.е.
.
В нашем случае получаем
ж)
вектор
является нормальным вектором искомой
плоскости. Уравнение этой плоскости
можно найти как уравнение плоскости,
проходящей через заданную точку
перпендикулярно заданному вектору
:
.
В нашем случае
з)
угол
между ребрами АВ и AS
можно найти как угол между векторами
и
:
Т.к.
,
,
то
и)
Т.к. угол
между прямой
и плоскостью
находится по формуле
и
направляющий вектор прямой AS;
нормальный
вектор плоскости АВС, то
к)
найдем нормальный вектор
плоскости АВS
Т.к.
,
то
нормальный
вектор плоскости АВС.
Угол
между плоскостями можно найти как угол
между их нормальными векторами
,
,
т.е.
В нашем случае
Получили
,
т.е. полученный угол
тупой. Две плоскости при пересечении
образуют четыре угла
два тупых
и два острых 1,
причем
,
отсюда для острого угла 1
получаем
.
л) координаты центра тяжести О пирамиды АВСS можно найти как среднее арифметическое соответствующих координат вершин пирамиды, т.е.
т.е.
центр тяжести пирамиды.
м) Т.к. объем пирамиды можно вычислить по формуле
,
причем
площадь основания,
высота
пирамиды.
Получаем
