2.5.2. Решение прямой задачи для функции многих переменных

Рассмотрим задачу определения предельного значения абсолютной погрешности функции f(x ) = f(x₁, x₂,..., x_n), зависящей от n переменных x₁, x₂,..., x_n, определенных на вещественной оси R.

Допустим, аргумент функции задан с погрешностью в точке х=а = (а₁, а₂,..., а_n) приближенным значением х=а* = (а₁*, а₂*,..., а_n*). По каждой переменной x_i ( i = 1,...,n) введем абсолютную погрешность: (а_i^) =а_i - а_i*. Найдем оценки для предельной абсолютной погрешности f(а^ ) значения функции f(x ) в точкех=а, вызванную ошибкой задания ее аргумента.

По аналогии с функцией одной переменной к функции f(x ) применим на параллелепипеде Р, образованном декартовым произведением отрезков [а₁, а₁*],[а₂, а₂*],...,[а_n, а_n*] (Р = [а₁, а₁*][а₂, а₂*]...[а_n, а_n*]), формулу конечных приращений Лагранжа о среднем значении, которая утверждает, что если функция f непрерывна на множестве Р и дифференцируема внутри Р, то внутри Р всегда найдётся такая средняя точкаb параллелепипеда (b  Р), для которой выполняется равенство:

(f(а*) - f(а)) = ((f(x ))/x₁)_{x =b} (а*₁ - а₁) + ((f(x ))/x₂)_{x =b} (а*₂ - а₂) + … + ((f(x ))/x_n)_{x =b} (а*_n - а_n). (2.16)

Геометрический смысл точкиb аналогичен одномерному случаю. В ней проекции касательной плоскости на оси наклонены под теми же углами, что и соответствующие диагонали на гранях Р. Применяя аналогичный вывод и обозначая через max((f(x ))/x_i) максимальное значение частной производной от функции f(x ) по переменной x_i на параллелепипеде Р, получим уточненную оценку для абсолютной погрешности функции f(а^ ) в зависимости от абсолютных погрешностей переменных x₁, x₂,..., x_n:

f(а^)=(f(а*) - f(а)) max(f(x))/x₁  (а₁^) + max(f(x))/x₂(а₂^) +…+ max(f(x))/x_n(а_n^) = f(а^) _ут. (2.17)

Приближенная оценка для абсолютной погрешности функции f(а^ ) в зависимости от абсолютной погрешности переменных x₁, x₂,..., x_n, полученная при условии а₁* а₁, а₂* а₂,..., а_n*а_n, равна:

f(а^)(f(x))/x₁)_{x =а}(а₁^)+(f(x))/x₂)_{x =а} (а₂^) +…+

(f(x))/x_n)_{x =а} (а_n^)= f(а^) _пр. (2.18)

Приближенная (f(а^) _пр) оценка для относительной погрешности функции f(а^ ) в зависимости от относительных погрешностей переменных x₁, x₂,..., x_n будет следующей:

(f(а))=(f(а))/f(а)(lnf(x))/x₁)_{x =а}x₁^ (а₁^)+

(lnf(x))/x₂)_{x =а} x₂^(а₂^) +…+(lnf(x))/x_n)_{x =а} x_n^ (а_n^) = f(а^) _пр.. (2.19)

Пример 2. Оценить для точки на эллипсоиде, заданном формулой

приближенные значения предельных абсолютной погрешности ( z)_пр и относительной погрешности ( z)_пр положения точки на эллипсе по координате z при заданных значениях координат x=3, у=2 и их абсолютных погрешностях (x) = 0,1 и (у) = 0,2.

Решение. Выразим зависимость z(x,y) и определим z(3,2):

Общий вид частных производных функции z(x,y) по переменным x,y, их абсолютные значения в точке (3,2):

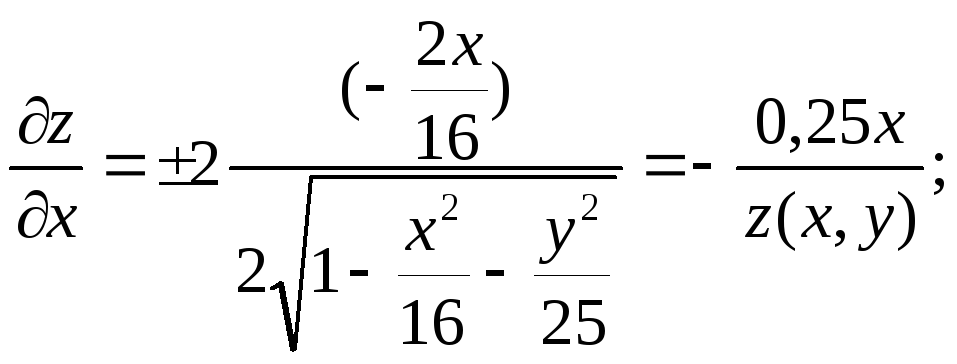
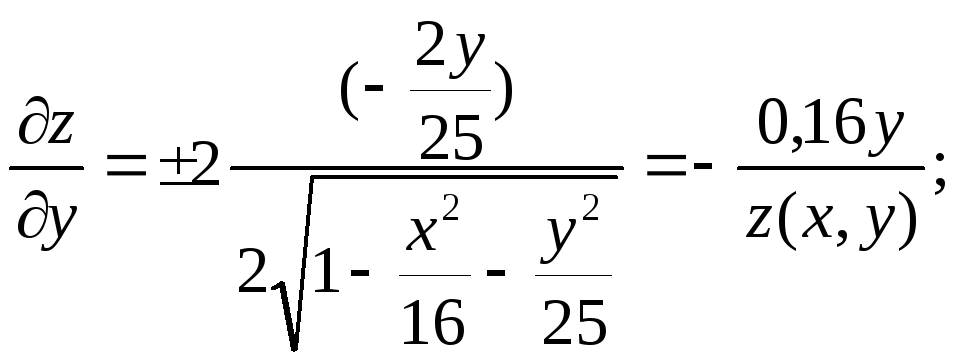
Приближенную оценку для абсолютной погрешности функции z(x,y) получаем из (2.18): z(x,y)  0,1054 0,1 +0,3040,2 = 0,0713.

Приближенную оценку для относительной погрешности функции z(x,y) при известной оценке z(x,y) проще получить, используя определение относительной погрешности: z(x,y) = z(x,y) / z(x,y) = 0,0713/1,054 = 0,0677.