2.5. Погрешность функции. Прямая и обратная задачи теории погрешностей

Основная (прямая) задача теории погрешностей заключается в следующем: по известным значениям погрешностей исходных данных определить погрешность некоторой функции от этих величин. В обратной задаче задается погрешность функции и требуется найти обеспечивающие ее погрешности переменных функции.

2.5.1. Решение прямой задачи для функции одной переменной

Вначале рассмотрим функцию одной переменной f(x), определенную на вещественной оси R. Допустим, аргумент функции задан с погрешностью в точке х=а приближенным значением х=а*. Абсолютная погрешность задания аргумента: (а^) =а - а*. Необходимо найти предельную абсолютную погрешность (f) значения функции f(x), вызванную ошибкой задания ее аргумента.

Рассмотрим для определенности случай а < а*, когда приближенное значение превышает точное и применим к функции f(x),на отрезке [а, а*] формулу конечных приращений или теорему Лагра́нжа о среднем значении [], которая утверждает, что если функция f непрерывна на отрезке [a; а*] и дифференцируема в интервале (a; а*) (т.е. в любой точке интервала существует конечная или бесконечная производная), то всегда найдётся такая средняя точка b интервала (b (a; а*)), для которой выполняется равенство:

(f(а*) - f(а))/(а* - а) = f(b)). (2.11)

Геометрический смысл формулы заключается в том, что у дифференцируемой во всех точках интервала (a; а*) функции f(x) всегда найдется точка b, в которой угол наклона касательной к графику равен углу наклону отрезка, соединяющего начальную (a;f(а)) и конечную (a*;f(а*)) точки графика (рис.2.1). Если функция недифференцируема хотя бы в одной точке (х=с, рис.2.2), то такой точки может не быть.

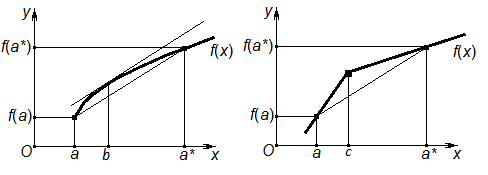
Рис.2.1.Дифференцируемая функция Рис.2.2. Недифференцируемая функция

В формуле (2.11) величина (f(а*) - f(а)) равна ошибке значения функции, вызванной погрешностью задания аргумента. Умножая обе части (2.11) на (а* - а) и переходя к модулям выражений, с учетом (а^) =а - а* получим:

f(а*) - f(а) = f(b)а* - а = f(b) (а^). (2.12)

Если вместо f(b) в формулу (2.12) подставить значение max(f(b)), в котором b (a; а*)), то для искомой предельной абсолютной погрешности (f) получим следующую оценку:

( f(а^) )  max(f(b))  (а^). (2.13)

В случае а > а* доказательство оценки выполняется аналогично. Отметим, что при заданном приближенном значении а^ возможное точное значение аргумента а может лежать на отрезке [а^ - (а^); а^ + (а^) ] . В случае, если задано точное значение х=а, то приближенном значении а^ может лежать на отрезке [а - (а^); а + (а^) ] .

Верхнюю оценку (2.13) назовем уточненной и обозначим (f(а^))_ут. Рассмотрим малые значения абсолютной погрешности аргумента. При (а^)0 величина max(f(b)) в пределе стремится к f(а). Подставляя ее в (2.13), получим приближенную оценку (обозначим ее (f(а^))_пр) для предельной абсолютной погрешности (f(а^)):

(f(а^)) f(а) (а^) = (f(а^))_пр. (2.14)

Из (2.14) можно найти приближенную оценку для предельной относительной погрешности значения функции (f(а)) = (f(а))/f(а) в зависимости от предельной относительной погрешности значения аргумента (а) = (а)/а:

(f(а))=(f(а))/f(а)(f(а)/f(а))а((а^)/а)=

=ln(f(а))а(а)/ =(f(а)) _пр. (2.15)

Как следует из полученных оценок (2.13) - (2.15), вычисление функции в точке с большим модулем первой производной может привести к значительному увеличению погрешности результата по сравнению с погрешностью аргумента.

Пример 1. Задана функция f(x) = х²+х-4 в точке x = а =-1 при заданной величине абсолютной погрешности аргумента (а^) = 0,1. Найти в заданной точке x =-1:

а) уточненное (f(-1))_ут и приближенное (f(-1))_пр значения предельной абсолютной погрешности функции,

б) приближенное (f(-1))_пр значение предельной относительной погрешности функции.

Решение. Первая производная функции f(x) = 2х+1. Модуль данной линейной функции является монотонной функцией, если на исследуемом отрезке она не меняет знак. Следовательно, при выполнении данного условия максимум f(х) достигается в какой-либо из крайних точек. Поскольку задано точное значение аргумента, то приближенное значение может лежать на отрезке [-1 - 0,1 = -1.1; -1 + 0,1 = -0.9]. Так как f(-1.1) = -1,2; f(-0.9) = -0,8; то max(f(b))=1,2 и из формулы (2.13) получим, что уточненное предельное значение абсолютной погрешности

(f(-1))_ут = 1,2  0,1 = 0,12.

Приближенное значение абсолютной погрешности находим по формуле (2.14) с учетом f (-1) = -1:

( f(-1) ) _пр = 1  0,1 = 0,1.

Предельную относительную погрешность значения функции находим по формуле (2.15) с учетом f(-1) = 1-1- 4 = -4 и (-1) = 0,1/1 = 0,1:

(f(-1)) _пр = (1/4) 10,1=0,025.