Из первых двух равенств находим:

Откуда или .

Из равенства следует, что знак нормирующего множителя противоположен знаку свободного члена С в общем уравнении прямой (3.11).

Пример 11. Привести общее уравнение прямой к нормальному виду.

Решение. Найдем нормирующий множитель по формуле (3.20):

.

Умножая данное уравнение на множитель , получим нормальное уравнение прямой:

.

2.3. Прямая на плоскости. Основные задачи

Угол между прямыми. Условия параллельности и перпендикулярности двух прямых. Пусть прямые и заданы уравнениями: а) с угловыми коэффициентами; б) общими уравнениями:

а) б)

: , ,

:

у

l₂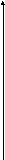

l₁

φ

В

α₂

α₁

х

О

А

С

Рис. 27

Найдем угол между прямыми (см. рис. 27).

а) Под углом между прямыми l₁ и l₂ понимаем такой угол , на который надо повернуть в положительном направлении прямую l₁ вокруг точки их пересечения В до совпадения с прямой l₂.

Пусть .

Так как (внешний угол треугольника АВС), то . Но , , поэтому

. (3.21)

Если требуется вычислить острый угол между прямыми, то

.

Б) в случае, когда прямые и заданы общими уравнениями, угол между прямыми можно определить как угол между нормальными векторами и этих прямых.

А именно,

(3.22)

Условие параллельности двух прямых l₁ и l₂ получается в случае: а) из формулы (3.21), при , б) из условия :

а) (3.23)

б) (3.24)

Условие перпендикулярности двух прямых l₁ и l₂ получается в случае: а) из формулы (3.21), при , б) из условия :

а) (3.25)

б) (3.26)

Пример 12. Найти угол между прямыми и .

Решение. Так как прямые заданы уравнениями с угловым коэффициентом и, . Поэтому по формуле (3.21), получим:

.

Таким образом, один из углов (острый) между прямыми , другой угол (тупой) равен .

Пример 13. Показать, что прямые и параллельны.

Решение. Так как прямые заданы общими уравнениями, то проверим условие (3.24): , где , .

Получим: или , следовательно, данные прямые параллельны.

Пример 14. Показать, что прямые и перпендикулярны.

Решение. Так как прямые заданы уравнениями с угловым коэффициентом, то проверим условие (3.25):

, где и .

Получим: , следовательно, данные прямые перпендикулярны.

Расстояние от точки до прямой. Пусть заданы прямая l уравнением и точка .

Расстояние d от точки до прямой l (рис. 28) равно модулю проекции вектора , где – произвольная точка прямой l на направлении нормального вектора .

у

l

d

М₀ (x₀,y₀)

М₁

О

х

Рис. 28

Следовательно,

Так как точка принадлежит прямой l, то , т.е. .

Поэтому расстояние от точки до прямой вычисляется по формуле:

. (3.27)

Другими словами, чтобы найти расстояние от точки до прямой, нужно в нормальное уравнение этой прямой подставить координаты данной точки и взять модуль полученного числа.

Пример 15. Найдите расстояние от точки до прямой .

Решение. Приведем уравнение прямой к общему виду:

.

Умножим обе части уравнения на 4, получим общее уравнение прямой . Теперь подставим координаты точки в формулу (3.27), где ,

.

Все основные формулы и утверждения, рассмотренные в этом параграфе, оформим в виде таблицы 3.

Таблица 3