1.2. Основные приложения метода координат на плоскости

Расстояние между двумя точками. Требуется найти расстояние между точками и плоскости .

Искомое расстояние равно длине вектора , т.е.

. (3.4)

Деление отрезка в данном отношении. Пусть в некоторой декартовой системе координат заданы три точки: , , , причем точка М делит отрезок М₁М₂ в отношении , т.е.

, или .

С учетом того, что координаты векторов

, ,

из последнего векторного равенства получим:

.

Отсюда найдем х, у:

(3.5)

– координаты точки М, делящей отрезок в данном отношении .

Если точка М – середина отрезка М₁М₂, то и координаты точки находят по формулам:

Замечание. Формулы (3.5) остаются справедливыми и для точек пространства, аналогичная формула записывается для координаты .

Пример 3. Даны точки и . Точка М делит отрезок М₁М₂ в отношении 3:2. Найдите координаты точки .

Решение. По условию . Из формулы (3.5) следует:

.

Следовательно, координаты точки .

Площадь треугольника. Площадь треугольника с вершинами в точках, , плоскости вычисляется через определитель второго порядка, по формуле

. (3.6)

Эту формулу можно получить непосредственно по чертежу, а также из формулы , где – векторное произведение векторов и (третьи координаты векторов равны нулю).

Пример 4. Найти площадь треугольника с вершинами , .

Решение. Подставим в формулу (3.6) координаты точек , получим:

1.3. Преобразования системы координат

Преобразованием системы координат называют переход от одной системы координат в какую-либо другую.

Рассмотрим два случая преобразования прямоугольной системы координат: параллельный перенос и поворот.

Параллельный перенос системы координат. Пусть на плоскости задана прямоугольная система координат.

Параллельный перенос системы координат – это такое преобразование системы координат Оху в новую систему координат О’х’у’, при котором меняется положение начала координат, а направление осей и масштаб остаются неизменными (рис. 17).

Пусть – начало новой системы координат и точка имеет координаты (х₀; у₀) в старой системе координат .

Обозначим координаты произвольной точки М плоскости в системе через (х; у), а в новой системе через (х_1;у₁);

y

М

y’

у₁

у₀

x'

y

x₁

О'

x₀

х

О

х

Рис. 17

Рассмотрим векторы , , .

По правилу сложения векторов имеем:

+ =

= .

Следовательно:

(3.7)

Формулы (3.7) называются формулами перехода от старых координат (х; у) к новым . Они позволяют находить старые координаты по известным новым, и наоборот.

Поворот системы координат. Поворот системы координат – это такое преобразование системы координат, при котором обе оси поворачиваются на один и тот же угол, а начало координат и масштаб остаются неизменными.

у

М

y’

у

x’

х₁

φ

у₁

α

О

х

х

Рис. 18

Пусть новая система координат получена поворотом системы на угол (рис. 18).

Пусть М – произвольная точка плоскости; – ее координаты в старой системе ; – ее координаты в новой системе .

Введем две полярные системы координат с общим полюсом и полярными осями и . Пусть масштаб будет в них одинаков. Тогда полярный радиус в обеих системах будет также одинаков, а полярные углы соответственно равны и , где – полярный угол в новой полярной системе.

По формулам перехода от полярных координат к прямоугольным имеем:

или

Но так как и , то

(3.8)

Формулы (3.8) называются формулами поворота системы координат.

Если новая система координат получена из старой системы с помощью параллельного переноса координатных осей и поворота осей на угол (см. рис. 19), то, используя формулы (3.7) и (3.8), получим следующие формулы преобразования координат:

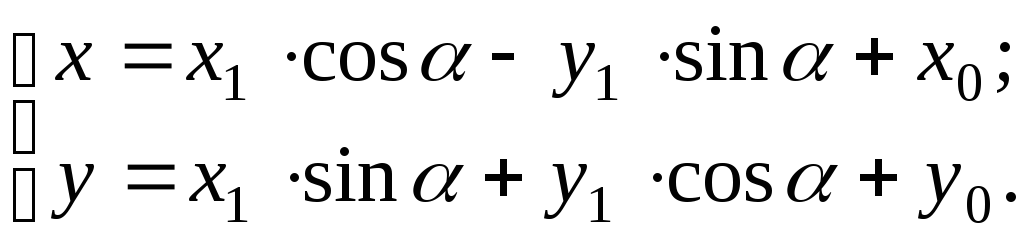(3.9)

y

у¹

α

О’

у₀

х¹

О

х

x₀

Рис. 19

Основные формулы и утверждения этого параграфа оформим в виде таблицы (см. табл. 2).

Таблица 2