Прямая в пространстве

Общее уравнение прямой	(1)
Канонические уравнения прямой	(2)
Переход от общего уравнения прямой (1) к каноническим уравнениям (2)	Найти точку Найти – направляющий вектор прямой как , где ,
Уравнение прямой через две данные точки
Параметрические уравнения прямой
Векторное уравнение прямой	= , где – направляющий вектор прямой

Угол между прямыми : : .
Условие параллельности двух прямых и
Условие перпендикулярности двух прямых и	m1 m2 + n1 n2 + p1 p2 = 0.
Условие принадлежности двух прямых и одной плоскости

6. Прямая и плоскость в пространстве основные задачи

Возможные случаи расположения прямой l и плоскости в пространстве:

1) Прямая l не лежит в плоскости , и тогда прямая l и плоскость могут:

а) пересекаться произвольным образом;

б) быть параллельными;

в) быть перпендикулярными.

2) Прямая l лежит в плоскости .

Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости. Пусть прямая l задана каноническим уравнением (3.48):

,

а плоскость – общим уравнением (3.39.):

Тогда – направляющий вектор прямой l, точка М₀ (х₀; у₀; z₀) , = (А, В, С) – нормальный вектор плоскости .

Пусть прямая l не лежит в плоскости .

Найдем угол между ними.

а) Углом между прямой l и плоскостью называют один из смежных углов, образованных прямой и ее проекцией на плоскость (рис. 39).

Пусть – угол между прямой l и плоскостью ; ψ – угол между векторами и = (А, В, С); φ = – ψ.

ψ φ α l Рис. 39

Так как ,

то ,

и тогда угол между прямой l и плоскостью вычисляется по формуле:

. (3.57)

б) Пусть прямая l параллельна плоскости . Тогда векторы

и =(А, В, С) перпендикулярны, и, следовательно, их скалярное произведение , т.е.

(3.58)

Уравнение (3.58) является условием параллельности прямой и плоскости.

в) Пусть прямая l перпендикулярна плоскости . Тогда векторы и = (А, В, С) колинеарны, а их координаты пропорциональны, т.е.

. (3.59)

Уравнения (3.58) являются условиями перпендикулярности прямой и плоскости.

Пересечение прямой с плоскостью. Условие принадлежности прямой плоскости. Пусть требуется найти точку пересечения прямой

с плоскостью .

Для этого запишем уравнения прямой в параметрическом виде:

Подставим эти выражения в уравнение плоскости, получим:

,

или

. (3.60)

1) Если прямая l не параллельна плоскости , т.е. если , то из равенства (3.59) находим значение :

.

2) Подставляя найденное значение параметра t в параметрические уравнения прямой, найдем координаты точки пересечения прямой l с плоскостью.

3. Если прямая l параллельна плоскости , т.е. если 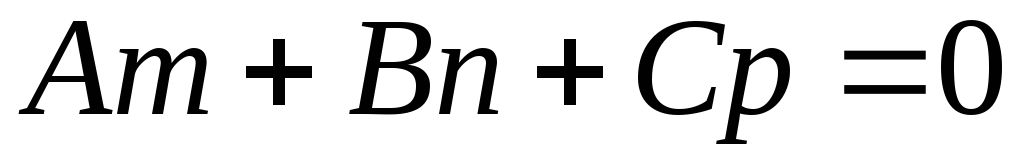, то в равенстве (3.60) возможны два случая:

а) , тогда уравнение (3.60) не имеет решения. Это означает, что прямая l параллельна плоскости и пересекать ее не будет;

б) , тогда уравнение (3.60) имеет вид и верно при любом значении . Это означает, что прямая l лежит в плоскости .

Таким образом, одновременное выполнение равенств

(3.61)

является условием принадлежности прямой плоскости.

Пример 23. Найдите точку пересечения прямой l:

и плоскости: .

Решение. 1) Прямая l задана каноническим уравнением. Приведем уравнение этой прямой к параметрическому виду:

,

2) Подставим полученные выражения для x, y, z в уравнение плоскости, тогда

,

откуда t = – 3.

3) Подставим найденное значение t = – 3 в параметрические уравнения прямой:

Таким образом, точка (0;0; –2) – точка пересечения прямой l и плоскости .

Пример 24. Составить уравнение плоскости , проходящей через прямую l₁:

,

параллельно прямой l₂:

.

Решение. Из заданных уравнений прямых имеем:

; ;

.

Пусть точка А (х; у; z) – произвольная точка плоскости , тогда вектор . Направляющие векторы прямых и вектор компланарны, тогда их смешанное произведение:

.