Часть 3 элементы аналитической геометрии

Аналитическая геометрия – это раздел геометрии, в котором геометрические объекты исследуются алгебраическими методами, основанными на методе координат.

Метод координат описал французский философ и математик Рене Декарт (1596–1650). А применение его к изучению пространственных линий и поверхностей впервые было сделано Леонардом Эйлером (1707–1783).

1. Системы координат на плоскости

1.1. Декартова и полярная системы координат на плоскости

В основе метода координат лежит понятие системы координат. Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки на плоскости.

Декартова система координат на плоскости. Декартова система координат (ДСК) – это две взаимно перпендикулярные оси и с выбранным положительным направлением и масштабом. Оси называют осями координат, – осью абсцисс, – осью ординат. Точка О пересечения осей и называется началом координат. Такую систему координат обозначают .

Координатами точки М в системе координат называются координаты радиус-вектора , и называются абсциссой и ординатой точки М соответственно. Точка М имеет координаты и обозначают как .

Эти два числа и полностью определяют положение точки на плоскости, а именно: каждой паре чисел и соответствует единственная точка плоскости, и наоборот.

Полярная система координат на плоскости. Полярная система координат на плоскости задается точкой , называемой полюсом, лучом , называемым полярной осью, и единичным вектором того же направления, что и луч (рис. 14).

Положение точки М в этой системе задается двумя числами: так называемым полярным радиусом и полярным углом , то есть углом между полярной осью и вектором .

Полярный угол измеряется в радианах и отсчитывается от полярной оси против часовой стрелки.

Точка М, заданная таким образом, имеет полярные координаты .

В полюсе , а угол  неопределенен. Для остальных точек плоскости , а изменение угла  ограничим пределами: .

Соотношения между декартовыми и полярными координатами. Совместим декартову систему координат на плоскости с полярной системой координат так, чтобы ось Ох совпала с полярной осью ОР, а начало координат – с полюсом (рис. 15).

Рис. 15

Пусть точка М в декартовой системе координат имеет координаты (х, у), а в полярной – .

Тогда:

(3.1)

, (3.2)

причем для однозначности определения угла  по его тангенсу надо учитывать знаки х и у.

Формулы (3.1) позволяют вычислить декартовы координаты точки по известным полярным координатам, а формулы (3.2) – наоборот, по известным декартовым координатам находят полярные.

Из формул (3.1) и (3.2) следует, что:

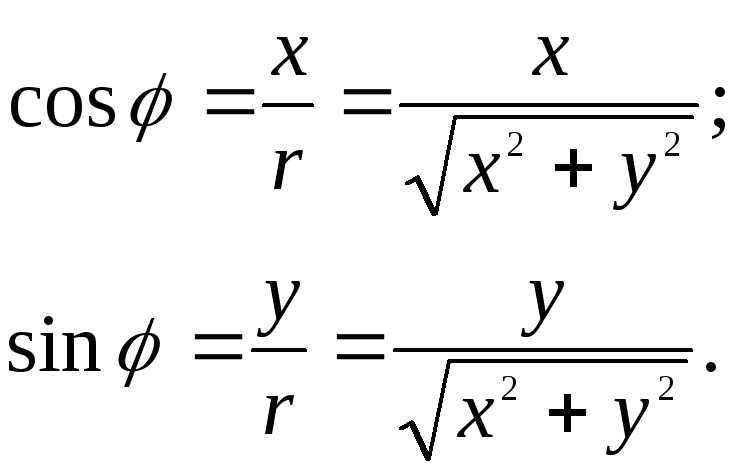(3.3)

Пример 1. В полярной системе координат требуется построить точки и .

Решение. Построение показано на рис. 16.

Проведем луч, образующий угол с полярной осью, и от полюса отложим отрезок, длина которого равна 2. Конец отрезка – искомая точка А.

Аналогично, строим точку В, учитывая, что откладываемый на полярной оси отрезок равен 3.

Пример 2. В декартовой системе координат дана точка . Найдите координаты точки М в полярной системе координат.

Решение. Воспользуемся формулами (3.2):

Искомая точка М имеет координаты: .