
- •Е.В. Бондарева
- •I. Линейная алгебра
- •§ 1. Матрицы. Действия над матрицами
- •§ 2. Определители.
- •§3. Обратная матрица.
- •§4. Ранг матрицы.
- •§5. Системы линейных уравнений.
- •II. Элементы векторной алгебры
- •§6. Векторы. Линейные операции над векторами (задачи на построение)
- •§7. Скалярное произведение векторов. Проекция вектора на заданное направление.
- •§8. Векторное произведение векторов.
- •§9. Смешанное произведение векторов.
- •§10. Линейные пространства.
- •§11. Линейные преобразования, §12. Квадратичные формы.
- •III. Аналитическая геометрия.
- •§13. Простейшие задачи на плоскости.
- •§14. Уравнение прямой на плоскости.
- •§15. Кривые второго порядка.
§9. Смешанное произведение векторов.
-
Найти смешанное произведение векторов

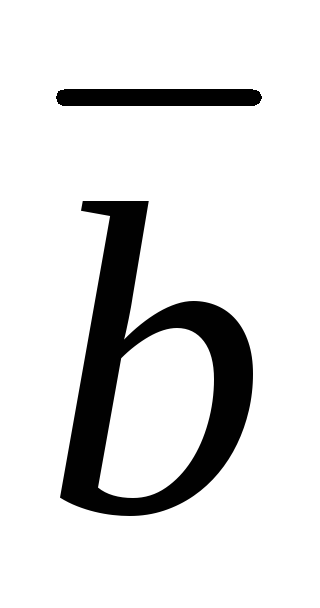
 ,
если:
,
если:
|
1)
2)
|
3)
|
2. Доказать, что векторы компланарны, если:
|
1)
2)
|
3)
|
3. Вычислить объем тетраэдра с вершинами в точках
1) А (–1; 1; 0); В (2; – 2; 1); С(3; 1; –1); D(1; 0; –2);
2) А (–4; – 4; – 3); В (– 2; –1; 1); С(2; – 2; –1); D(– 1; 3; –2)
4. Показать, что точки А (3; 5; – 4); В (1; –1; – 3); С(7; 2; –6); D(– 1; 3; –2)
принадлежат одной плоскости.
5.
Вычислить объем параллелепипеда,
построенного на векторах
![]() =(3;
2; 1);
=(3;
2; 1);
![]() =(1;
0; – 1);
=(1;
0; – 1);
![]() =(1;
–2; 1);
=(1;
–2; 1);
§10. Линейные пространства.
1. Выяснить, являются ли векторы а1, а2, а3 линейно зависимыми:
1) а1= (2; −1; 3), а2 = (1; 4; −1), а3= (0; −9; 5);
2) а1= (1; 2; 0), а2 = (3; −1; 1), а3= (0; 1; 1).
2. Показать, что векторы а1= (8; 5; 9; 1), а2 = (1; −3; –6; –3), а3= (3; –1; 5; 2), а4= (0; 2; –1; 4), заданные в базисе е1, е2, е3, сами образуют базис.
3. Даны векторы а = е1 + е2 + е3, b = 2е2 + 3е3, c = е2 + 5е3, где е1, е2, е3 базис линейного пространства. Доказать, что векторы a, b, c образуют базис. Найти координаты вектора d = 2е1 − е2 + е3 в базисе a, b, c.
4. Даны векторы а1, а2, а3, b. Показать, что векторы а1, а2, а3 образуют базис трехмерного пространства, и найти координаты вектора b в этом базисе, если:
1) а1= (4; 3; 2), а2 = (−3; 2; −1), а3 = (2; 3; 1), b=(16; 8; 7);
2) а1= (−1; 2; 0), а2 = (2; 4; 2), а3 = (−3; −1; 3), b=(−8; 0; 4).
5. Даны векторы а1, а2, а3, а4, b. Показать, что векторы а1, а2, а3, а4 образуют базис четырехмерного пространства, и найти координаты вектора b в этом базисе, если:
1) а1=(–1; 2; 3; 1), а2=(–1; 3;−2; –1), а3=(3; 5; 4; 1), а4=(3;1;4;–1), b=(0; 3; 5; 4);
2) а1=(1; 2; 1; 3), а2 =(1;–1;–1;–1), а3=(–1; 3; 0;1), а4 =(1;– 2; 2;–1), b=(4; 1; 6; 0).
Индивидуальное задание №2 по теме: «Элементы векторной алгебры»
Задание №1. Даны координаты вершин пирамиды ABCD. Требуется:
1.
Записать векторы
![]() ,
,
![]() ,
,
![]() в системе орт
в системе орт
![]() ,
,![]() ,
,
![]() и найти модули этих векторов;
и найти модули этих векторов;
2.
Найти угол между векторами
![]() и
и
![]() ;
;
3.
Найти
проекцию вектора
![]() на вектор
на вектор
![]() ;
;
4. Найти площадь грани АВС;
5. Найти объем пирамиды АВСD.
-
А(1; 2; 1), В( – 1; 5; 1), С( – 1; 2; 7), D (1; 5; 9).
-
А(2; 3; 2), В(0; 6; 2), С(0; 3; 8), D (2; 6; 10).
-
А(0; 3; 2), В( –2; 6; 2), С( – 2; 3; 8), D (0; 6; 10).
-
А(2; 1; 2), В(0; 4; 2), С( 0; 1; 8), D (2; 4; 10).
-
А(2; 3; 0), В( 0; 6; 0), С(0; 3; 6), D (2; 6; 8).
-
А(2; 2; 1), В(0; 5; 1), С(0; 2; 7), D (2; 5; 9).
-
А(1; 3; 1), В( – 1; 6; 1), С( – 1; 3; 7), D (1; 6; 9).
-
А(1; 2; 2), В( – 1; 5; 2), С( – 1; 2; 8), D (1; 5; 10).
-
А(2; 3; 1), В(0; 6; 1), С( 0; 3; 7), D (2; 6; 9).
-
А(2; 2; 2), В(0; 5; 2), С( 0; 2; 8), D (2; 5; 10).
-
А(1; 3; 2), В( – 1; 6; 2), С( – 1; 3; 8), D (1; 6; 10).
-
А(0; 1; 2), В( – 2; 4; 2), С( – 2; 1; 8), D (0; 4; 10).
-
А(0; 3; 0), В( – 2; 6; 0), С( – 2; 3; 6), D (0; 6; 8).
-
А(2; 1; 0), В( 0; 4; 0), С( 0; 1; 6), D (2; 4; 8).
-
А(0; 2; 1), В( – 2; 5; 1), С( – 2; 2; 7), D (0; 5; 9).
-
А(1; 1; 1), В( – 1; 4; 1), С( – 1; 1; 7), D (1; 4; 9).
-
А(1; 2; 0), В( – 1; 5; 0), С( – 1; 2; 6), D (1; 5; 8).
-
А(0; 1; 0), В( – 2; 4; 0), С( – 2; 1; 6), D (0; 4; 8).
-
А(0; 1; 1), В( – 2; 4; 1), С( – 2; 1; 7), D (1; 4; 9).
-
А(0; 2; 0), В( – 2; 5; 0), С( – 2; 2; 6), D (0; 5; 8).
-
А(4; 2; 5), В(0; 7; 2), С( 0; 2; 7), D (1; 5; 0).
-
А(4; 4; 10), В(4; 10; 2), С(2; 8; 4), D (9; 6; 4).
-
А(4; 6; 5), В(6; 9; 4), С(2; 10; 10), D (7; 5; 9).
-
А(3; 5; 4), В(8; 7; 4), С(5; 10; 4), D (4; 7; 8).
-
А(10; 6; 6), В( – 2; 8; 2), С(6; 8; 9), D (7; 10; 3).
-
А(1; 8; 2), В(5; 2; 6), С(5; 7; 4), D (4; 10; 9).
-
А(6; 6; 5), В(4; 9; 5), С(4; 6; 11), D (6; 9; 3).
-
А(7; 2; 2), В(5; 7; 7), С(5; 3; 1), D (2; 3; 7).
-
А(8; 6; 4), В(10; 5; 5), С(5; 6; 8), D (8; 10; 7).
-
А(7; 7; 3), В(6; 5; 8), С(3; 5; 8), D (8; 4; 1).
Задание
№2 Даны
векторы
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Показать, что векторы
.
Показать, что векторы
![]() ,
,
![]() ,
,
![]() образуют базис трехмерного пространства
и найти координаты вектора
образуют базис трехмерного пространства
и найти координаты вектора
![]() в этом базисе.
в этом базисе.
-
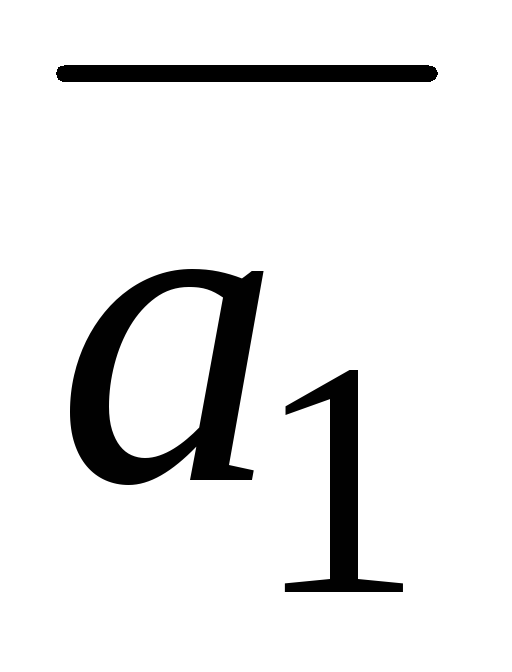 =(2;1;3),
=(2;1;3),
 =(3;
−2;1),
=(3;
−2;1),
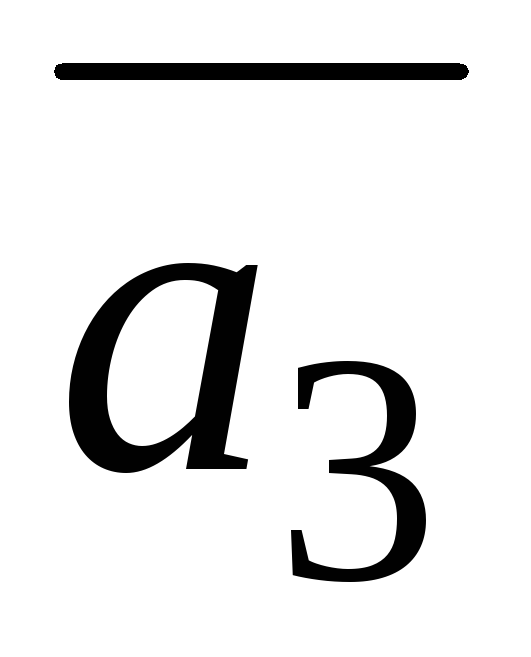 =(1;
−3; −4),
=(1;
−3; −4),
 =(7;0;7).
=(7;0;7). -
 =(5;3;1),
=(5;3;1),
 =(−2;
−1;2),
=(−2;
−1;2),
 =(−2;1;
4),
=(−2;1;
4),
 =(3;0;1).
=(3;0;1). -
 =(1;3;5),
=(1;3;5),
 =(−2;−1;−1),
=(−2;−1;−1),
 =(4;
−2;4),
=(4;
−2;4),
 =(−7;3;−1).
=(−7;3;−1). -
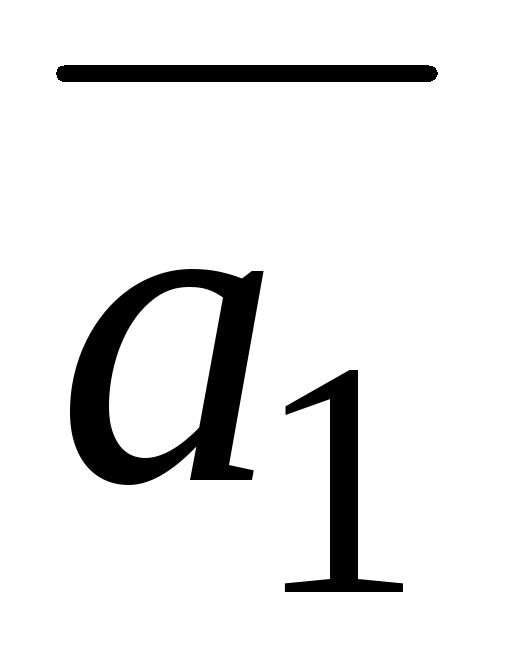 =(3;1;6),
=(3;1;6),
 =(−2;
2;−3),
=(−2;
2;−3),
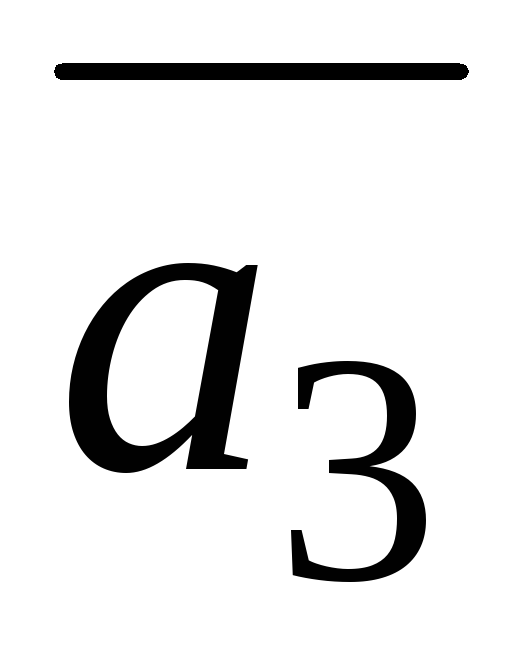 =(−4;
5; −1),
=(−4;
5; −1),
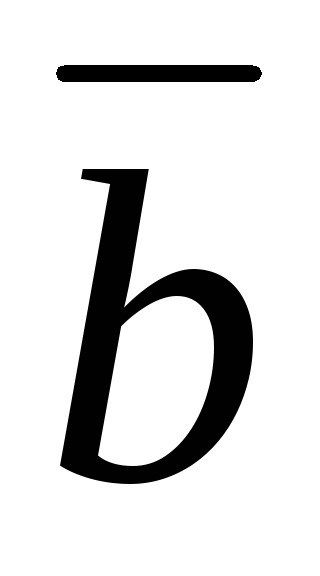 =(3;0;1).
=(3;0;1). -
 =(4;1;4),
=(4;1;4),
 =(−2;
−1;1),
=(−2;
−1;1),
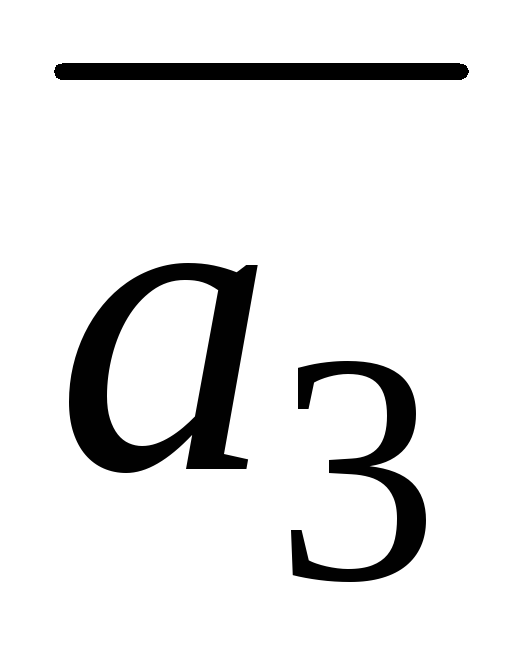 =(3;1;
5),
=(3;1;
5),
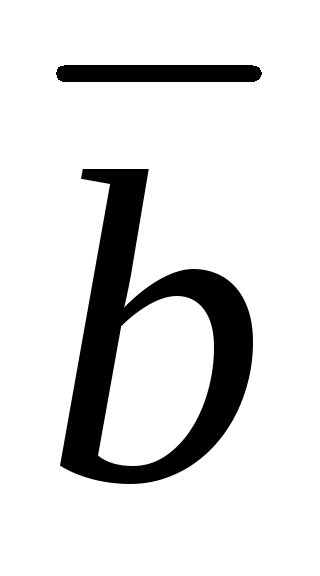 =(−
3;−2;1).
=(−
3;−2;1). -
 =(1;2;5),
=(1;2;5),
 =(2;
−3;4),
=(2;
−3;4),
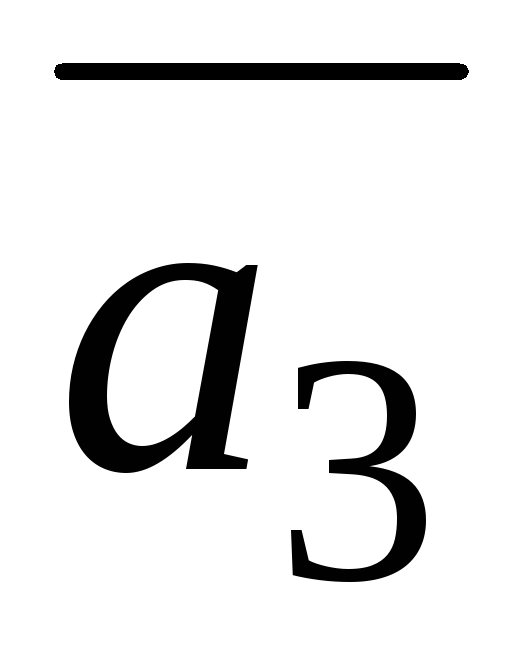 =(1;
−1; −2),
=(1;
−1; −2),
 =(3;0;1).
=(3;0;1). -
 =(5;1;2),
=(5;1;2),
 =(3;
4;−1),
=(3;
4;−1),
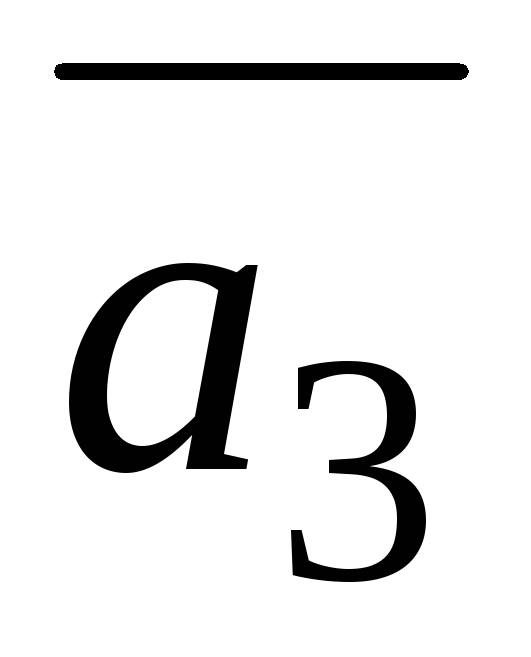 =(−4;
2; 1),
=(−4;
2; 1),
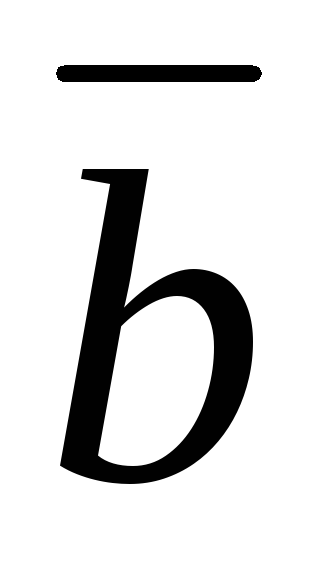 =(−3;5;4).
=(−3;5;4). -
 =(2;1;5),
=(2;1;5),
 =(−4;
3;5),
=(−4;
3;5),
 =(1;
−1; −4),
=(1;
−1; −4),
 =(4;−1;−3).
=(4;−1;−3). -
 =(3;1;4),
=(3;1;4),
 =(−4;2;3),
=(−4;2;3),
 =(2;−1;−2),
=(2;−1;−2),
 =(7;−1;0).
=(7;−1;0). -
 =(1;4;2),
=(1;4;2),
 =(5;−2;−3),
=(5;−2;−3),
 =(−2;−1;1),
=(−2;−1;1),
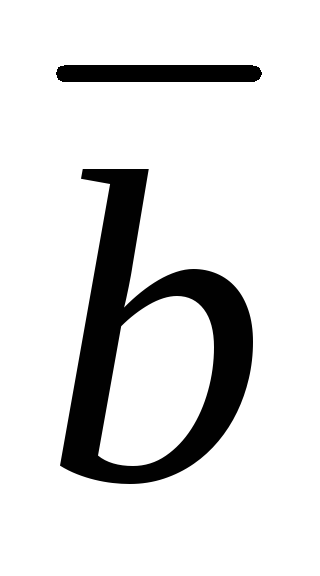 =(−3;2;4).
=(−3;2;4). -
 =(1;3;1),
=(1;3;1),
 =(1;
2;−1),
=(1;
2;−1),
 =(−3;
2;5),
=(−3;
2;5),
 =(0;−1;−2).
=(0;−1;−2). -
 =(3;1;5),
=(3;1;5),
 =(−2;3;−2),
=(−2;3;−2),
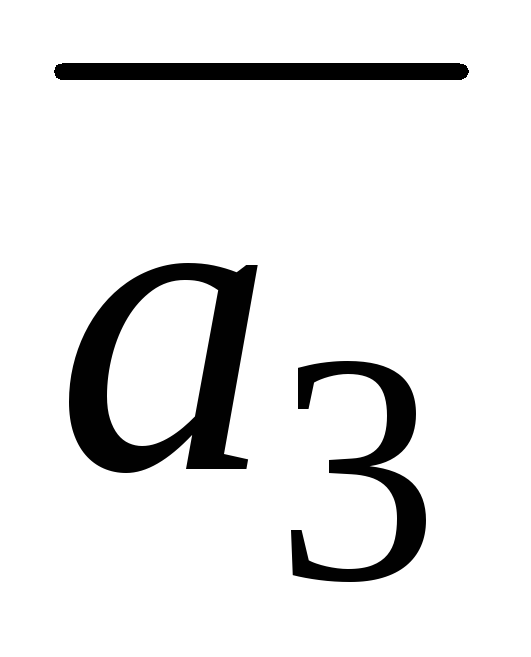 =(−1;
2; 4),
=(−1;
2; 4),
 =(−5;2;−7).
=(−5;2;−7). -
 =(2;1;4),
=(2;1;4),
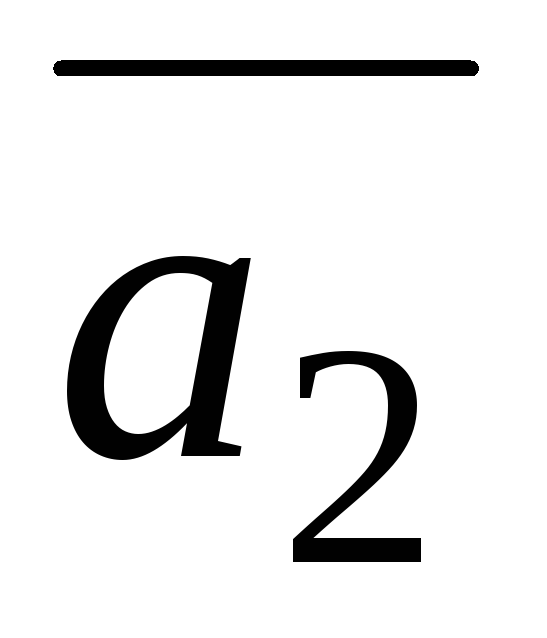 =(3;
1;5),
=(3;
1;5),
 =(1;
−4;−3),
=(1;
−4;−3),
 =(1;0;1).
=(1;0;1). -
 =(1;4;2),
=(1;4;2),
 =(−4;
1;3),
=(−4;
1;3),
 =(2;−3;4),
=(2;−3;4),
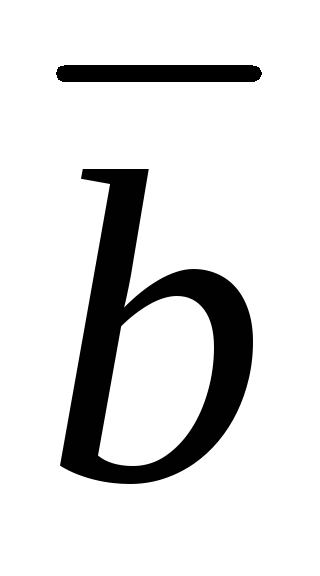 =(−5;−3;1).
=(−5;−3;1). -
 =(2;1;3),
=(2;1;3),
 =(4;
1;−2),
=(4;
1;−2),
 =(−3;2;1),
=(−3;2;1),
 =(2;0;−5).
=(2;0;−5). -
 =(1;2;4),
=(1;2;4),
 =(2;
−3;1),
=(2;
−3;1),
 =(−3;
−1; −2),
=(−3;
−1; −2),
 =(1;−7;0).
=(1;−7;0). -
 =(3;1;5),
=(3;1;5),
 =(−1;
2;3),
=(−1;
2;3),
 =(4;
3; 2),
=(4;
3; 2),
 =(2;7;8).
=(2;7;8). -
 =(3;2;1),
=(3;2;1),
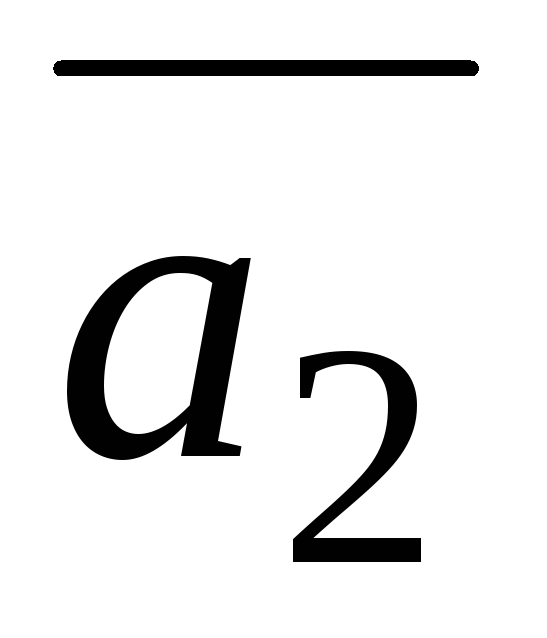 =(−3;1;−2),
=(−3;1;−2),
 =(2;3;5),
=(2;3;5),
 =(−4;−1;1).
=(−4;−1;1). -
 =(4;3;2),
=(4;3;2),
 =(−1;
2;−2),
=(−1;
2;−2),
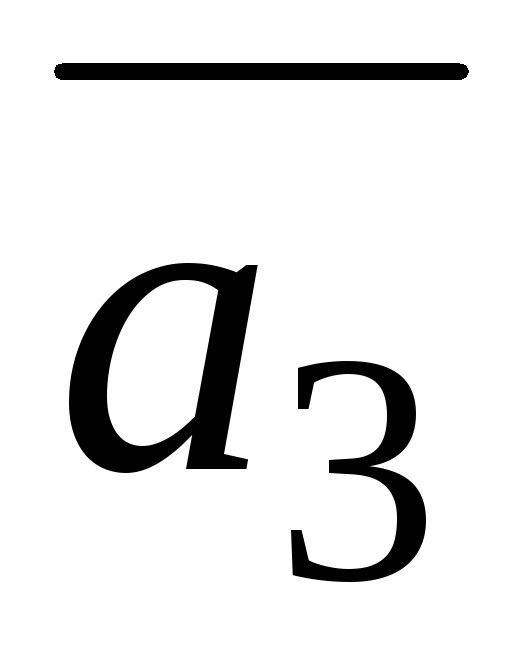 =(3;4;4),
=(3;4;4),
 =(1;8;0).
=(1;8;0). -
 =(2;1;4),
=(2;1;4),
 =(−1;−2;3),
=(−1;−2;3),
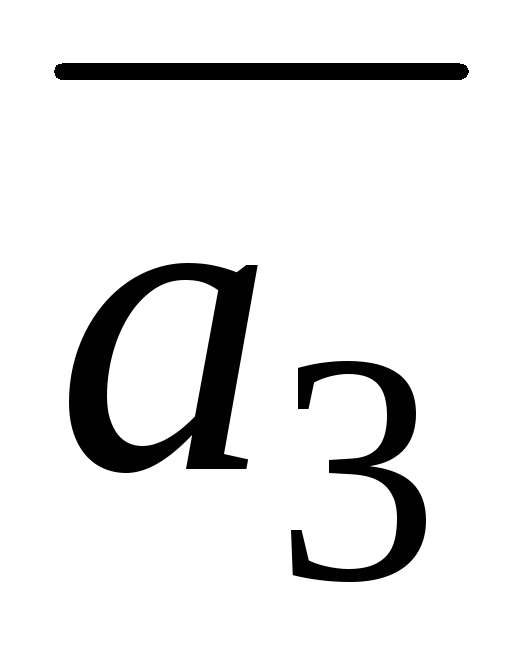 =(3;
−5; −2),
=(3;
−5; −2),
 =(1;−9;4).
=(1;−9;4). -
 =(5;1;2),
=(5;1;2),
 =(8;2;−3),
=(8;2;−3),
 =(−1;3;2),
=(−1;3;2),
 =(−7;1;9).
=(−7;1;9). -
 =(1;3;2),
=(1;3;2),
 =(2;
−5;7),
=(2;
−5;7),
 =(1;3;−1),
=(1;3;−1),
 =(4;1;8).
=(4;1;8). -
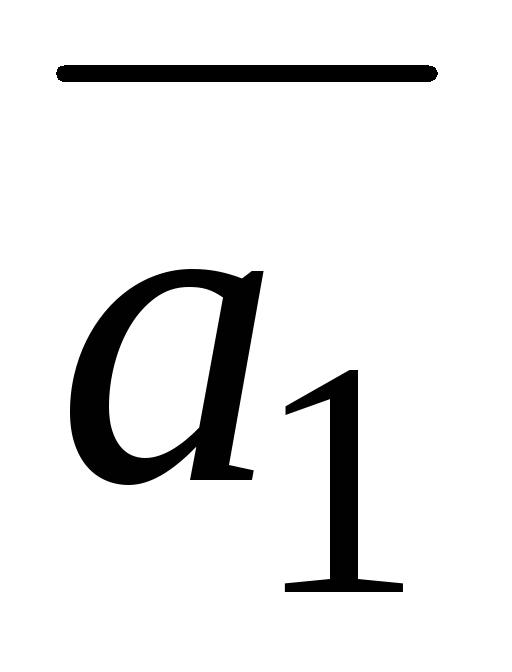 =(3;2;2),
=(3;2;2),
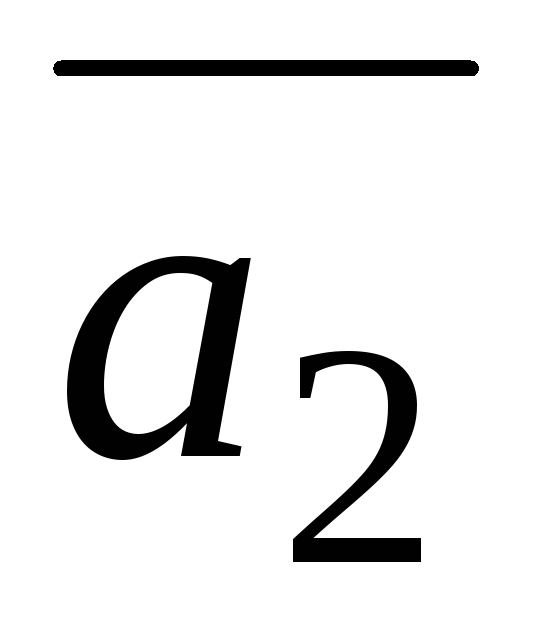 =(2;3;1),
=(2;3;1),
 =(1;
1; 3),
=(1;
1; 3),
 =(5;1;11).
=(5;1;11). -
 =(1;5;3),
=(1;5;3),
 =(2;1;−1),
=(2;1;−1),
 =(4;2;1),
=(4;2;1),
 =(31;29;10).
=(31;29;10). -
 =(4;2;5),
=(4;2;5),
 =(−3;5;6),
=(−3;5;6),
 =(2;−3;−2),
=(2;−3;−2),
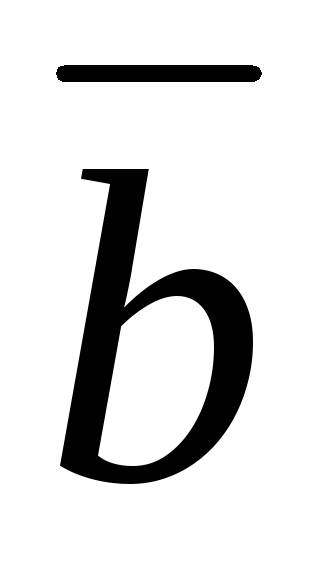 =(9;4;18).
=(9;4;18). -
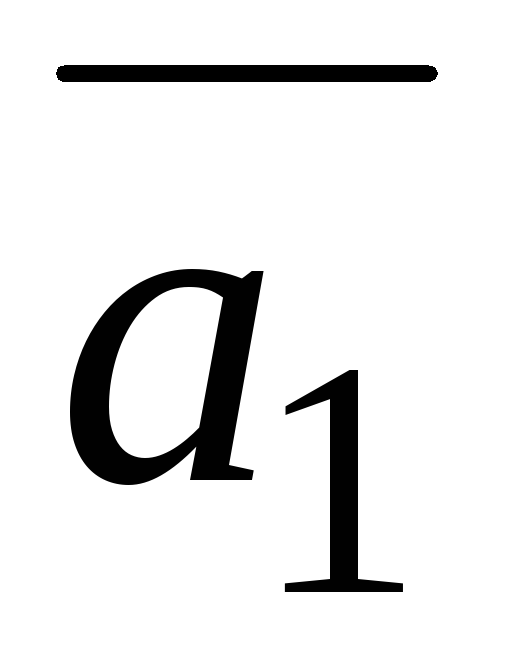 =(2;3;3),
=(2;3;3),
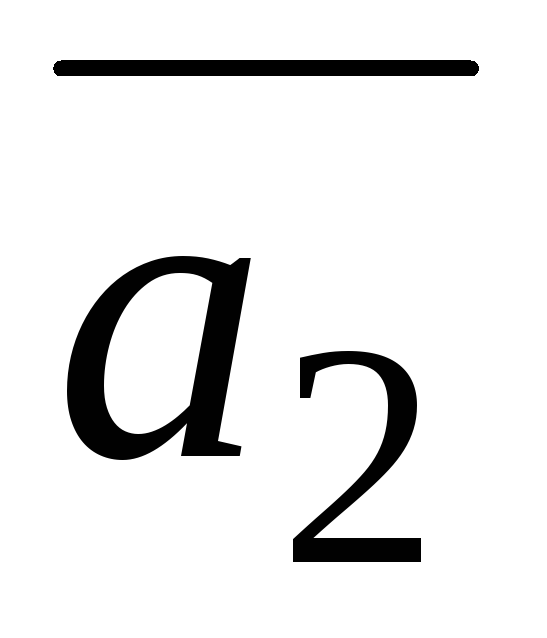 =(−1;4;−2),
=(−1;4;−2),
 =(−1;−2;4),
=(−1;−2;4),
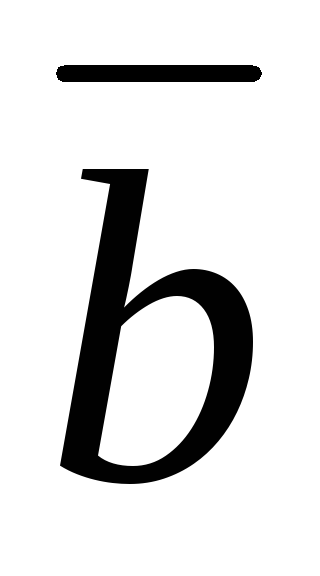 =(4;11;11).
=(4;11;11). -
 =(1;2;4),
=(1;2;4),
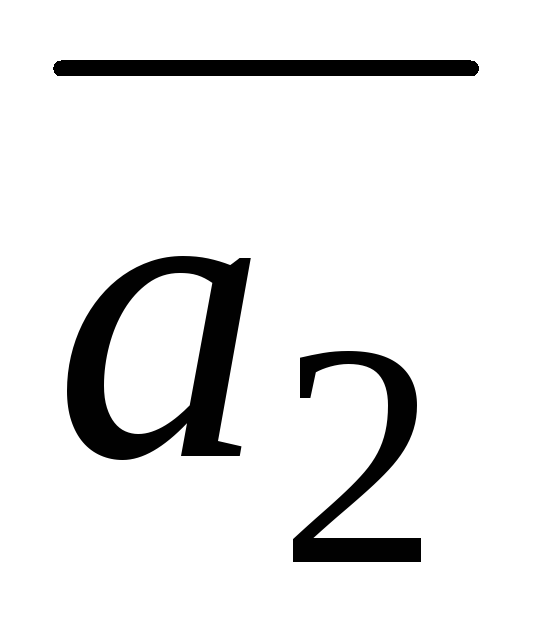 =(1;−1;1),
=(1;−1;1),
 =(2;2;4),
=(2;2;4),
 =(−1;−4;−2).
=(−1;−4;−2). -
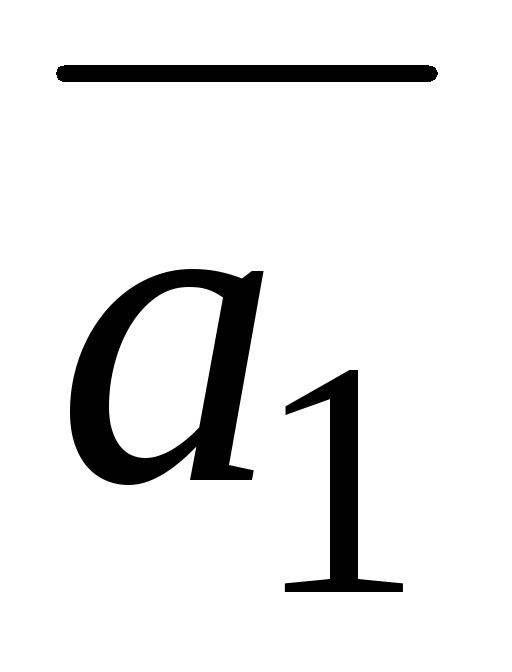 =(3;−2;2),
=(3;−2;2),
 =(−1;1;−1),
=(−1;1;−1),
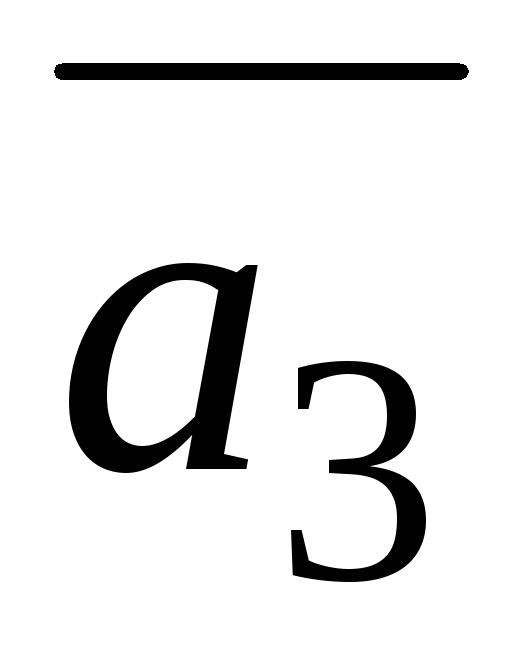 =(0;1;4),
=(0;1;4),
 =(5;0;15).
=(5;0;15). -
 =(3;2;1),
=(3;2;1),
 =(−1;−5;1),
=(−1;−5;1),
 =(1;−3;−1),
=(1;−3;−1),
 =(4;−17;0).
=(4;−17;0). -
 =(1;2;3),
=(1;2;3),
 =(1;−1;−2),
=(1;−1;−2),
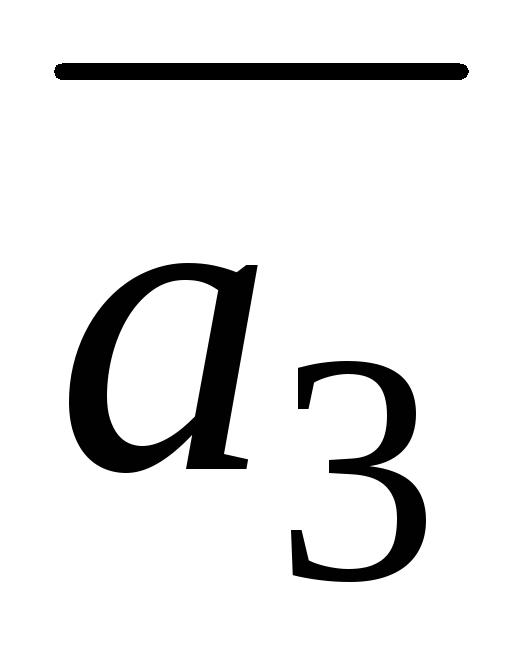 =(1;−6;0),
=(1;−6;0),
 =(−1;8;3).
=(−1;8;3).
