3. Теорема о движении центра масс механической системы

3.1 Дифференциальные уравнения движения механической системы

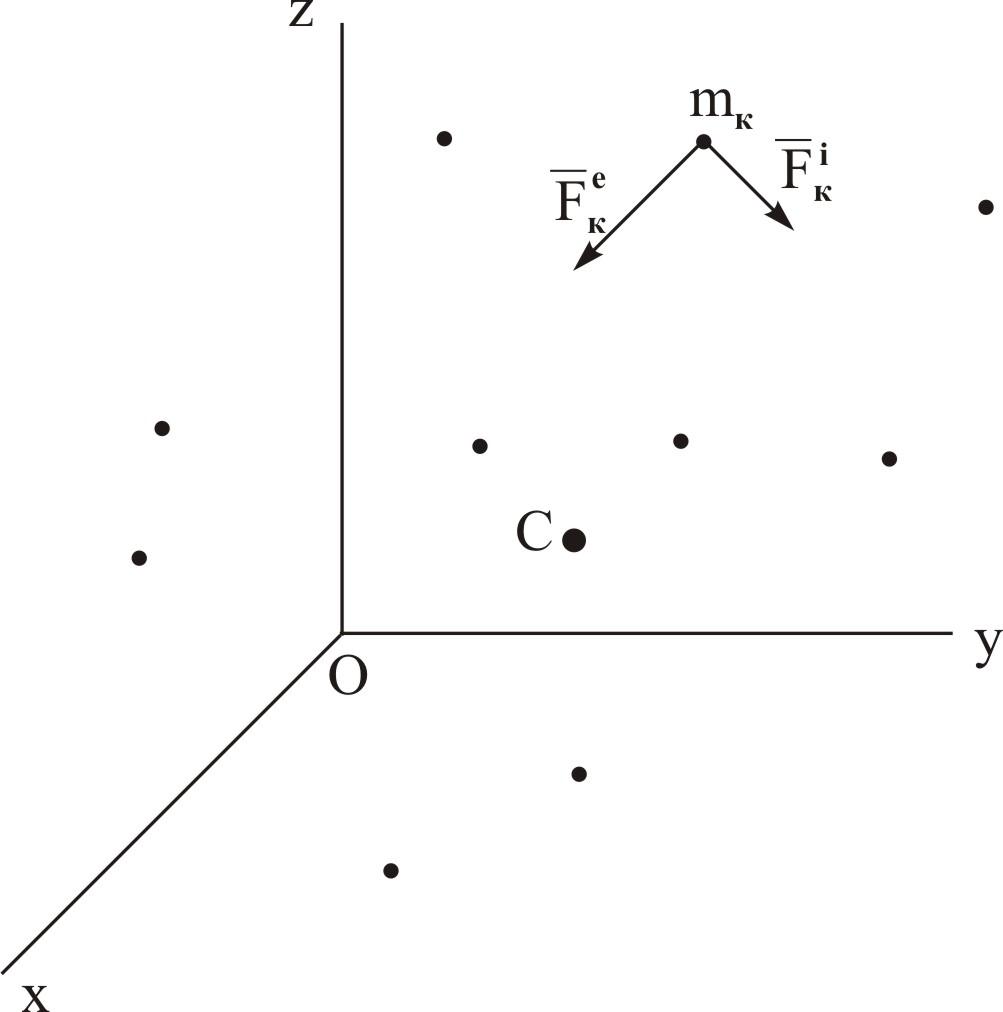Рассмотрим механическую систему, состоящую из n материальных точек. Выделим какую-нибудь точку системы с массой m_к. Обозначим равнодействующую всех приложенных к точке внешних сил (и активных реакций связей) через , а равнодействующую всех внутренних сил – через (рисунок 3.1). Если точка имеет при этом ускорение , то по основному закону динамики

. (3.1)

Уравнение (3.1) представляет собой дифференциальное уравнение движения к^й точки. Проецируя векторы обеих частей равенства (3.1) на оси х, у, z; получим дифференциальные уравнения движения системы в проекциях на эти оси:

Рисунок 3.1

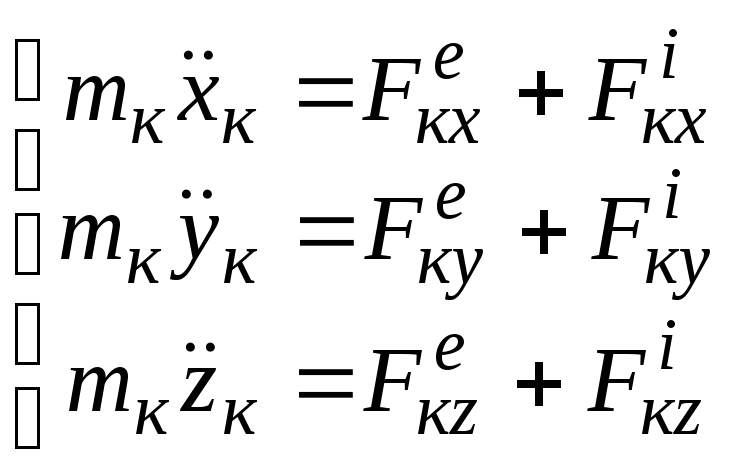. (3.2)

Для механической системы, имеющей n точек, получим 3n совместных дифференциальных уравнений движения. Так как внутренние силы, приложенные к точкам системы, в большинстве случаев остаются неизвестными, а число точек системы обычно велико, то эти 3n уравнений могут быть проинтегрированы лишь в исключительных случаях, поэтому используют другой способ для решения задач на движение системы тел.

3.2 Теорема о движении центра масс механической системы

В ряде случаев для определения характера движения системы (обычно твердого тела) требуется знать закон движения ее центра масс. Чтобы найти этот закон, составим уравнения движения для всех точек системы в виде (3.1) и сложим почленно их левые и правые части. Тогда получим:

(3.3^/)

преобразуем левую часть этого равенства. Из формулы (2.2.1) для радиуса-вектора центра масс имеем

.

Беря от обеих частей этого равенства вторую производную по времени и замечая, что производная от суммы равна сумме производных, найдем

или (3.3)

где - ускорение центра масс системы.

Так как по свойству внутренних сил системы , получим окончательно из равенства (3.3^/), учтя (3.3)

(3.4)

т.е. произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил.

Уравнение (3.4) выражает теорему о движении центра масс системы, которая формулируется следующим образом: центр масс механической системы движется как материальная точка массой, равной массе всей системы, к которой приложены все внешние силы, действующие на систему.

Проецируя обе части векторного равенства (3.4) на оси х,у,z, получаем три уравнения в проекциях на оси координат:

(3.5)

Уравнения (3.5) представляют собой дифференциальные уравнения движения центра масс. Из уравнений (3.4) и (3.5) следует, что внутренние силы непосредственно не влияют на движение центра масс, в связи с чем уравнения (3.4) и (3.5) имеют больше практическое значение.

Из кинематики известно, что поступательное движение твердого тела полностью определяется движением одной из его точек. Следовательно, решив задачу о движении центра масс тела как материальной точки массой, равной массе всего тела, можно определить поступательное движение всего тела.

Следствия из теоремы:

1. Если главный вектор внешних сил () остается все время равным нулю, то центр масс механической системы находится в покое или движется равномерно и прямолинейно.

Из (3.4) если , то , т.е. . При этом, если центра масс равна нулю, то центр масс находится в покое. Если же , то центр масс движется равномерно и прямолинейно с этой скоростью.

2. Если проекция главного вектора внешних сил на какую-либо неподвижную ось остается все время равной нулю, то проекция центра масс механической системы на эту ось неподвижна или движется равномерно, т.е. если , то , т.е. ; если , то и . Следствия из теоремы о движении центра масс системы выражают закон сохранения движения центра масс системы.

Вопросы для самоконтроля

1. Сформулируйте теорему о движении центра масс системы.

2. Какое движение твердого тела можно рассматривать как движение материальной точки, имеющей массу данного тела. Почему?

3. При каких условиях центр масс системы находится в состоянии покоя, и при каких условиях он движется равномерно и прямолинейно?

4. При каких условиях центр масс системы не перемещается вдоль некоторой оси?