Прямолинейное равноускоренное движение
1.4 Классификация движения точки по ее ускорениям
Классифицировать движение точки можно по-разному. Например, по траектории различают прямолинейное и криволинейное движение. По скоростям различают равномерное, равнопеременное и переменное движения.
Наиболее общей классификацией движения точки, которая охватывает и перечисленные классификации, является классификация по ускорениям точки. Как известно, в общем случае ускорение точки определяется по формуле
Рассмотрим частные случаи:
1. При движении точки ее нормальное
ускорение равно нулю, т.е. аn
= 0. Так как
,
то поскольку точка движется, т.е. v
≠ 0, то ρ =
,
т.е. точка движется прямолинейно.
Поскольку при прямолинейном движении
скорость точки не изменяется по
направлению, следовательно, нормальное
ускорение характеризует изменение
вектора скорости по направлению.
2. Очевидно, если нормальное ускорение точки не равно нулю ( аn ≠ 0 ), то точка движется по криволинейной траектории.
3. При движении точки ее тангенциальное
ускорение равно нулю, т.е. аτ=0,
поскольку аτ =
,
то
= 0, следовательно, vτ
= const.
Движение с постоянной по модулю скоростью
называется равномерным.
Следовательно, в данном случае при аτ=0
точка движется равномерно. Найдем
закон этого движения: т.к.
,
то
.
Интегрируя и считая, что vτ = const, получим
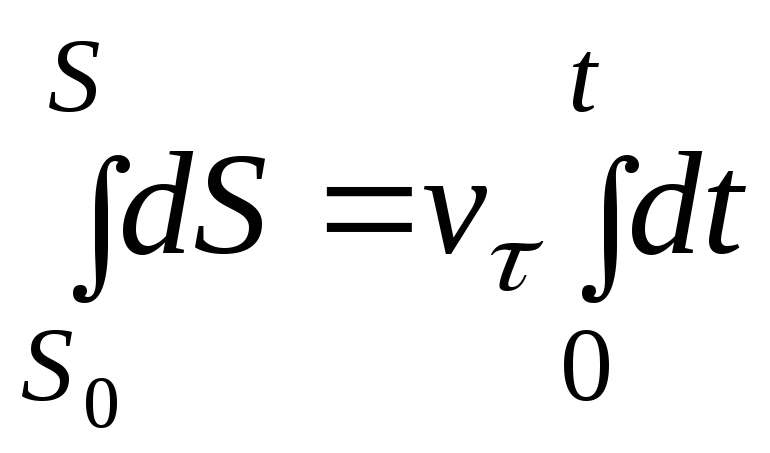или
S=S0 + vt ·t (А.1)
Формула (А.1) и представляет собой закон равномерного движения точки, где S0 – начальная дуговая координата, т.е. значение дуговой координаты в момент времени t = 0 (рисунок А.1).
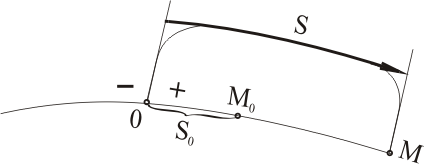
Рисунок А.1
Если точка движется в положительном направлении изменения дуговой координаты, то
S=S0 + v ·t. (А.2)
Если точка движется в отрицательном направлении изменения дуговой координаты, то
S=S0 – v ·t, (А.3)
где v – модуль постоянной скорости точки.
Таким образом, если скорость точки не изменяется по величине, то ее тангенциальное ускорение равно нулю, следовательно, тангенциальное ускорение характеризует изменение вектора скорости точки по величине.
4. Тангенциальное ускорение точки является постоянной величиной, не равной нулю, т.е. аτ = const ≠ 0. Движение с постоянным тангенциальным ускорением называется равнопеременным.
Так как
,
то
,
интегрируя, получим закон изменения
алгебраической скорости точки при
равнопеременном движении
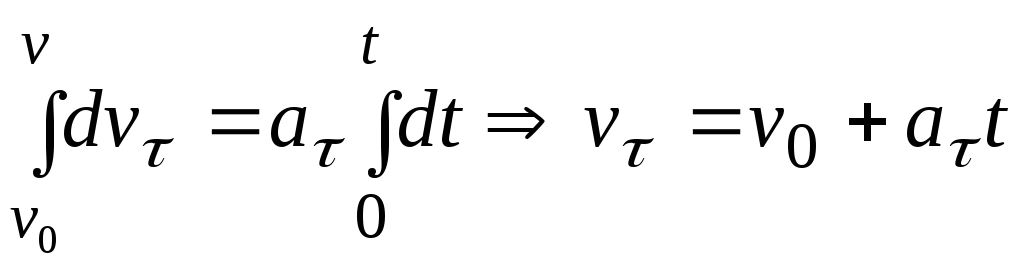, (А.4)
где v0 – начальная скорость точки.
Так как
,
то можно записать используя формулу
(А.1.4)
,
откуда, интегрируя, получим закон равнопеременного движения точки
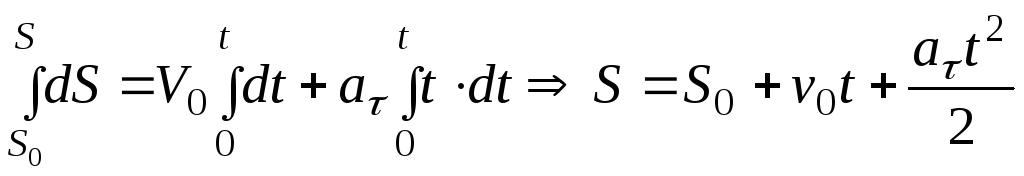(А.5)
где S0 – начальная дуговая координата точки.
Вопросы для самоконтроля
1. Назовите основные кинематические характеристики движения точки.
2. Какие движения может совершать точка?
3. Какими способами можно задавать движение точки?
4. Запишите уравнение движения точки в векторной форме.
5. Запишите уравнение движения точки в декартовой системе координат.
6. Запишите закон движения точки на траектории.
7. Движение точки определяется уравнениями
,
.
Найти уравнение траектории.
8. Точка движется по кругу радиусом 2 м с постоянной скоростью V=5 м/с. Каким способом задано уравнение движения точки.
9. Радиус – вектор точки изменяется по
закону
.
Запишите уравнения движения точки в
координатной форме.
10. Движение точки задано уравнениями
,
м,
,
м. Определите скорость точки.
11. Определите ускорение точки, движение
которой описывается уравнениями
,
м;
,
м.
12. Какие оси координат называются естественными?
13. Как называется, и по какой формуле определяется проекция ускорения на главную нормаль?
14. Как называется, и по какой формуле определяется проекция ускорения на касательную ось?
15. Чему равна проекция ускорения на бинормаль?
16. Как движется точка, если
а) аn = 0; aτ = 0
б) аn ≠ 0; aτ = 0
в) аn = 0; aτ = const ≠ 0
17. Какое движение точки называется равномерным?
18. Может ли иметь ускорение точка при равномерном движении.
19. Запишите уравнение равнопеременного движения точки.